Введение в частные производные для функций двух переменных
Эта страница предоставляет полезные советы и примеры для работы с частными производными функций двух переменных. Вы узнаете, как правильно вычислять частные производные, их применение в различных областях и как они могут помочь в решении задач в математике и смежных науках.


Изучите определение частных производных и их геометрическое представление для лучшего понимания их применения.

Частные производные функции многих переменных

Практикуйтесь на различных примерах, чтобы закрепить навыки вычисления частных производных функций двух переменных.

artimpression.ruе производные второго порядка сложной функции

Используйте графические методы и программы для визуализации изменений функции и ее частных производных.

6. Частные производные функции двух переменных


Обратите внимание на правила дифференцирования сложных функций, особенно при наличии нескольких переменных.
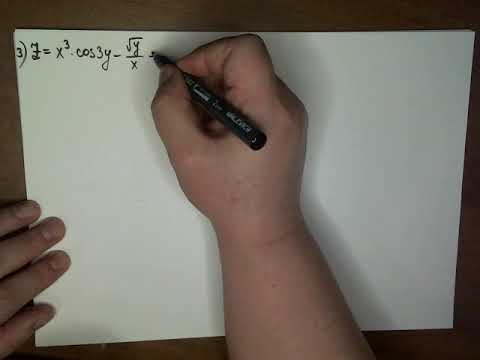
Частные производные первого и второго порядка от функций нескольких переменных

Рассмотрите примеры из реальных приложений, таких как физика или экономика, чтобы понять, как частные производные могут применяться в практике.

Смысл интеграла и производной. В помощь студенту


Понимание понятий локальных экстремумов и их связи с частными производными поможет в анализе функций.

Математический анализ, 29 урок, Функции нескольких переменных. Частные производные


Регулярно проверяйте свои вычисления и результаты, чтобы избежать ошибок в математических операциях.

8. Примеры решения частных производных №2


Используйте книги и онлайн-ресурсы для углубленного изучения методов и техник работы с частными производными.

9. Геометрический смысл частных производных функции двух переменных

Дифференцируемость в точке решение примеров
Обсуждайте трудные вопросы и задачи с коллегами или преподавателями для получения новых перспектив и решений.


Развивайте навыки работы с программами для вычисления и анализа частных производных, такими как MATLAB или Mathematica.


Математика без Ху%!ни. Частные производные функции нескольких переменных. Градиент.