Как определить чётные и нечётные функции: практическое руководство
В этой статье мы рассмотрим ключевые концепции чётности и нечётности функций, которые играют важную роль в математическом анализе и различных прикладных задачах. Узнайте, как распознать чётные и нечётные функции и как эти свойства могут быть полезны при решении математических задач.
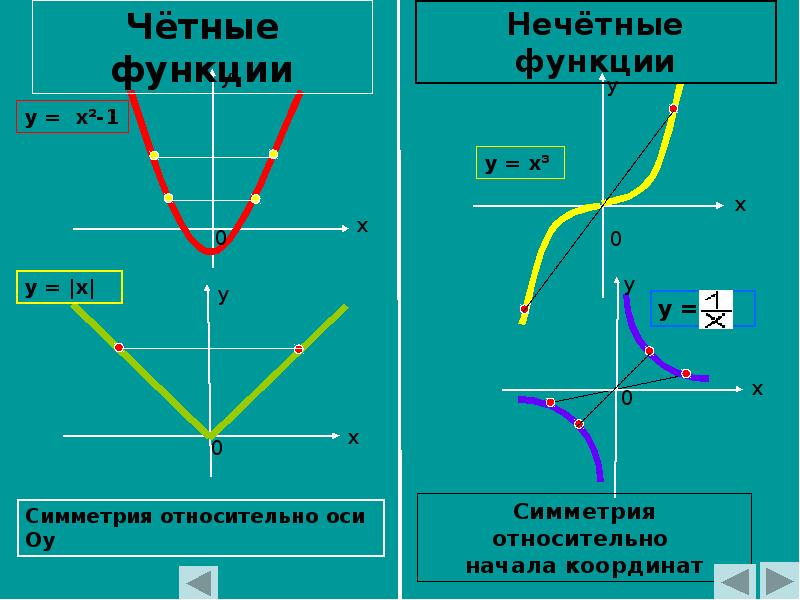
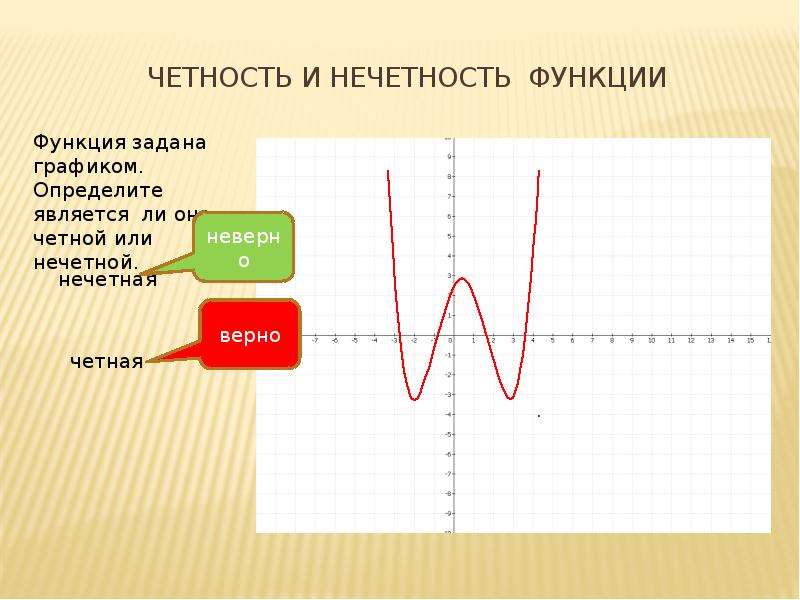

Чтобы проверить, является ли функция чётной, подставьте -x вместо x и посмотрите, равна ли функция исходному выражению. Если да, то функция чётная.

Чётность или нечётность функции

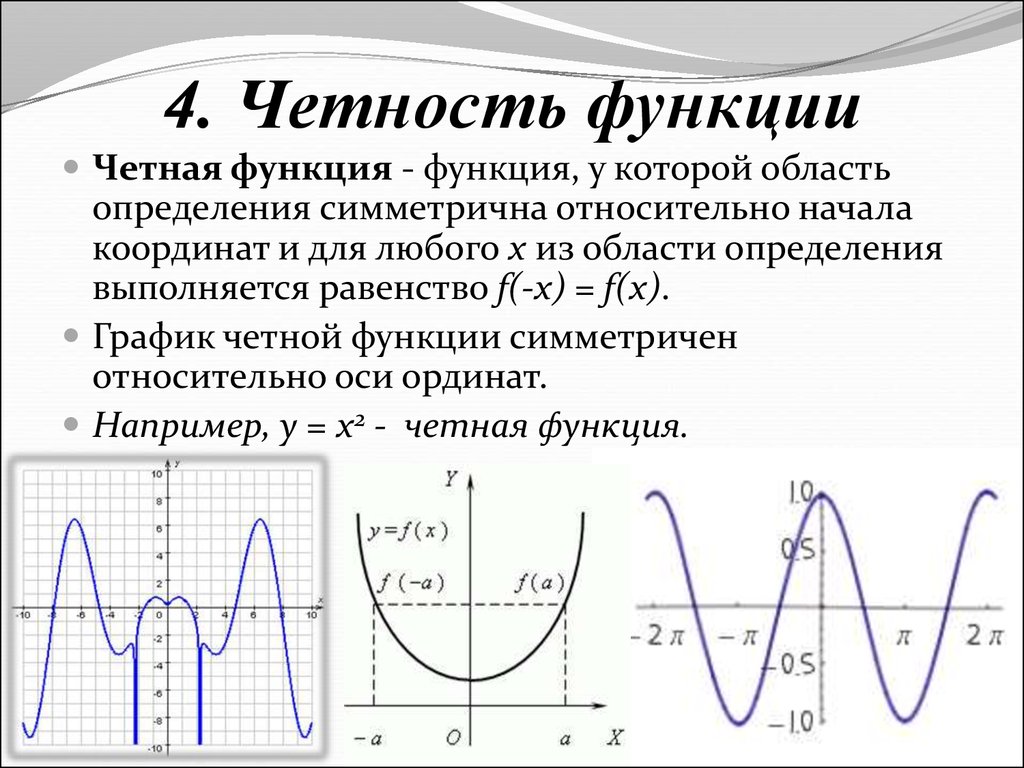
Для проверки нечётности функции, подставьте -x и проверьте, получается ли противоположное значение исходному выражению. Если это так, функция нечётная.

Чётность и нечётность функции - Математика
Функции вида f(x) = x^n, где n — четное число, являются чётными. Если n нечетное, функция нечётная.
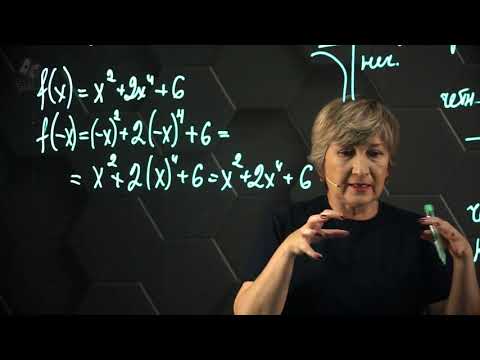
Свойства функции. Четность и нечетность функции. 10 класс.


Функции, содержащие синус и косинус, часто являются чётными или нечётными в зависимости от их аргументов и коэффициентов. Например, косинус — чётная функция, а синус — нечётная.

Четность или нечетность функции #5
Чтобы определить чётность или нечётность сложных функций, разложите их на простые функции и проанализируйте каждую по отдельности.
9 класс, 18 урок, Чётные и нечётные функции

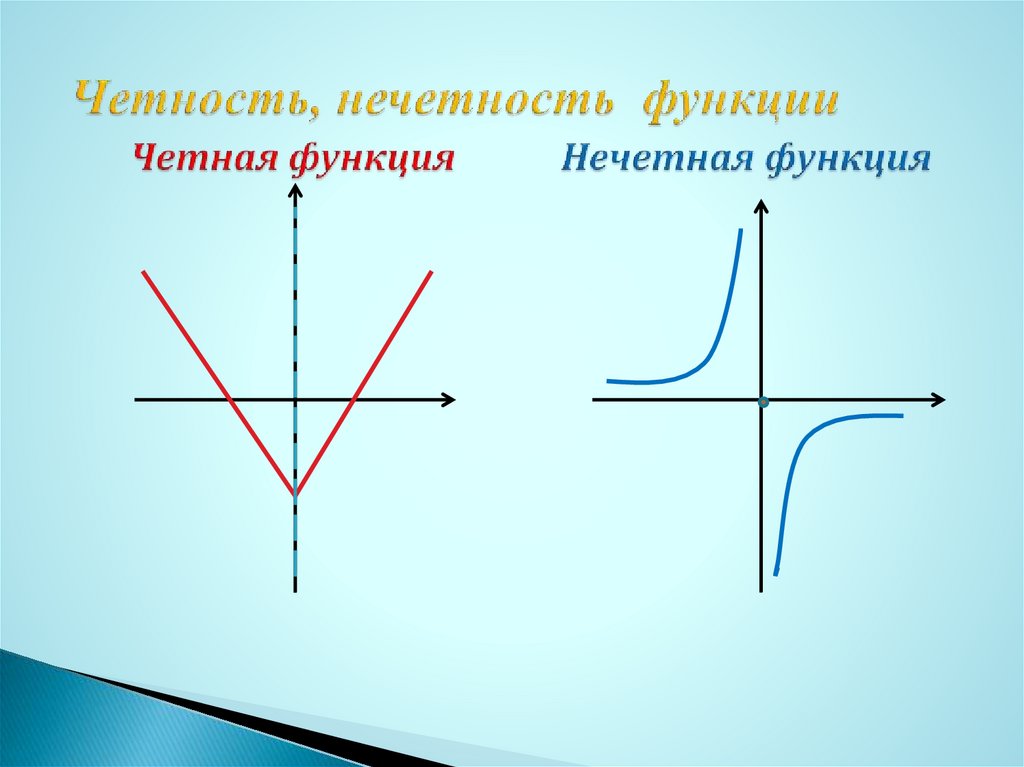
Функция может быть ни чётной, ни нечётной. Например, f(x) = x + 1 не является ни чётной, ни нечётной.

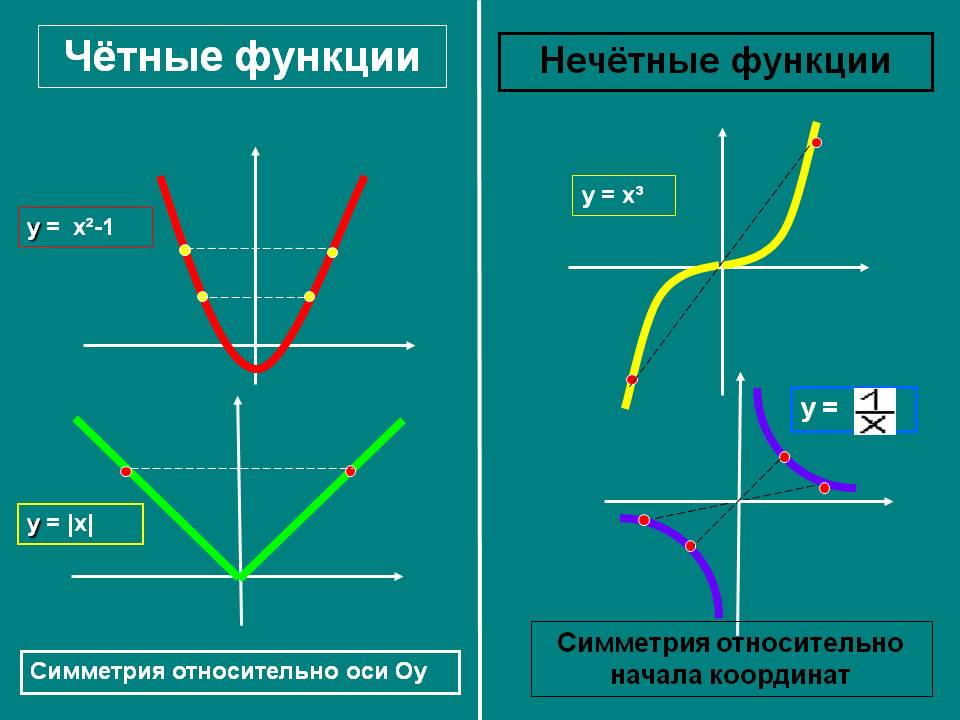
Используйте графический подход: чётные функции симметричны относительно оси y, а нечётные функции симметричны относительно начала координат.

Четность и нечетность тригонометрических функций (синус, косинус, тангенс и котангенс)

Для функции f(x) = x^3, график функции покажет симметрию относительно начала координат, что указывает на её нечётность.

ЧЕТНОСТЬ функции НЕЧЕТНОСТЬ функции
Если функция имеет составные выражения, попробуйте разложить её на суммы или произведения чётных и нечётных функций для упрощения анализа.

ВСЕ, ЧТО НУЖНО ЗНАТЬ ПРО ВИДЫ ФУНКЦИЙ — Четные и Нечетные Функции

При работе с функциями важно также учитывать области определения, так как чётность и нечётность могут быть ограничены этими областями.

Четность и нечетность функции