Как использовать свойства треугольников в геометрии на практике
В этой статье представлены полезные советы и примеры по работе с треугольниками, включая их свойства и способы применения в различных задачах. Узнайте, как правильно использовать данные о треугольниках для решения геометрических задач и улучшения своих навыков в математике.
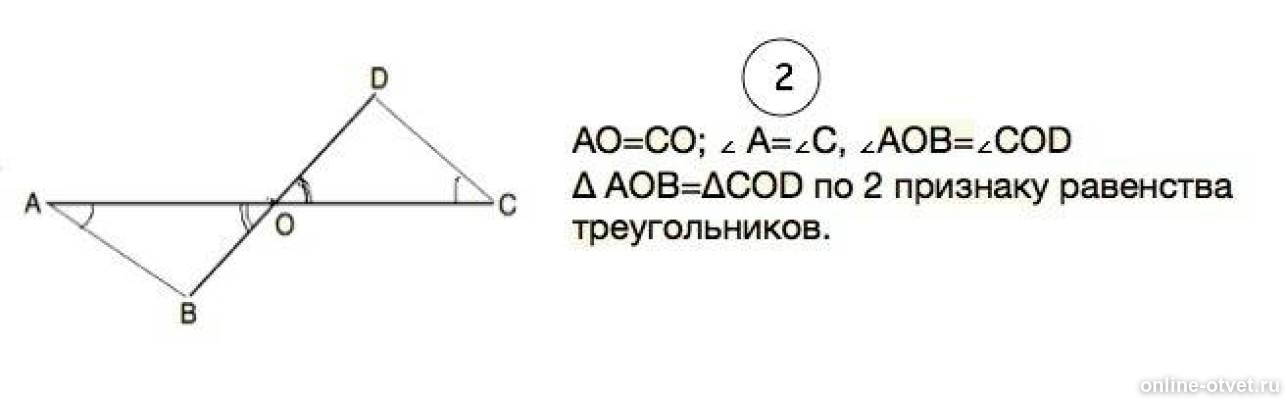
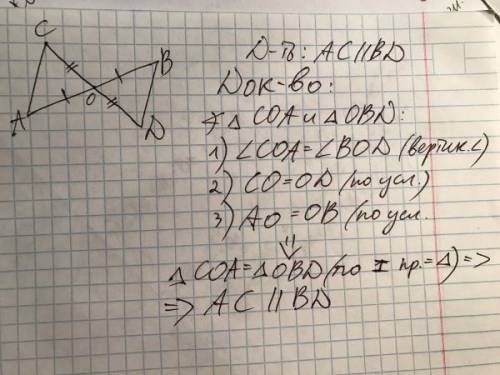
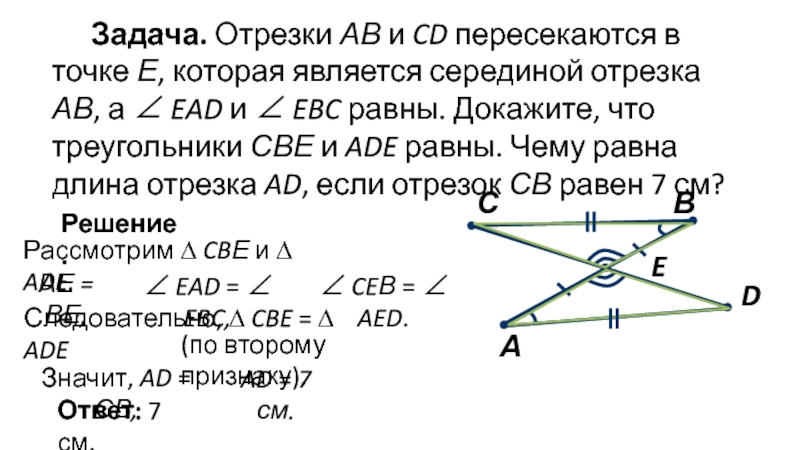
Определите все известные параметры треугольника, прежде чем использовать его свойства для решения задач.

Синус, косинус и тангенс Решение задач по геометрии

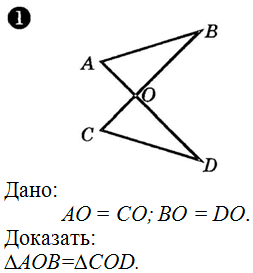
Используйте теорему о равенстве треугольников для доказательства их свойств и нахождения неизвестных сторон.

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия - Математика

При решении задач с треугольниками рисуйте схемы, чтобы наглядно видеть взаимосвязи между элементами.

№ 308 - Геометрия 7-9 класс Атанасян
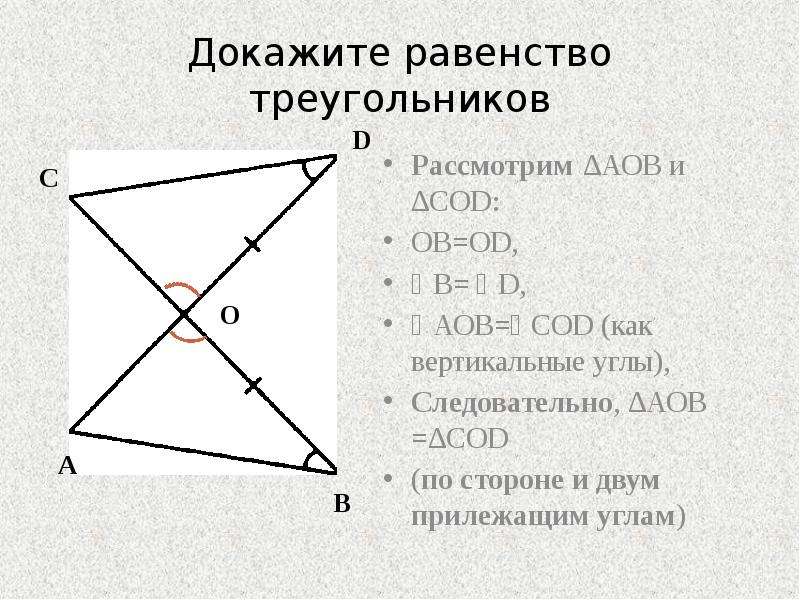
Проверяйте, являются ли треугольники равными по всем сторонам и углам, чтобы использовать их свойства корректно.

ТРИГОНОМЕТРИЯ - Синус, Косинус, Тангенс, Котангенс

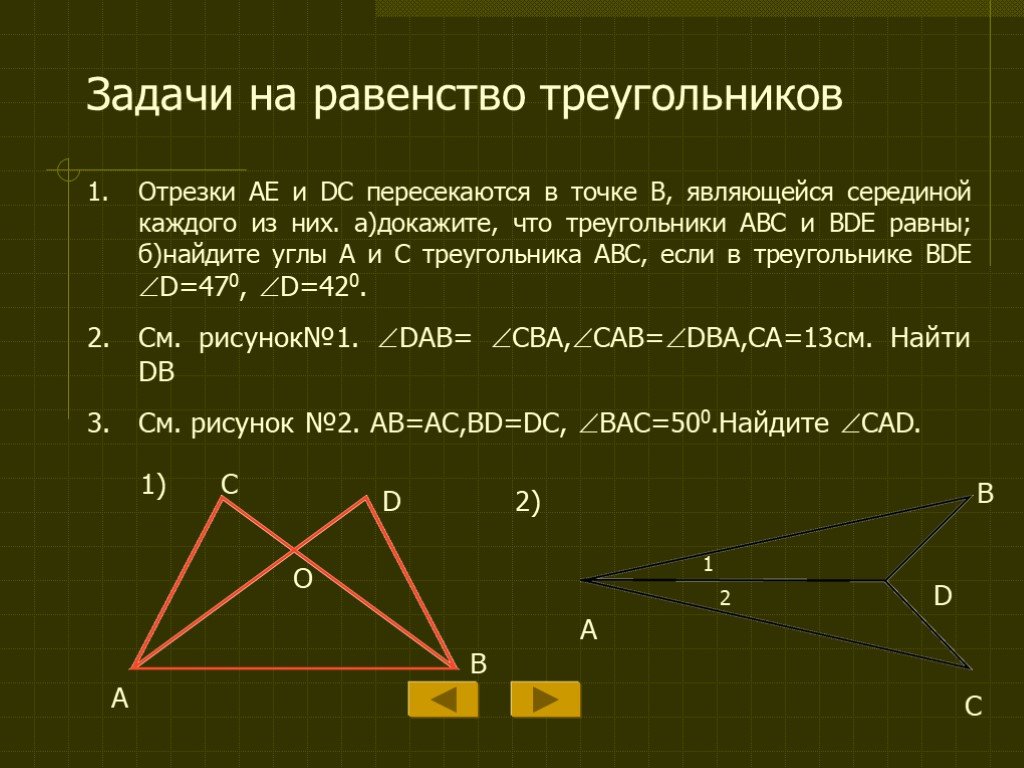
Знайте основные теоремы и определения, такие как теорема Пифагора и теорема о сумме углов треугольника.
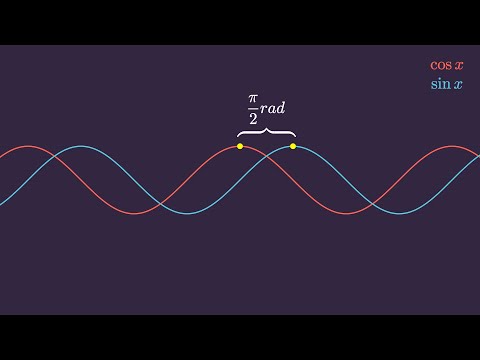
СУТЬ ТРИГОНОМЕТРИИ
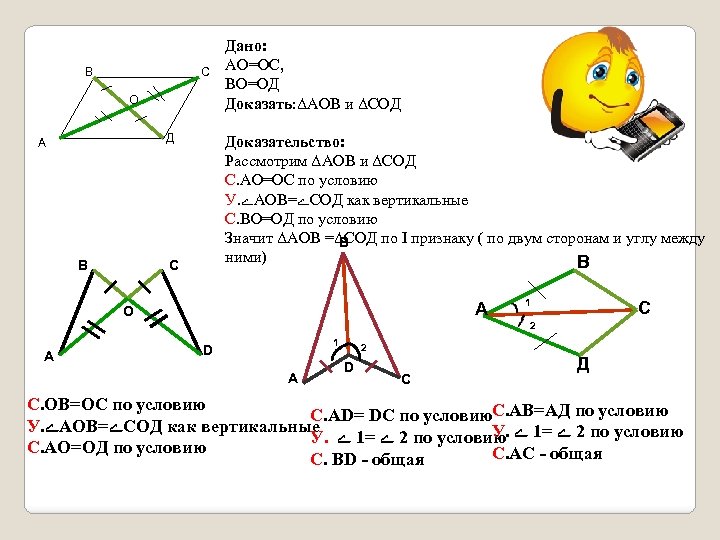
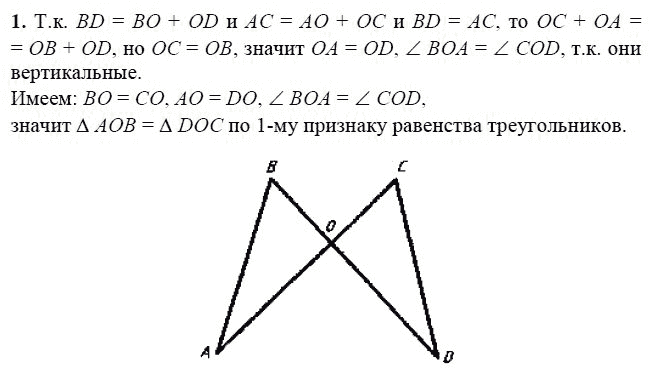
Внимательно относитесь к данным, особенно в задачах на равенство треугольников, чтобы избежать ошибок.
Используйте методы построения для проверки свойств треугольников и их равенства.

Подобие треугольников. Вся тема за 9 минут - ОГЭ по математике - Молодой Репетитор
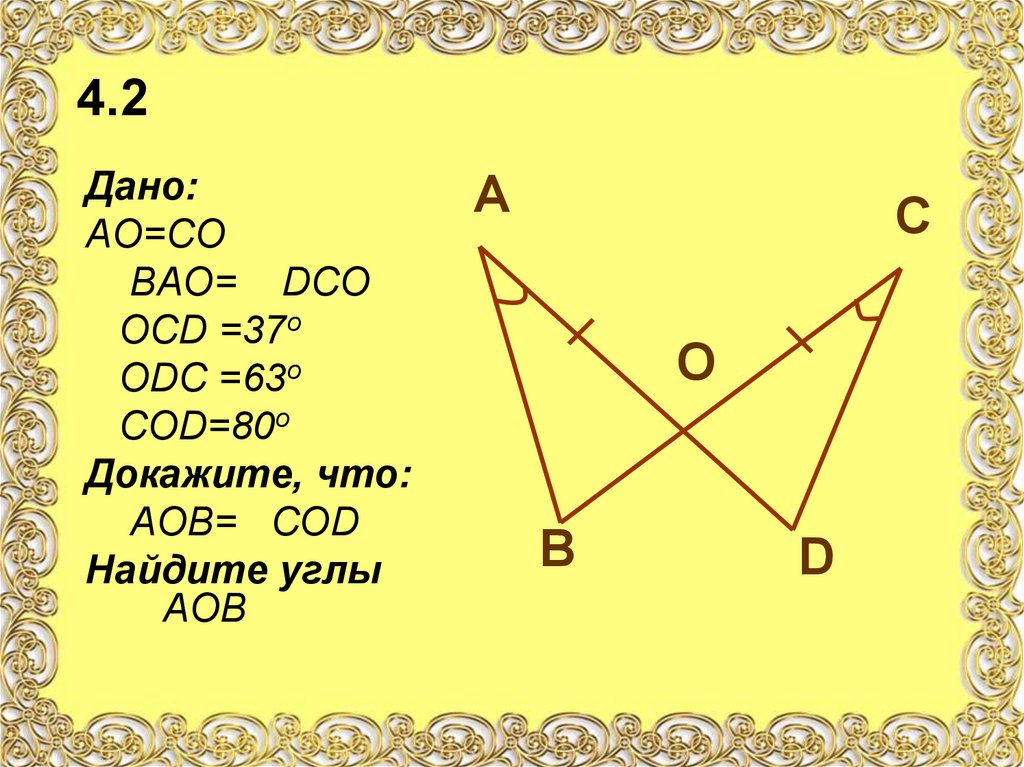

Рассматривайте треугольники в контексте более сложных фигур, чтобы лучше понимать их свойства.

Зачем нужны синусы и косинусы?
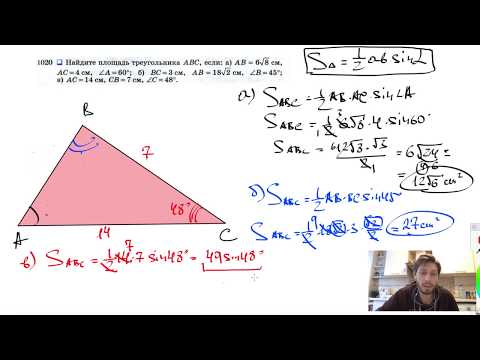
№1020. Найдите площадь треугольника ABC, если: а) АВ = = 6√8 см, АС=4 см, ∠А=60°;

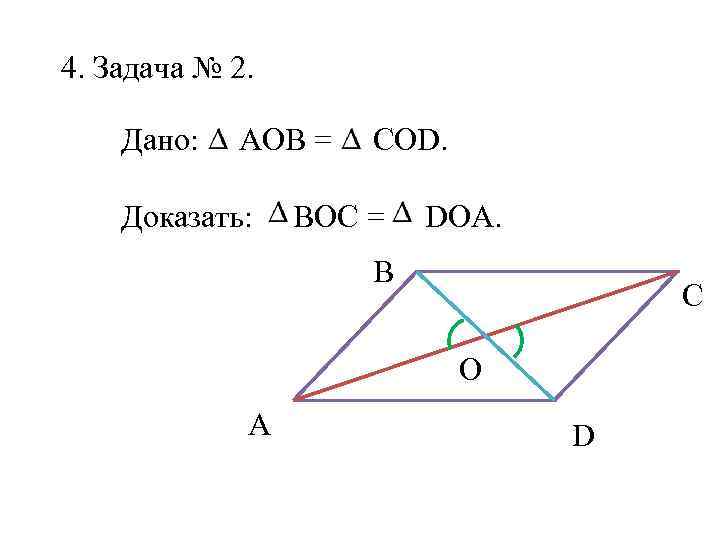
Практикуйтесь в решении различных типов задач на треугольники для улучшения своих навыков.

Задание №651 — Геометрия 8 класс (Атанасян)

Изучайте примеры решений и методические указания, чтобы расширить свои знания о свойствах треугольников.


Подобие треугольников. Признаки подобия треугольников (часть 1) - Математика