Простые методы для доказательства параллельности прямых а и б
В этой статье мы рассмотрим различные методы и полезные советы, которые помогут вам доказать параллельность прямых а и б, используя различные математические подходы.
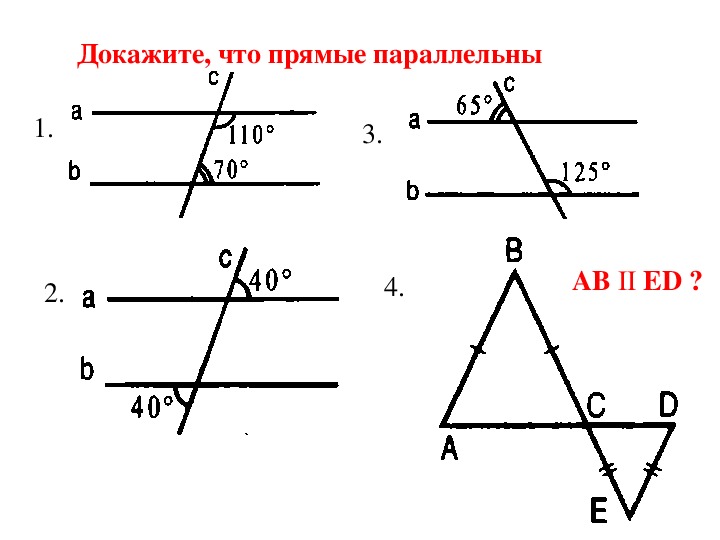
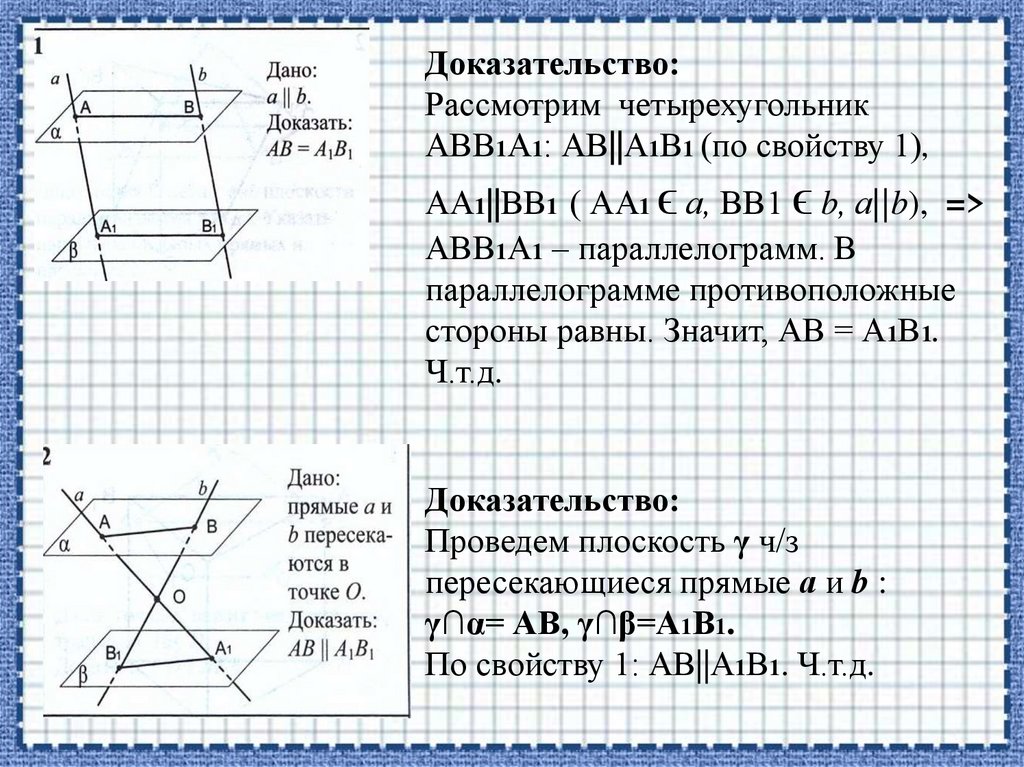
Используйте аксиому параллельности Евклида, которая гласит, что через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.

№385. Докажите теорему Фалеса: если на одной из двух прямых отложить последовательно
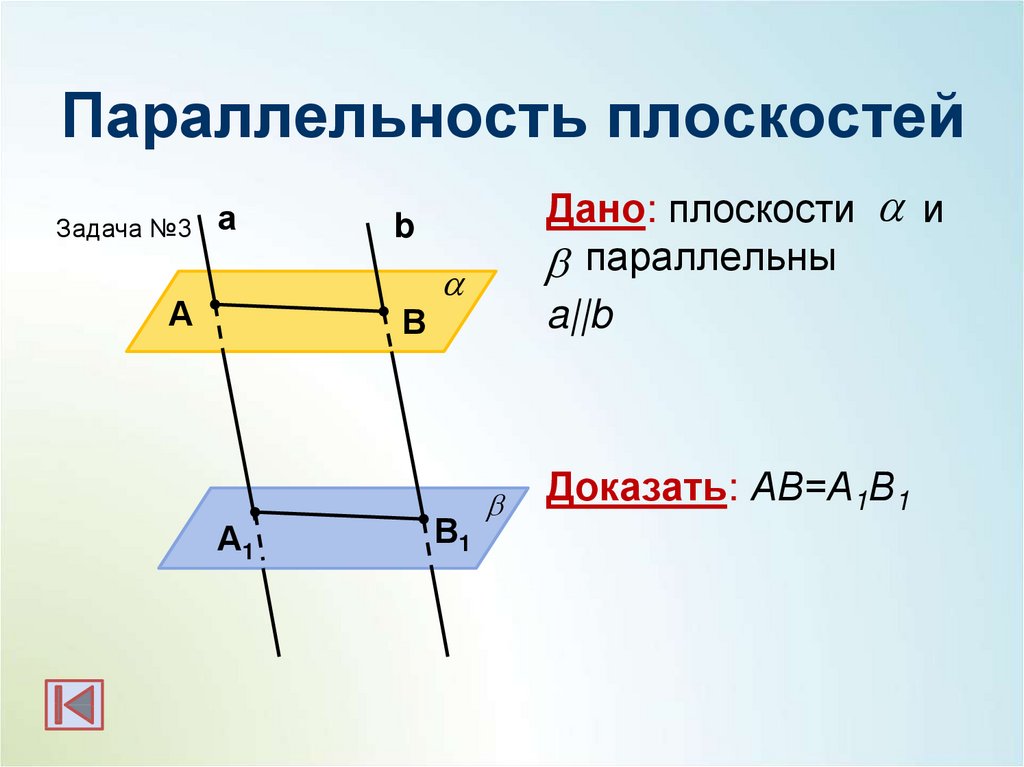
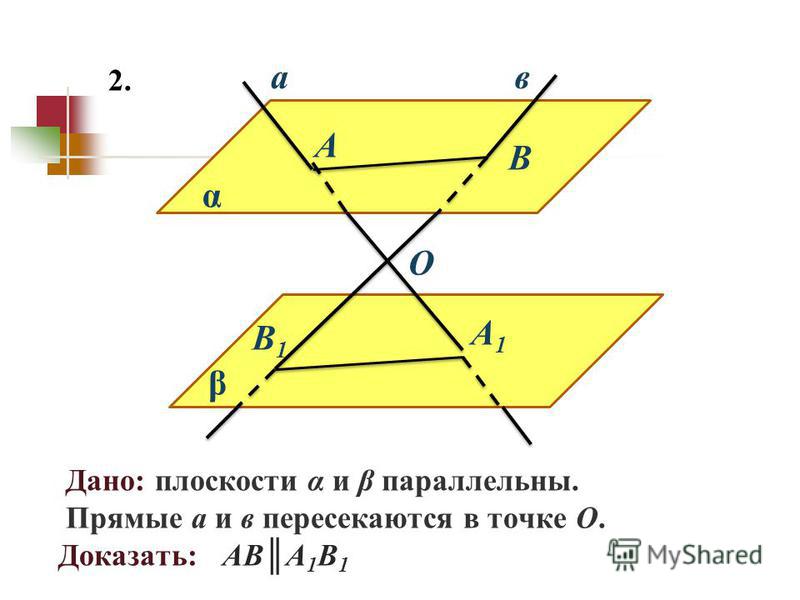
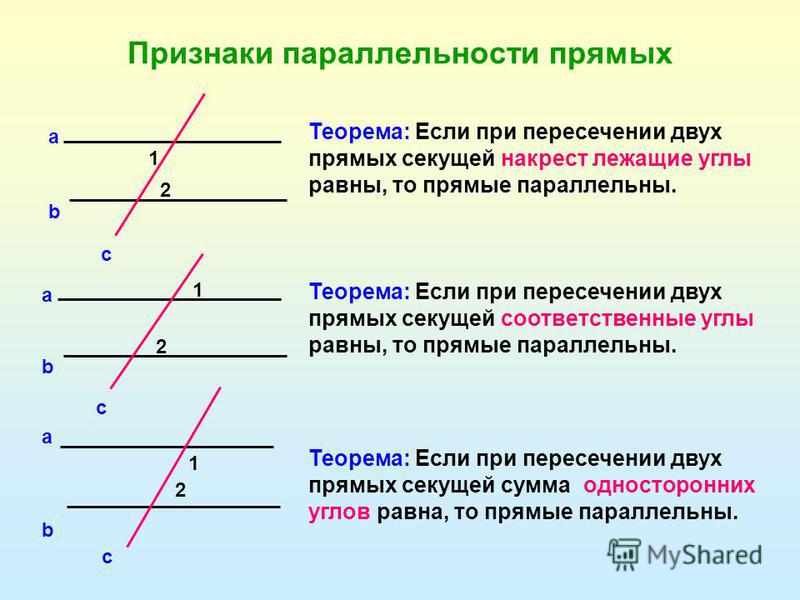
Примените теорему о параллельных прямых и накрест лежащих углах, которая утверждает, что если две прямые пересекаются третьей, и накрест лежащие углы равны, то эти прямые параллельны.

Теорема 14.3 Если соответственные углы равны, то прямые параллельны -- Геометрия 7 класс --
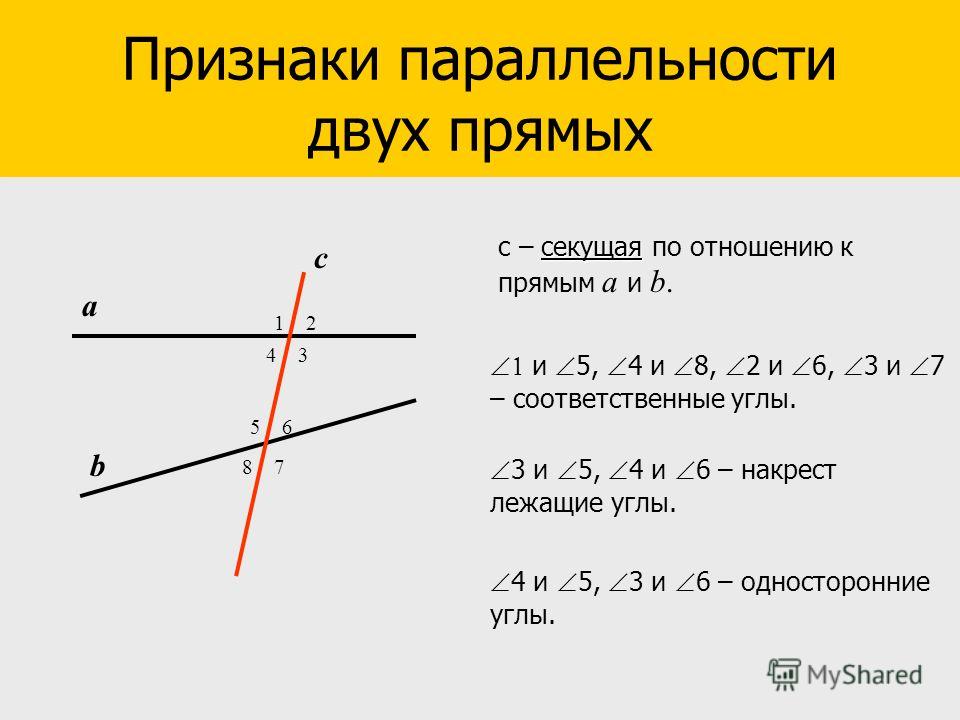
Используйте теорему о параллельных прямых и соответственных углах, которая утверждает, что если две прямые пересекаются третьей, и соответственные углы равны, то эти прямые параллельны.

Признаки параллельности прямых. Первый. Доказательство.
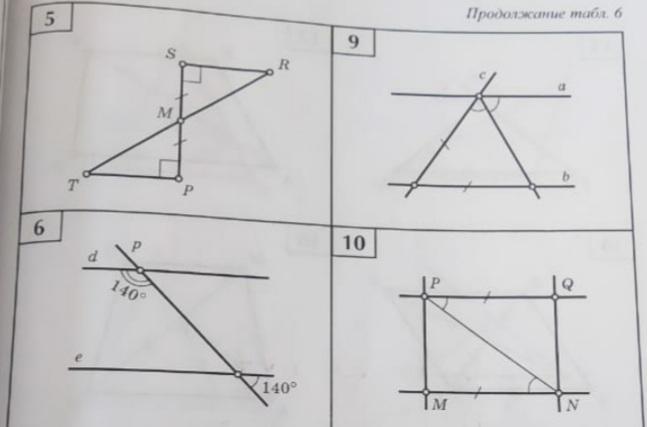
Примените теорему о параллельных прямых и односторонних углах, которая утверждает, что если две прямые пересекаются третьей, и сумма односторонних углов равна 180 градусам, то эти прямые параллельны.

Параллельные прямые - Математика - TutorOnline
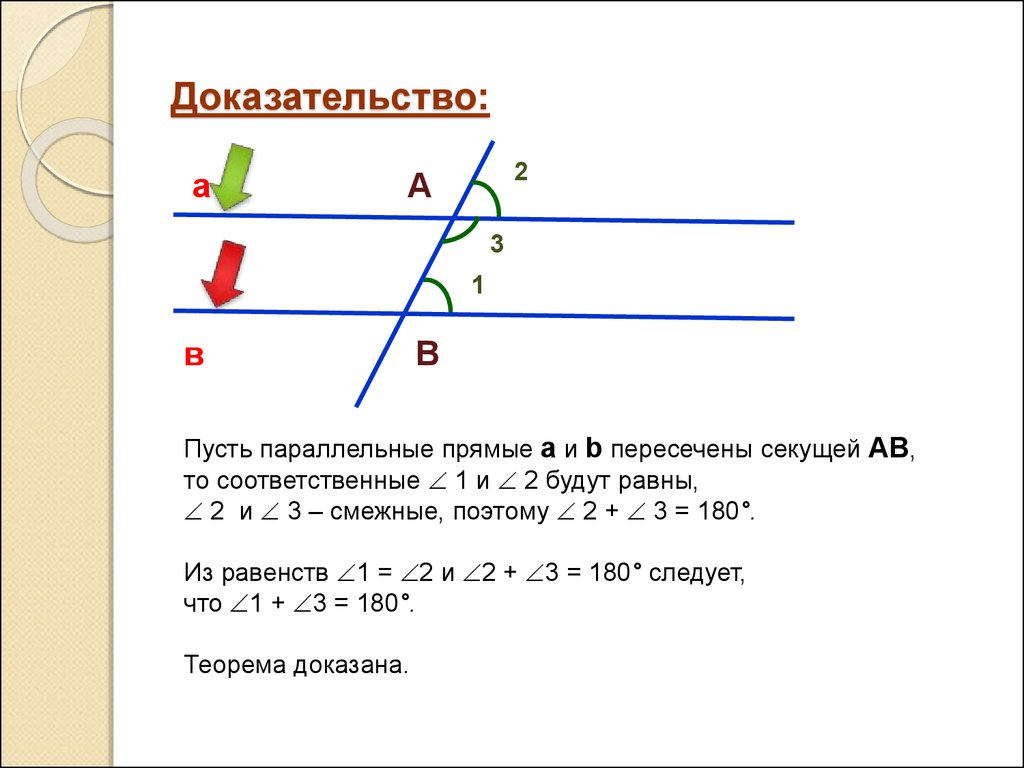

Используйте признак параллельности прямых по равенству внутренних углов при пересечении с секущей.

Теорема 14.1 Если накрест лежащие углы равны, то прямые параллельны
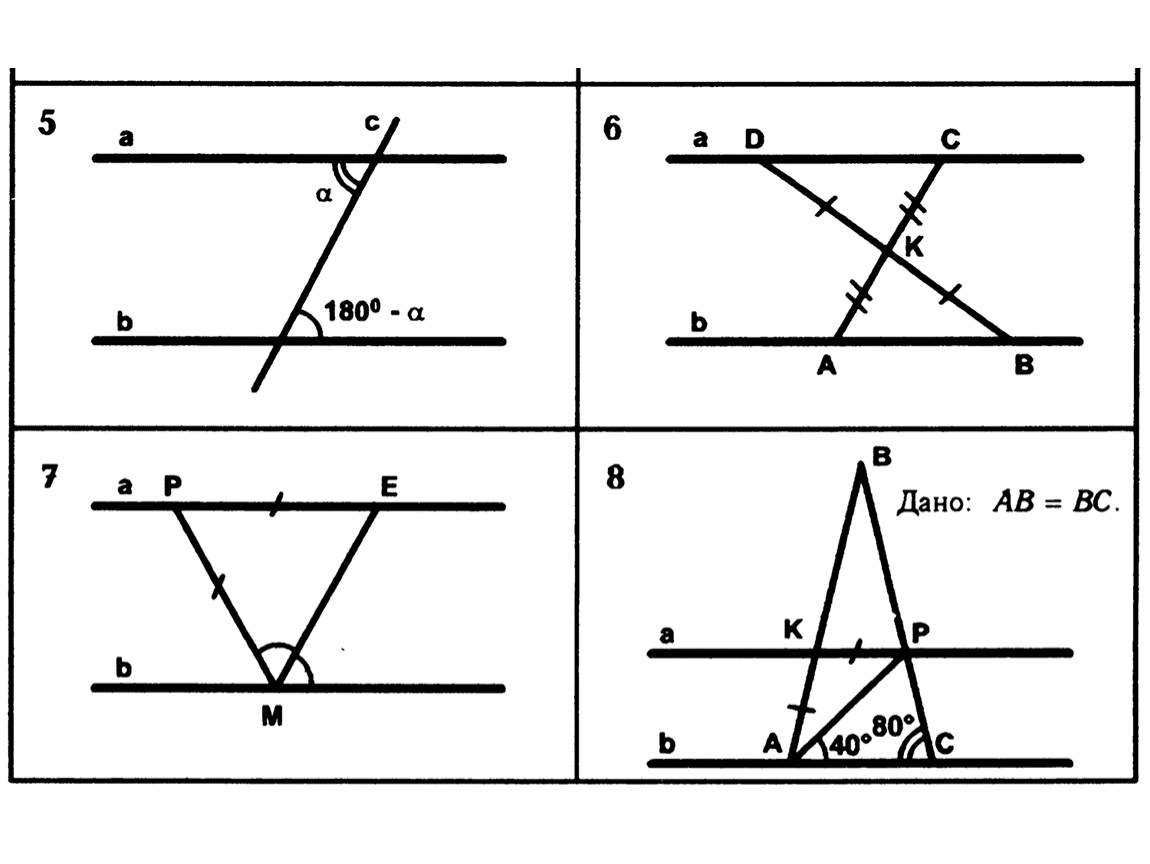
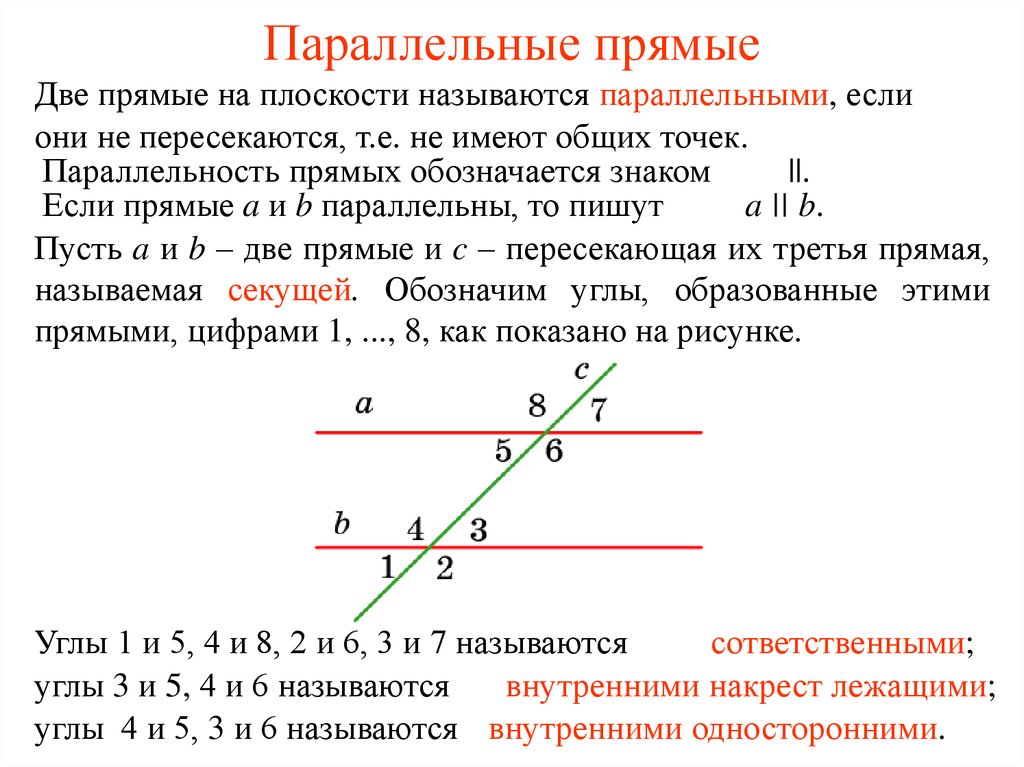
Примените метод координат: если прямые имеют одинаковый угловой коэффициент в уравнениях их линий, то они параллельны.
Используйте метод векторного произведения: если векторное произведение направляющих векторов двух прямых равно нулю, то эти прямые параллельны.
Примените свойства параллелограмма: если две пары противоположных сторон четырехугольника параллельны, то это параллелограмм.

7 класс, 25 урок, Признаки параллельности двух прямых


Используйте методы аналитической геометрии: сравните направления нормалей к прямым в их уравнениях.

Примените свойства трапеции: если основания трапеции параллельны, то это доказывает параллельность прямых.
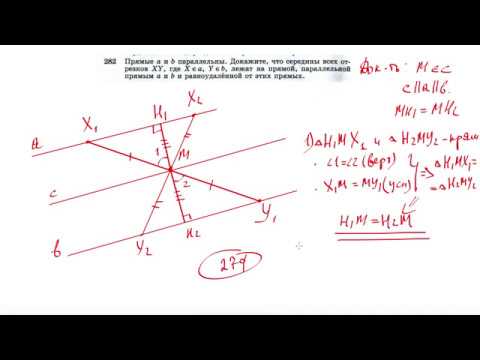
№282. Прямые а и b параллельны. Докажите, что середины всех отрезков XY, где Х∈а, Y∈b
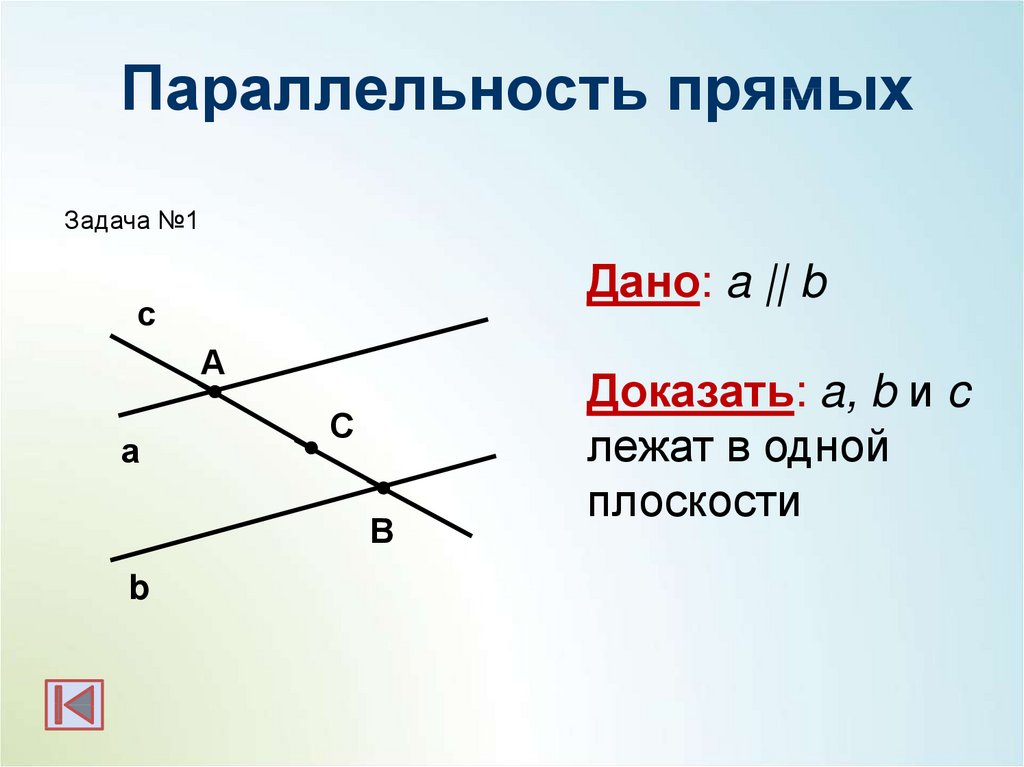

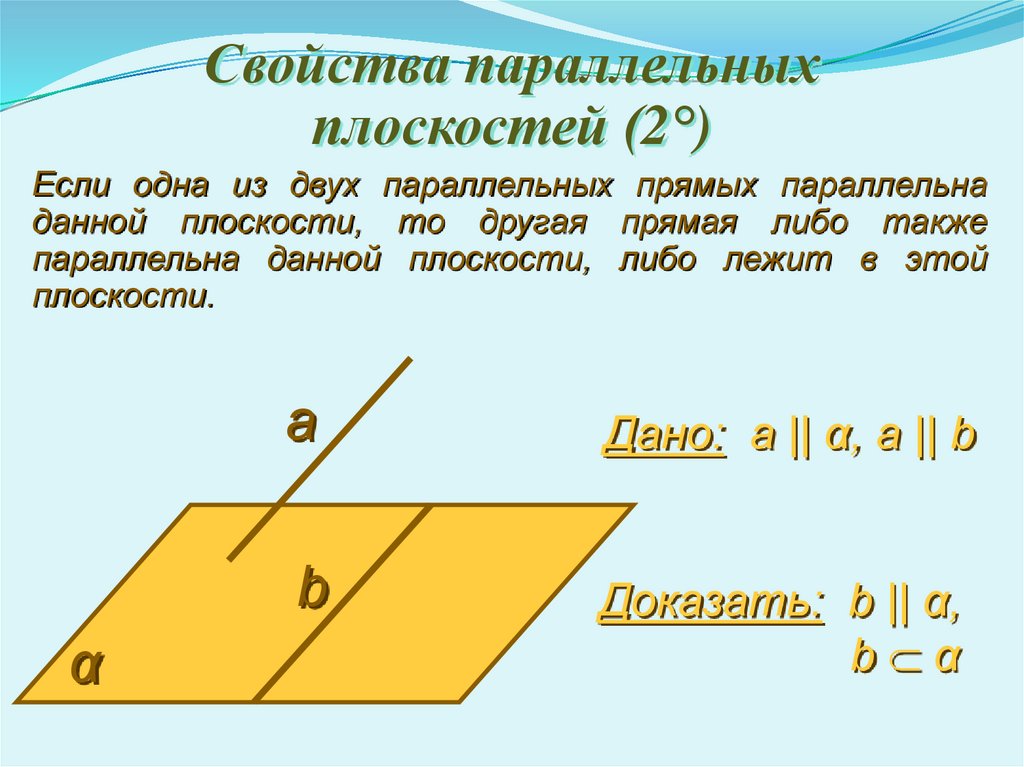
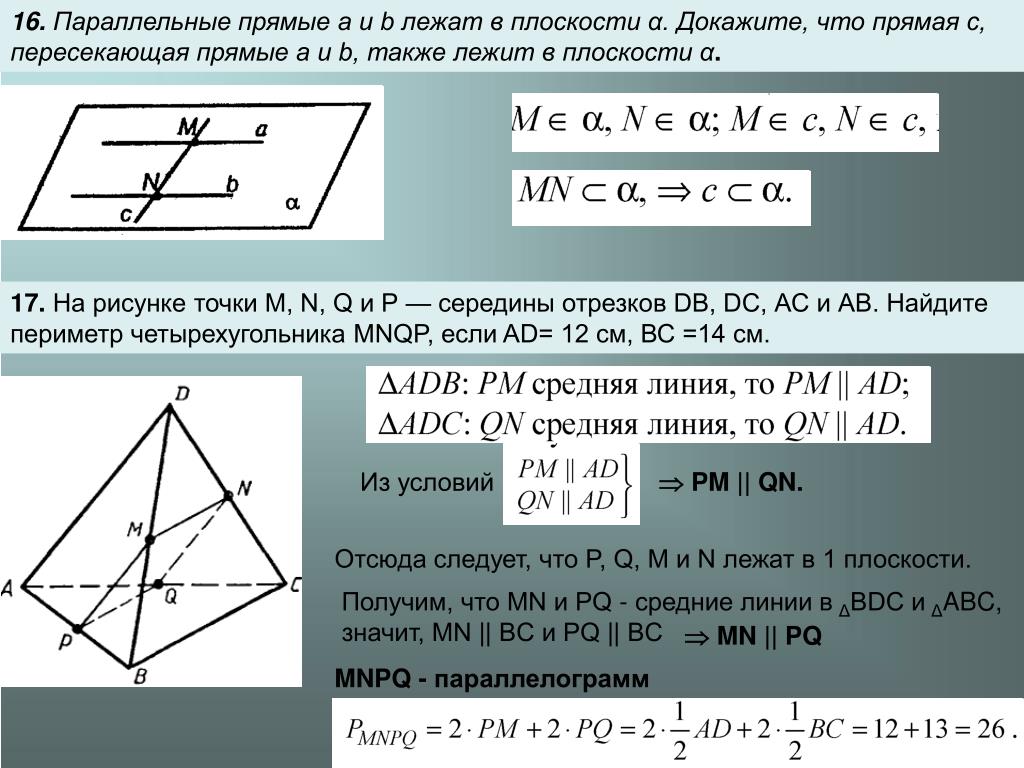
№16. Параллельные прямые a и b лежат в плоскости α. Докажите,