Геометрическое представление комплексных чисел: основные советы
В данной статье мы рассмотрим, как геометрически представить комплексные числа и какие полезные советы помогут вам лучше понять этот аспект математики. Геометрическое представление позволяет визуализировать комплексные числа в виде точек на комплексной плоскости, что упрощает их анализ и применение.


Начните с основ: комплексное число можно представить в виде точки на комплексной плоскости, где действительная часть является координатой по оси X, а мнимая — по оси Y.

Комплексные числа. Тригонометрическая форма. Формула Муавра - Ботай со мной #040 - Борис Трушин !

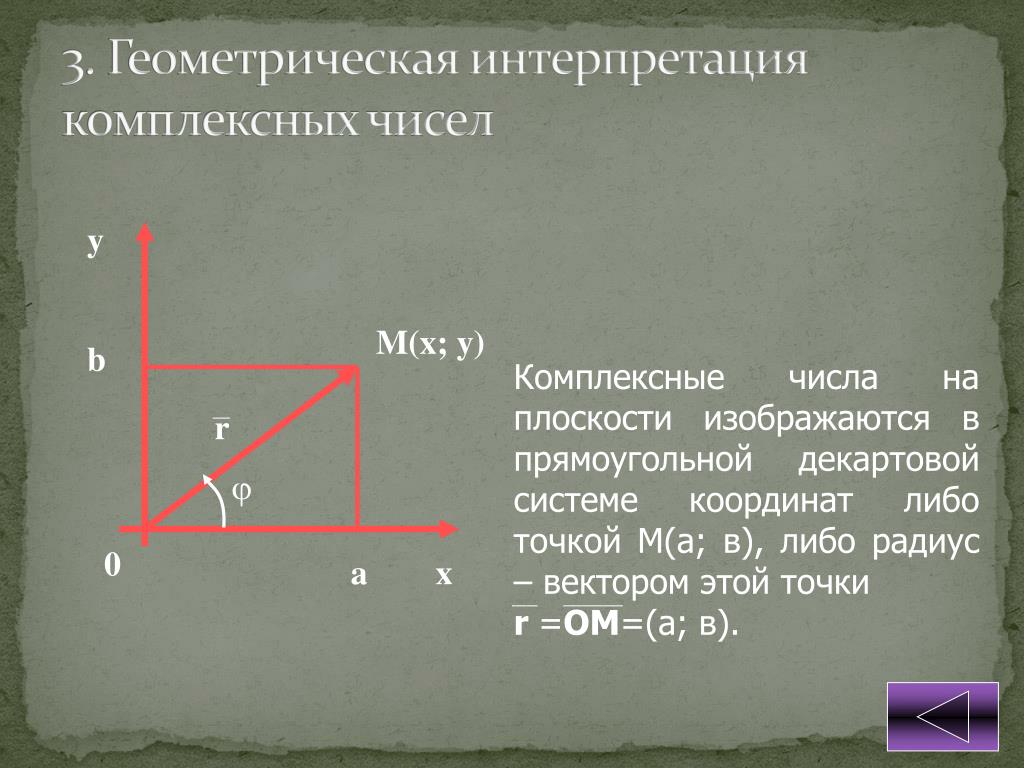
Используйте полярные координаты для более удобного представления комплексных чисел, что позволит вам работать с их модулем и аргументом.

ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА ЗАПИСИ КОМПЛЕКСНОГО ЧИСЛА

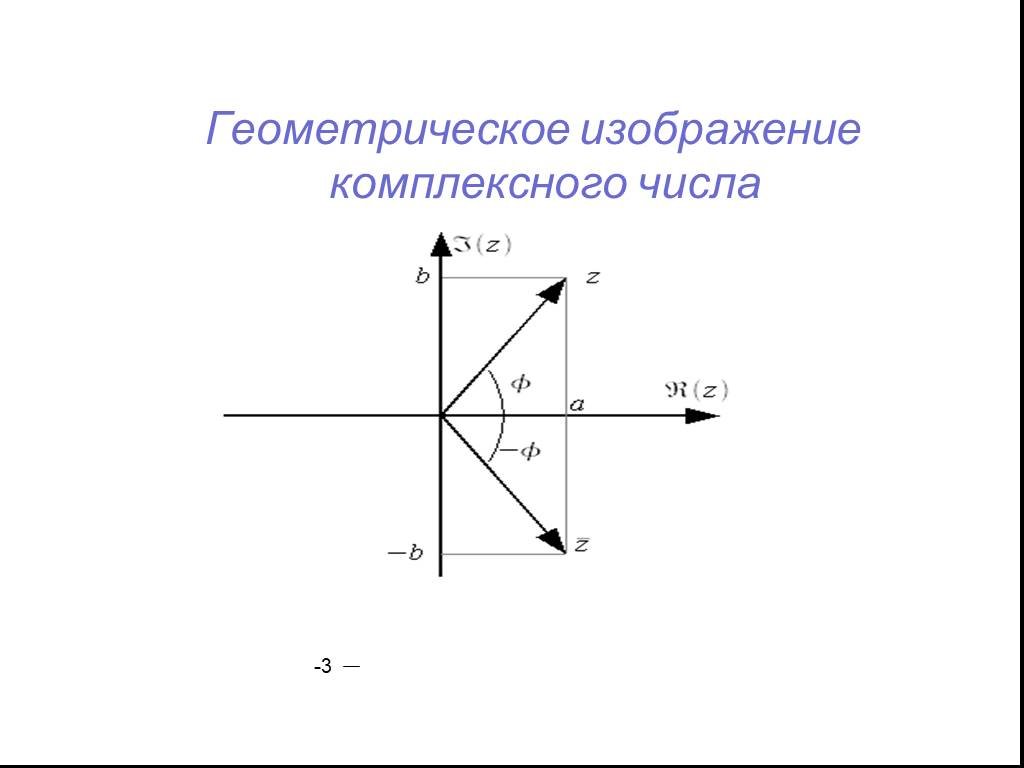
Запомните, что модуль комплексного числа равен расстоянию от начала координат до точки, а аргумент — угол между положительной осью X и линией, соединяющей начало координат с точкой.
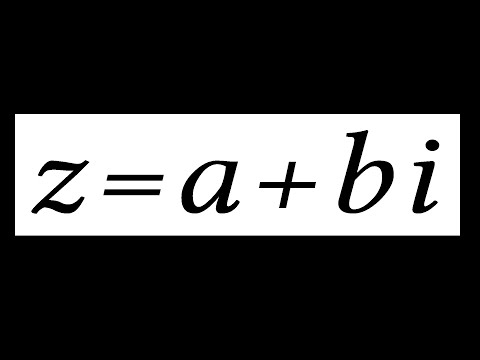
КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТ


При выполнении операций над комплексными числами, таких как сложение и умножение, учтите их геометрическое представление для упрощения расчетов.

Математика без Ху%!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.

Для преобразования комплексных чисел между алгебраической и геометрической формами используйте формулы для нахождения модуля и аргумента числа.

4. Показательная форма комплексного числа

Используйте графические программы или калькуляторы для визуализации комплексных чисел и их операций, это поможет лучше понять их свойства.
Практикуйтесь в построении графиков комплексных чисел, чтобы лучше освоить их представление и операции на комплексной плоскости.

1.8 Комплексные числа


Понимание геометрического представления поможет при решении задач, связанных с преобразованиями и анализом комплексных чисел.

10 класс, 34 урок, Тригонометрическая форма записи комплексного числа
Используйте таблицы значений модулей и аргументов для упрощения вычислений и проверки результатов.


Регулярно возвращайтесь к основам и проверяйте свое понимание, чтобы уверенно использовать геометрическое представление комплексных чисел в различных задачах.

Тригонометрическая форма комплексного числа