Интересные факты и советы по тетраэдру и октаэдру
В этом разделе мы рассмотрим геометрические формы тетраэдра и октаэдра, их свойства, применения и интересные факты. Эти формы широко используются в различных областях науки и искусства, и их изучение может быть полезным и увлекательным.
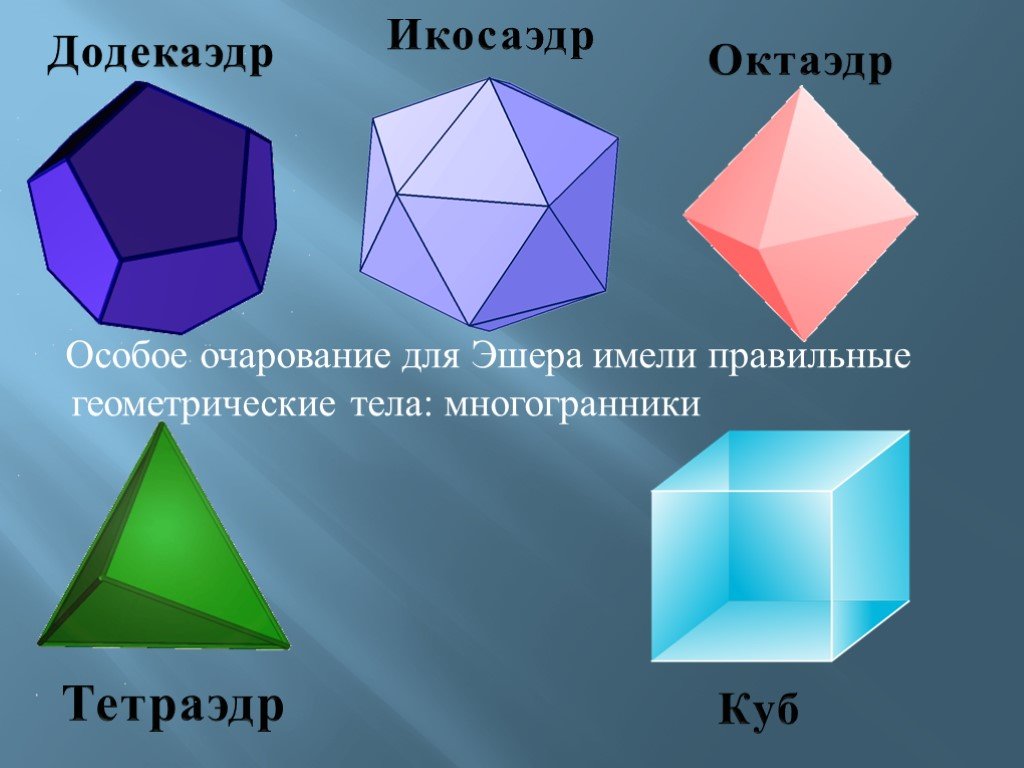

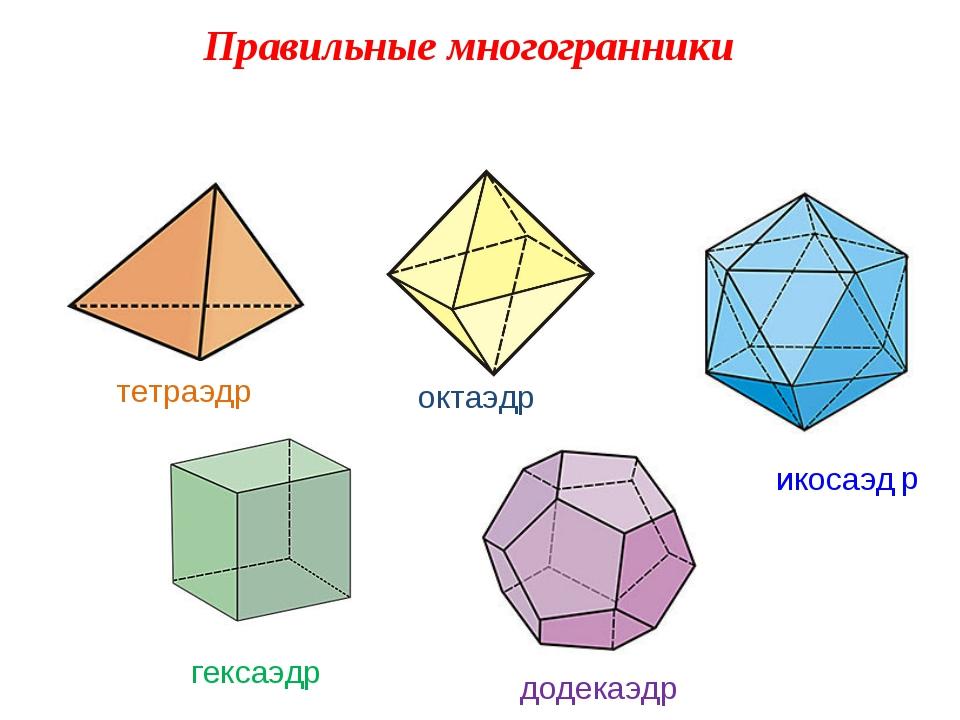
При изучении тетраэдра и октаэдра полезно создать модели из бумаги или картона, чтобы лучше понять их геометрическую структуру.

КАК СДЕЛАТЬ ЗВЁЗДЧАТЫЙ ОКТАЭДР? ЗВЁЗДЧАТЫЙ ОКТАЭДР. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ИЗ БУМАГИ. - #RAIDOTV

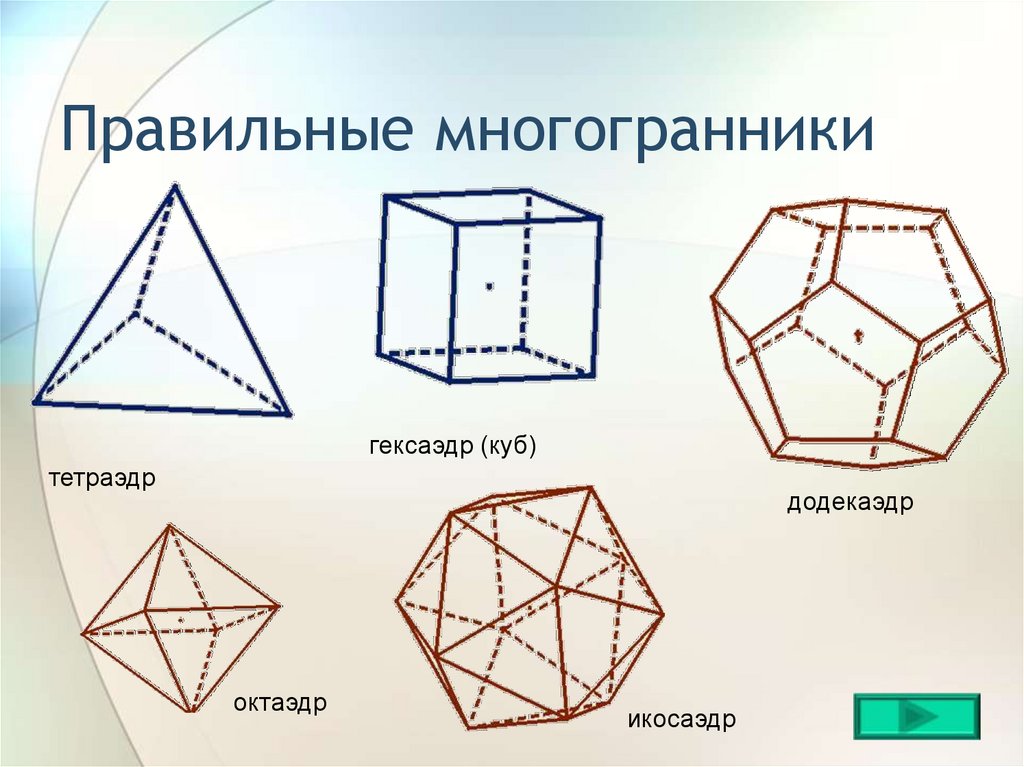
Попробуйте нарисовать проекции этих форм на плоскости для лучшего понимания их трехмерных свойств.

Икосаэдр из бумаги. Чертёж развертки икосаэдра.

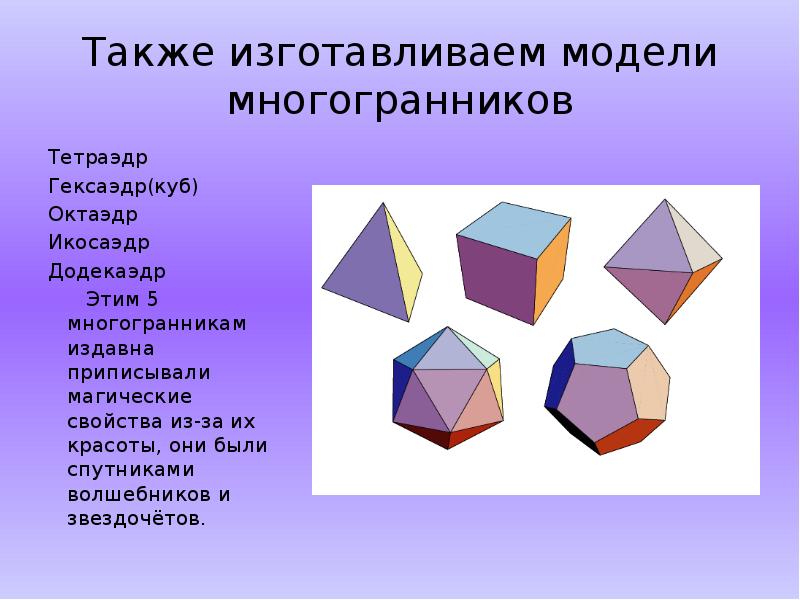
Изучите, как тетраэдры и октаэдры используются в архитектуре и дизайне для создания прочных и эстетически привлекательных структур.

Развертка октаэдра - это легко! Как сделать октаэдр из бумаги?

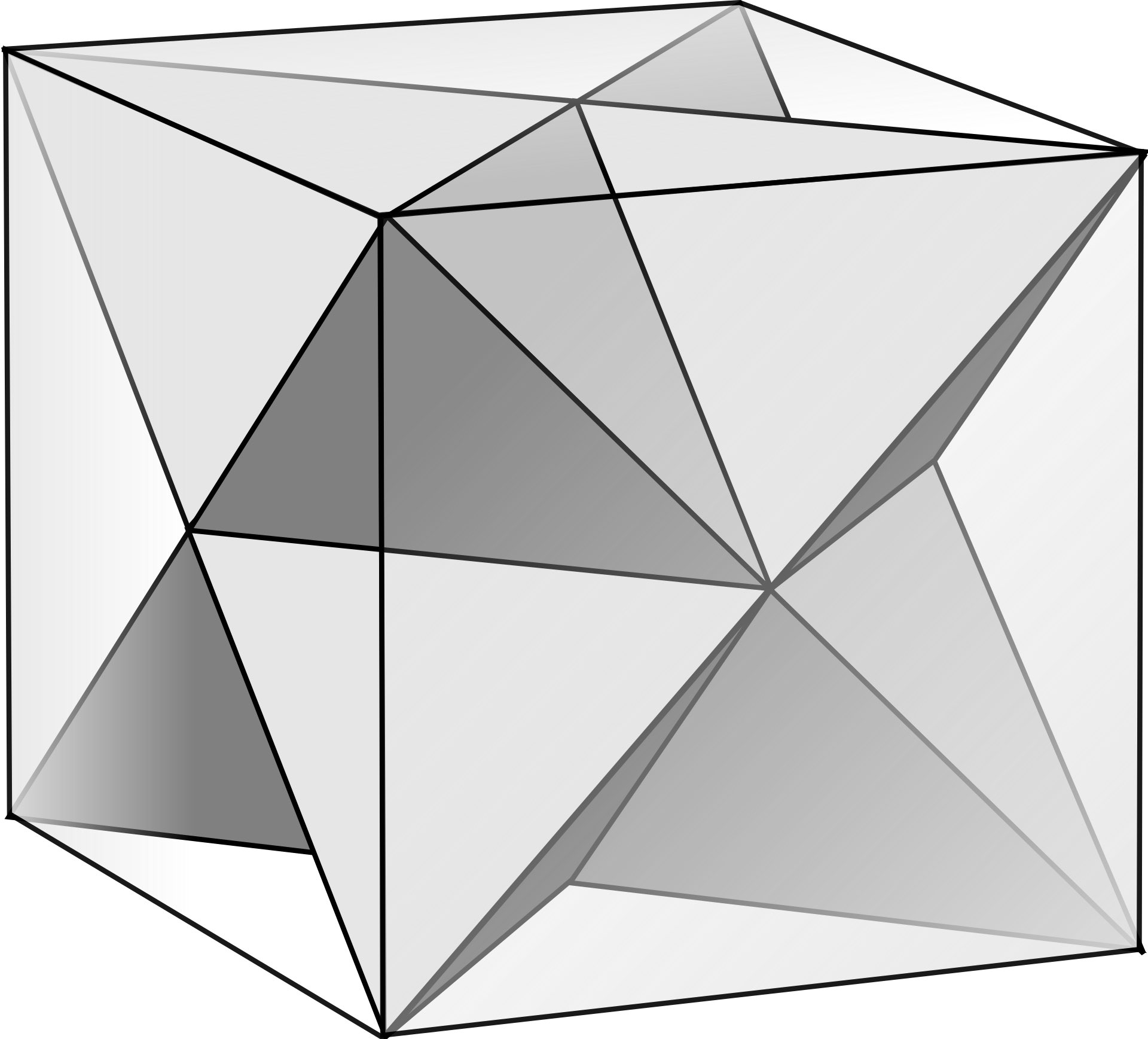
Используйте геометрические программы для моделирования тетраэдра и октаэдра, чтобы визуализировать их свойства и взаимосвязи.
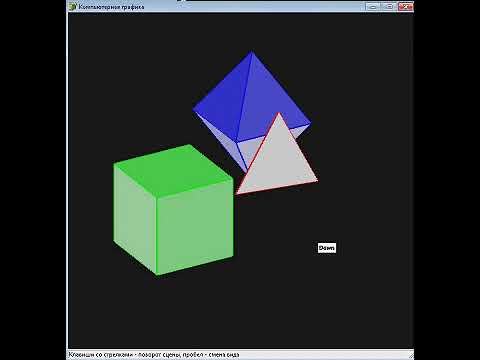
Построение изометрической аксонометрической проекции трехмерных фигур (тетраэдр, гексаэдр и октаэдр)

Сравните свойства тетраэдра и октаэдра с другими геометрическими формами, чтобы лучше понять их уникальные характеристики.

Гороховый конструктор: октаэдр и икосаэдр. 3D конструктор своими руками. Геометрия для детей

Читайте научные статьи и книги о многогранниках для углубленного изучения тетраэдра и октаэдра.
Изучите, как тетраэдры и октаэдры могут быть использованы в компьютерной графике и анимации.

тетраэдр и октаэдр из металла
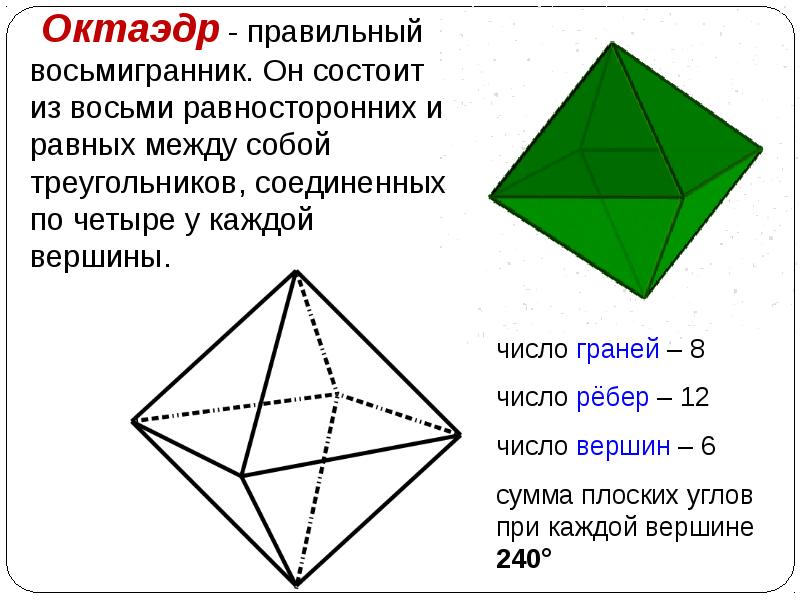
Попробуйте использовать тетраэдр и октаэдр для создания абстрактных произведений искусства.

Тетраэдр. 10 класс.

Платоновы тела: Тетраэдр, Куб, Октаэдр, Икосаэдр, Додекаэдр
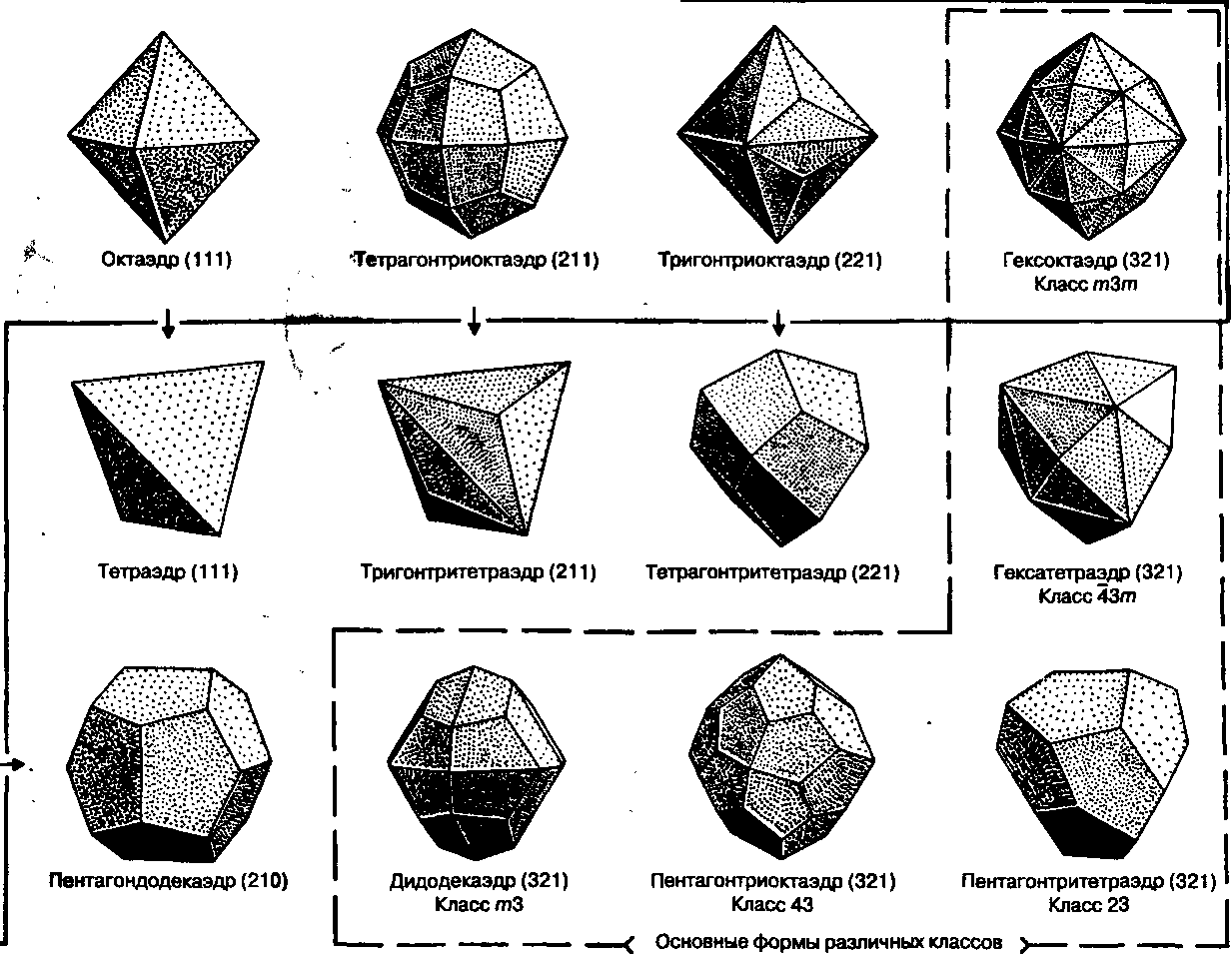
Посетите выставки или музейные экспозиции, где представлены модели многогранников, чтобы увидеть их в реальной жизни.

Как сделать Тетраэдр - Платоново тело - Многогранник


Исследуйте роль тетраэдра и октаэдра в кристаллографии и других научных областях для более глубокого понимания их применения.

Многогранники : Тетраэдр, Октаэдр, Икосаэдр, Гексаэдр, Додека