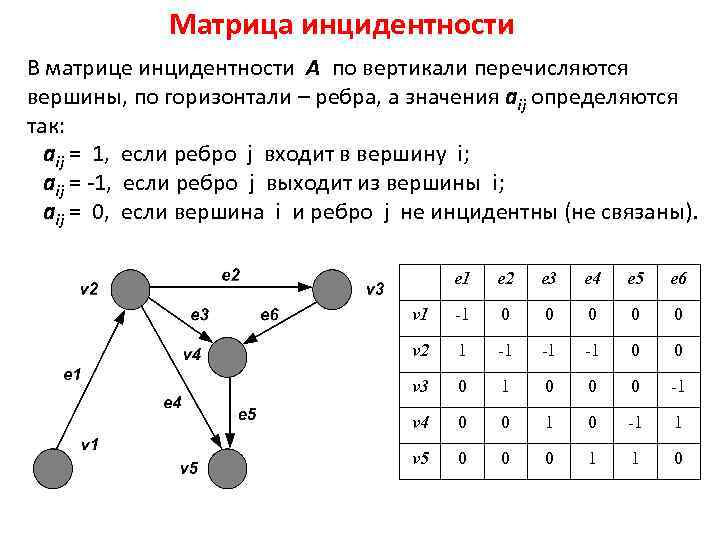
Введение в матричное представление графов и их свойства
В этом разделе вы узнаете о методах представления графов с использованием матриц, включая смежности и инцидентности, а также их применения в различных задачах и алгоритмах.

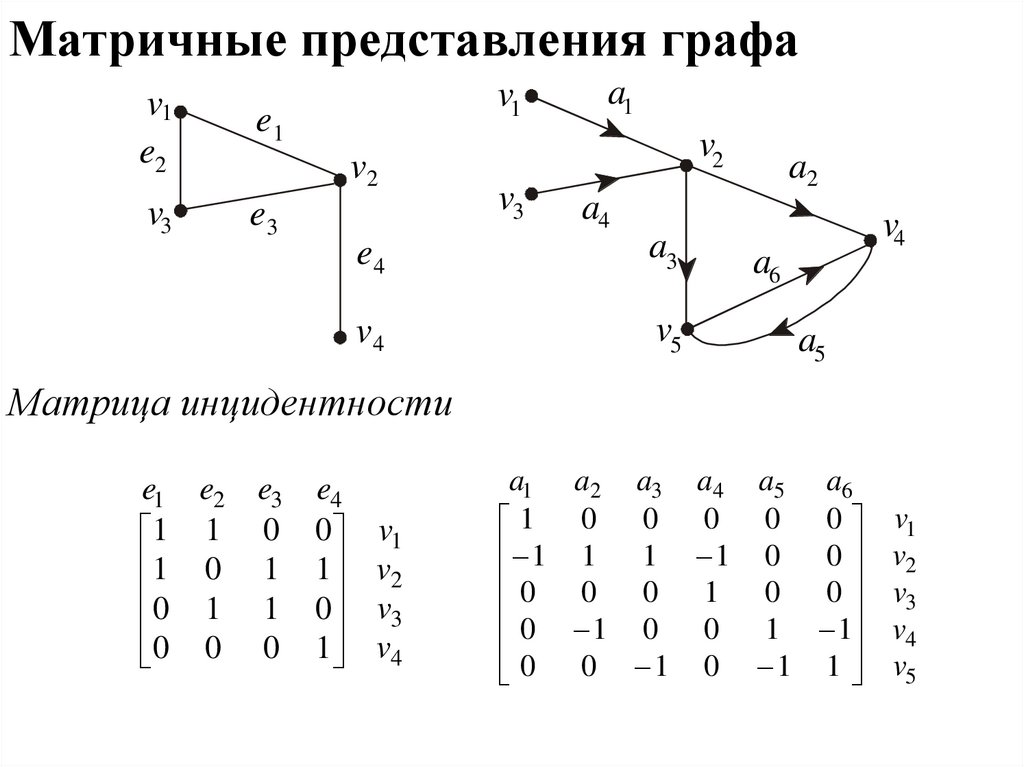
Используйте матрицу смежности для эффективного представления связей между вершинами в графе.
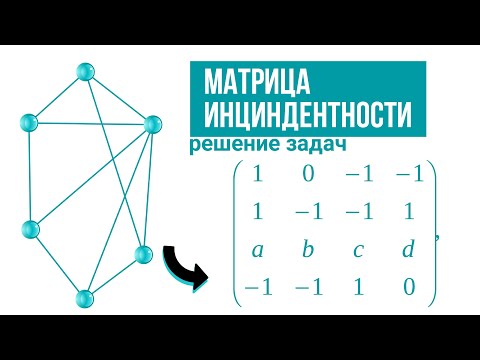
Как найти матрицу инцидентности
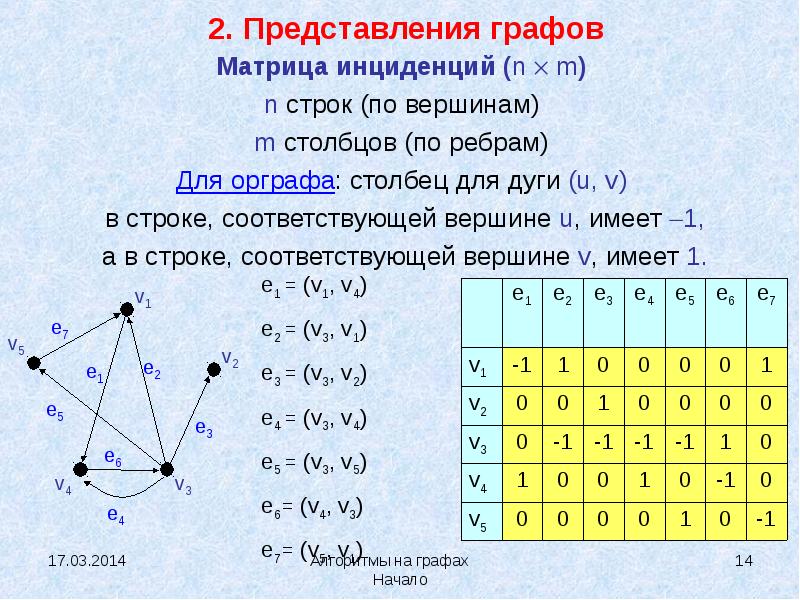

Для направленных графов учитывайте матрицу смежности с направленными ребрами, чтобы корректно отобразить направление связи.

Информатика. Теория графов. Хранение графа: матрица смежности. Центр онлайн-обучения «Фоксфорд»

Используйте матрицу инцидентности для графов, где важно учитывать связь между вершинами и рёбрами.

Способы представления графов: список рёбер, матрица смежности, списки смежности
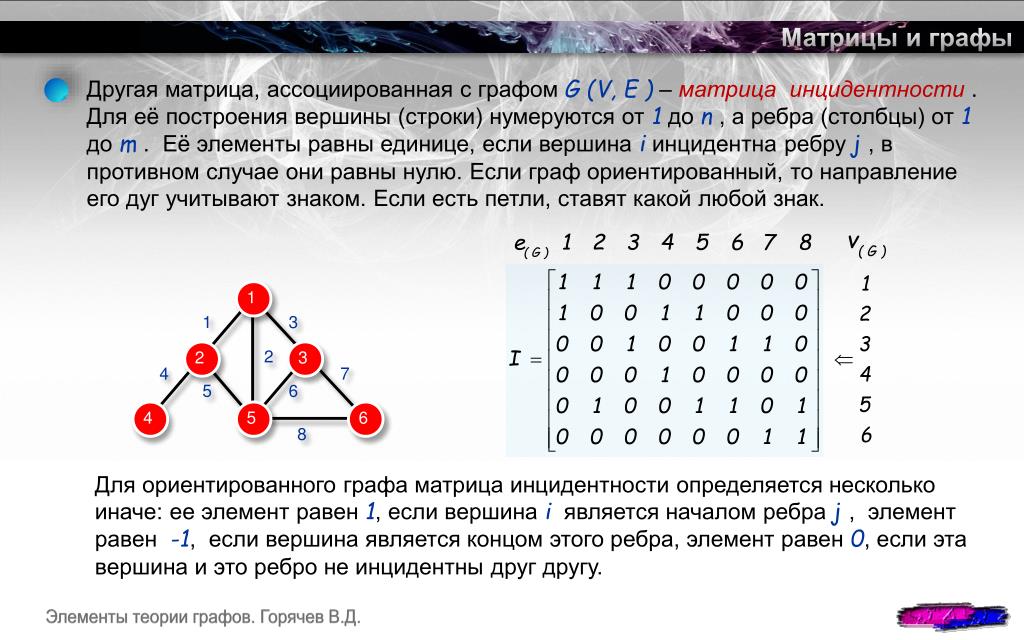
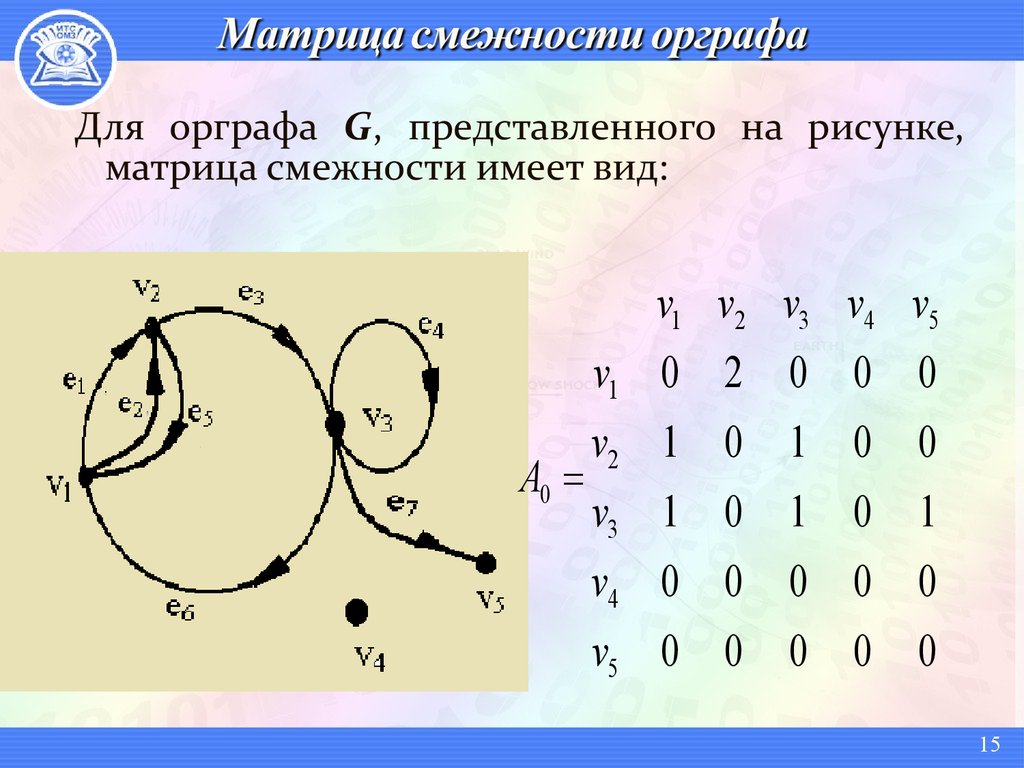
Не забывайте, что для больших графов использование матриц может потребовать значительных вычислительных ресурсов.
Способы задать граф. Матрица векторов смежности

При работе с разреженными графами рассматривайте использование специализированных структур данных для экономии памяти.
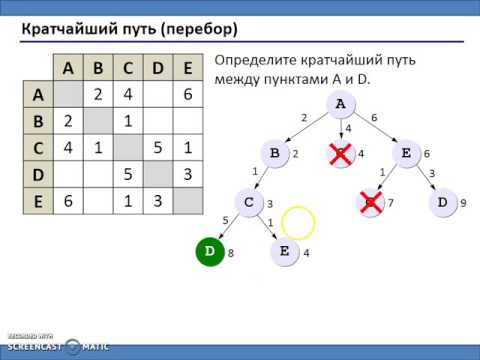
Графы
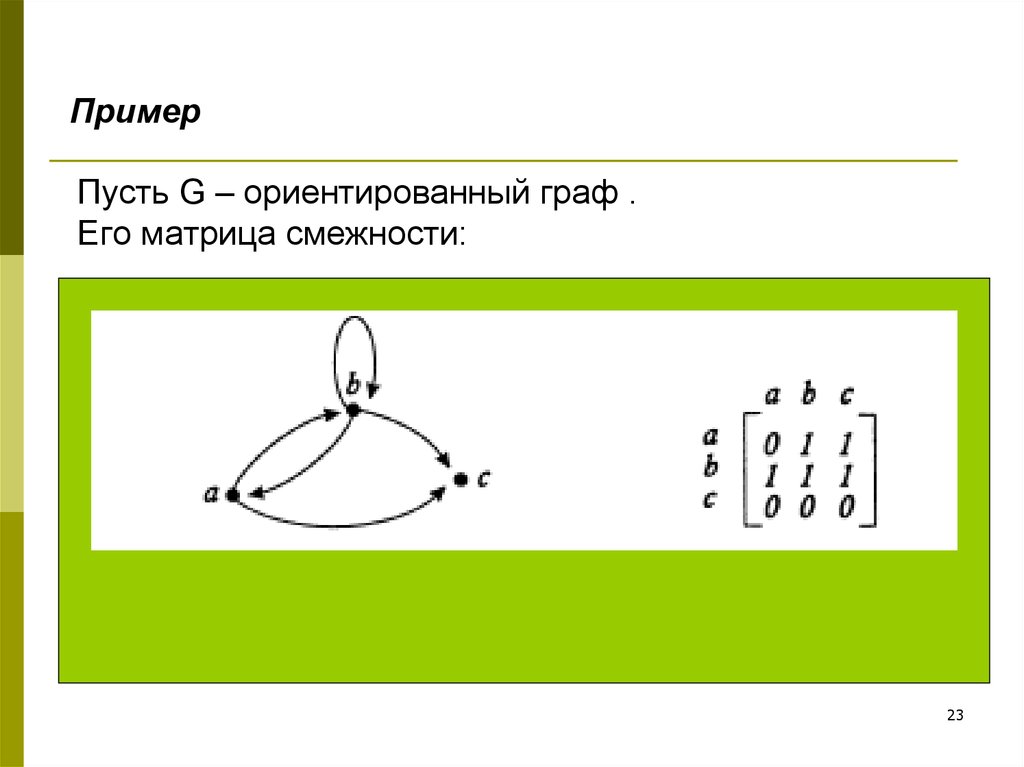
При реализации алгоритмов на графах, таких как поиск в глубину или в ширину, учитывайте специфику матрицы смежности для оптимизации.

Диаметр графа. Радиус. Эксцентриситет. Центр

Экспериментируйте с различными типами матриц (например, бинарные, вещественные) в зависимости от задачи, которую вы решаете.
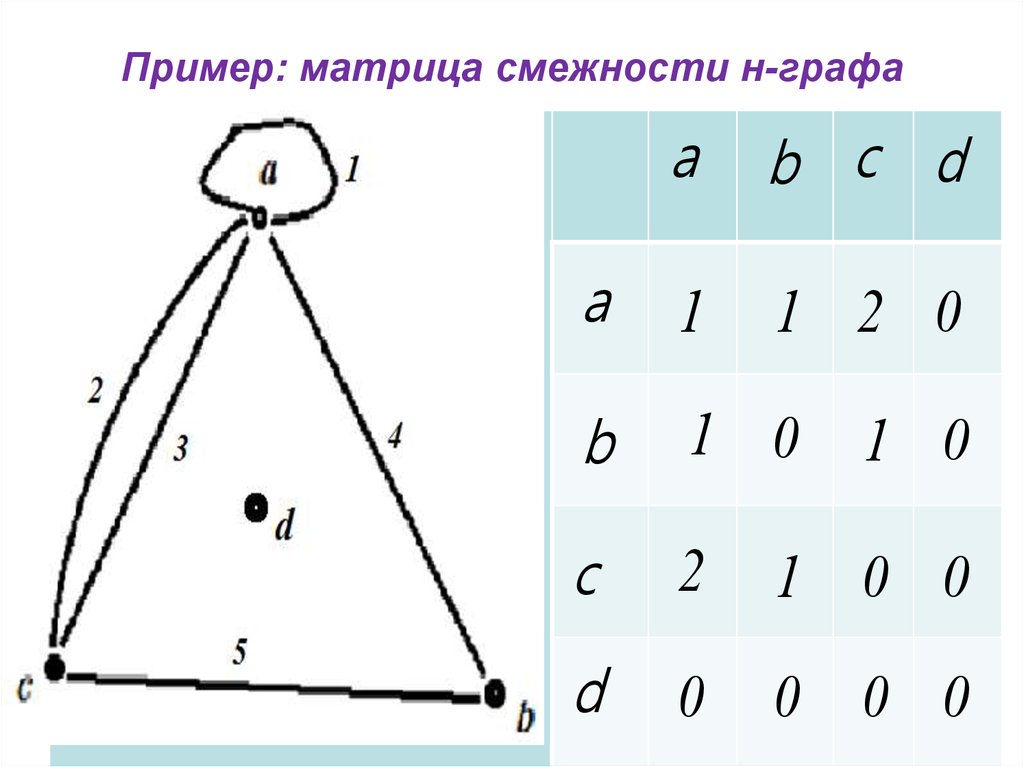
Используйте библиотеки и инструменты, которые поддерживают эффективные операции над матрицами для работы с графами.
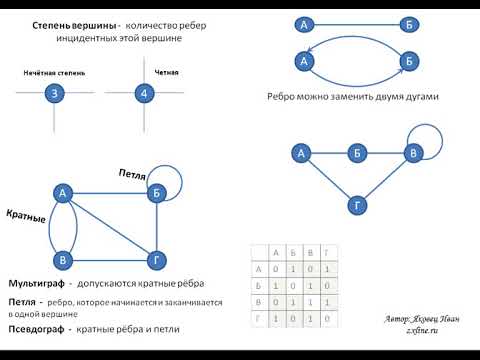
Графы, вершины, ребра, инцидентность, смежность
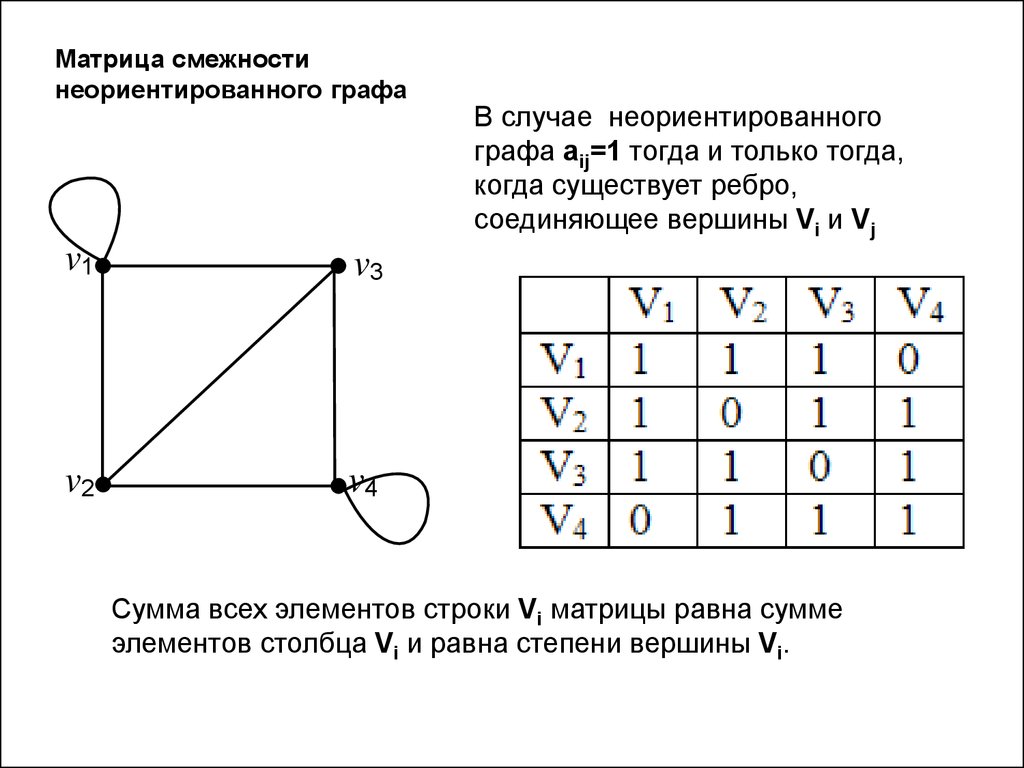
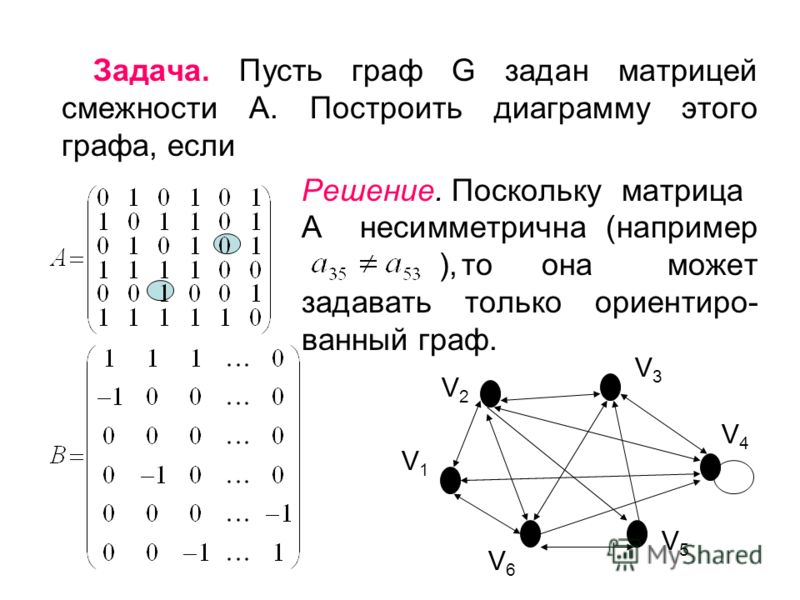
Обратите внимание на изменения в матрице при добавлении или удалении рёбер, чтобы поддерживать актуальность представления графа.
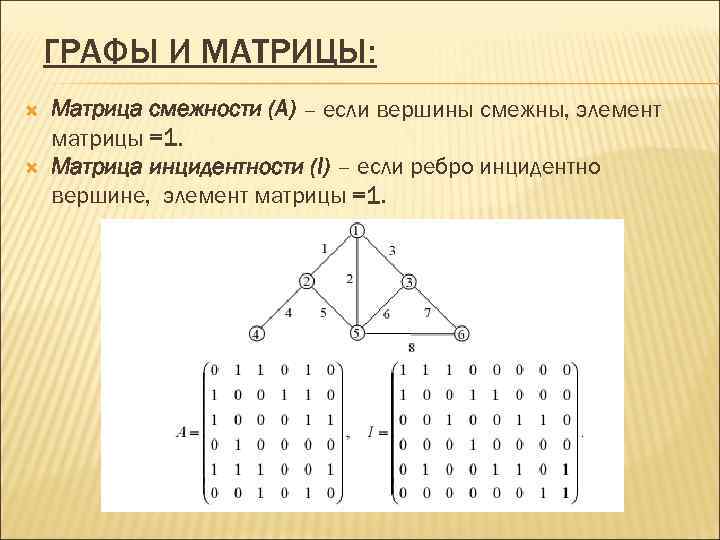
Учтите, что матричное представление графа может быть полезно для решения задач оптимизации и анализа свойств графов.

Матрицы графа и их связь