Советы по анализу графиков дифференцируемых функций для студентов
В этой статье мы рассмотрим, как правильно интерпретировать графики дифференцируемых функций, что поможет лучше понять их поведение и особенности. Подборка фотографий и полезных советов облегчит изучение этой темы.

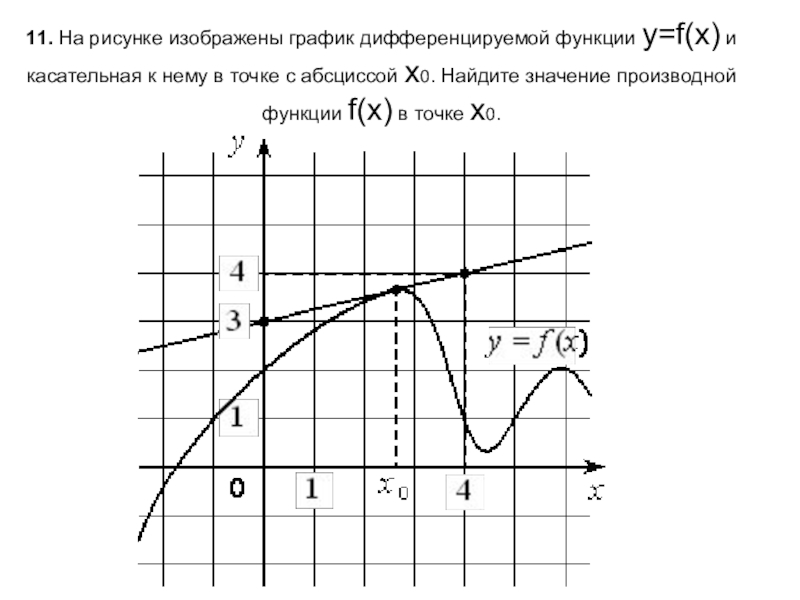
Обратите внимание на точки, где график функции имеет вертикальные касательные: такие точки могут указывать на особенности функции, такие как экстремумы.
На рисунке изображён график —производной функции определённой на интервале . В какой точке отрезка
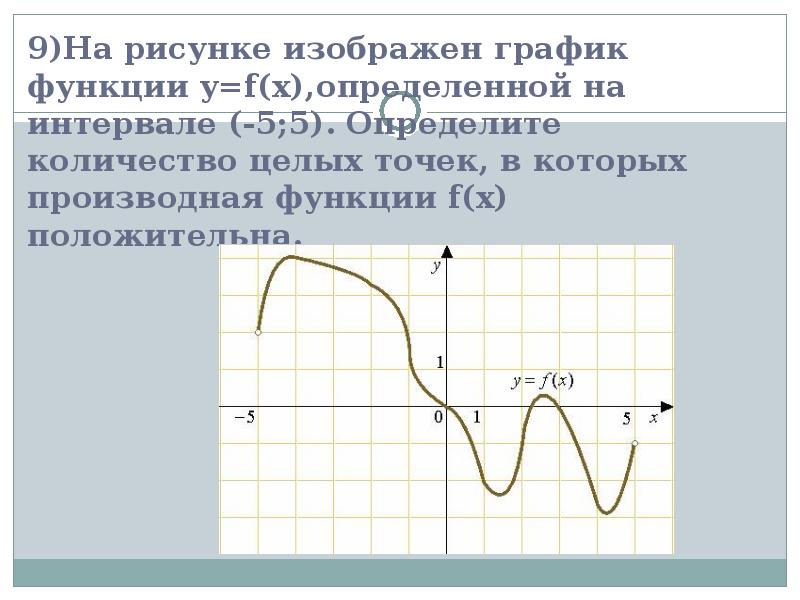
Изучите поведение функции на промежутках между критическими точками, чтобы понять, как меняется её наклон и кривизна.
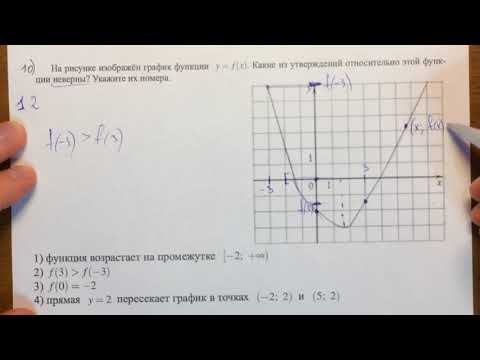
ОГЭ математика Алгебра #13.18 Задача 10🔴
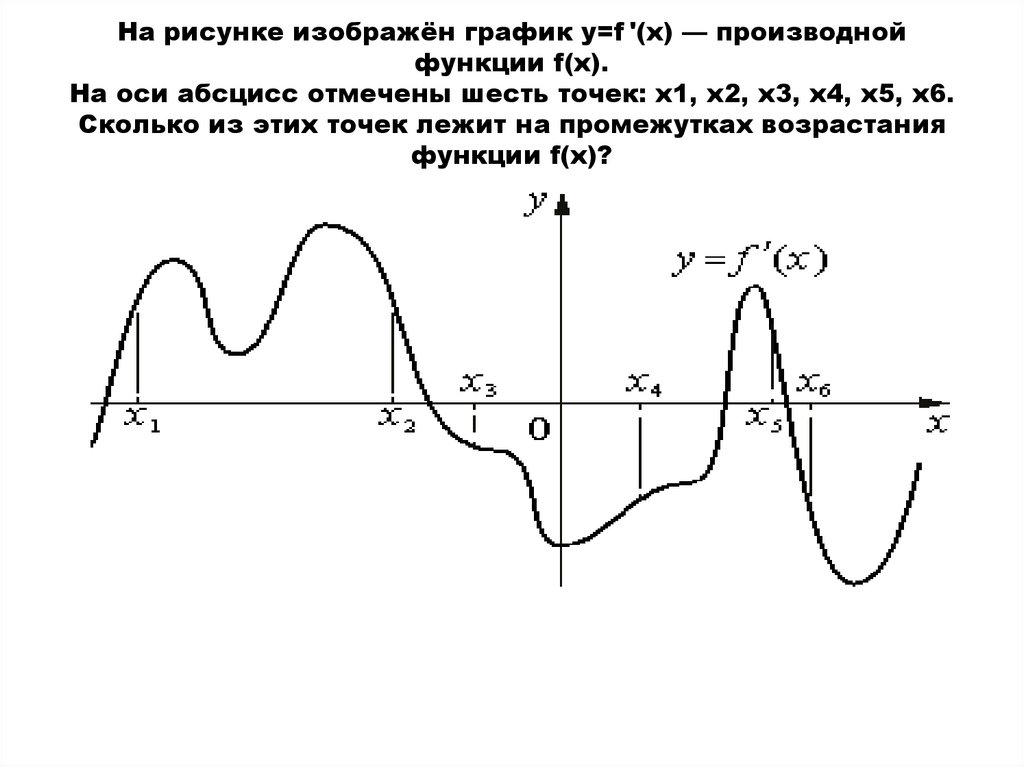
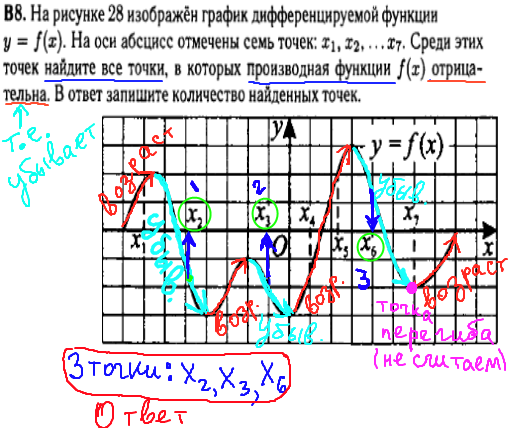
Используйте производную функции для нахождения точек перегиба графика и определения его выпуклости или вогнутости.
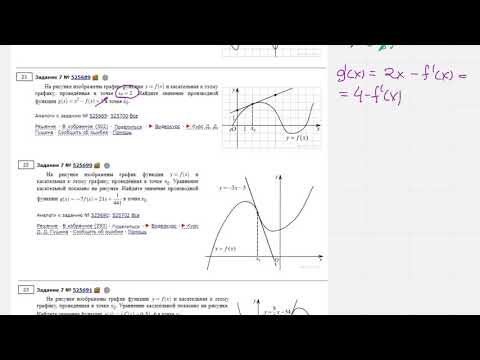
ЕГЭ Математика профиль Задание 7 #525689

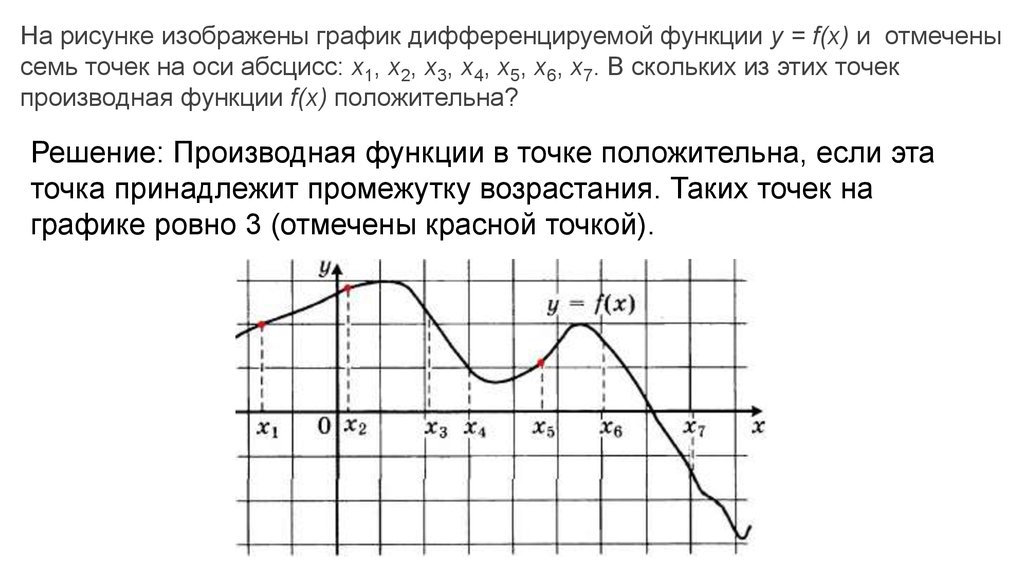
Проверьте значения первой и второй производной функции, чтобы определить, является ли точка критической точкой минимума, максимума или седловой точкой.
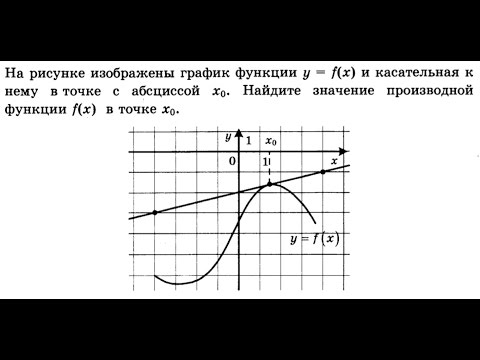
ЕГЭ 2017 Профильный №7 найти производную в точке касания #7
Сравните графики разных функций с одинаковыми производными, чтобы понять, как изменяется форма графика при различных начальных условиях.
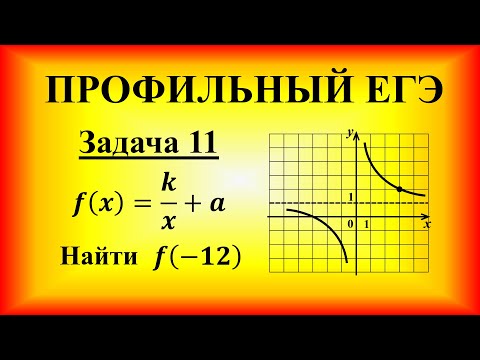
На рисунке изображен график функции f(x)=k/x+a. Найдите f(-12). Профильный ЕГЭ, задача 11.
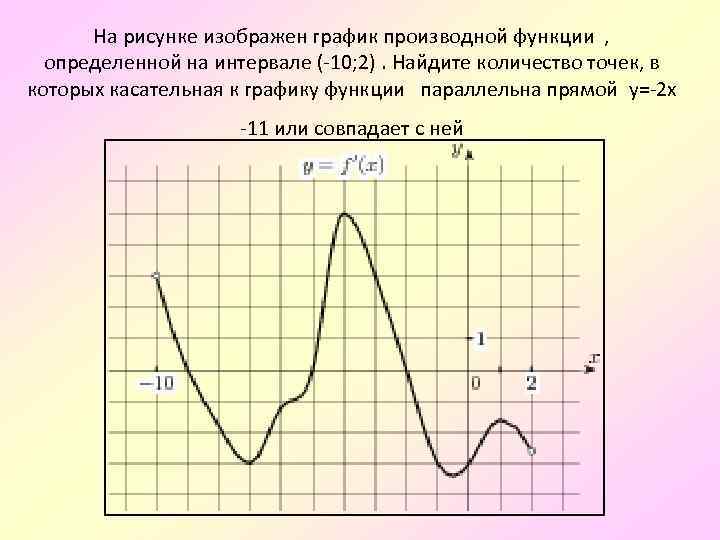
Обратите внимание на асимптоты и их влияние на график функции, чтобы лучше понять, как функция ведет себя на больших и малых значениях переменной.
Практикуйтесь в построении графиков функций и их производных для лучшего понимания их взаимосвязи и поведения.
Используйте компьютерные программы для построения и анализа графиков функций, что поможет увидеть детали, которые трудно заметить вручную.
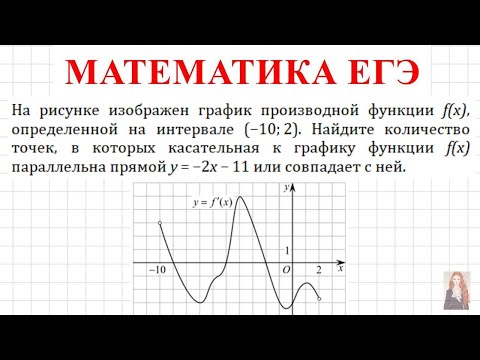
ЕГЭ производная -На рисунке изображен график производной функции f(x), определенной на интервале...

Исследуйте функции с разными степенями полиномов, чтобы увидеть, как изменяется их графическое представление в зависимости от степени.
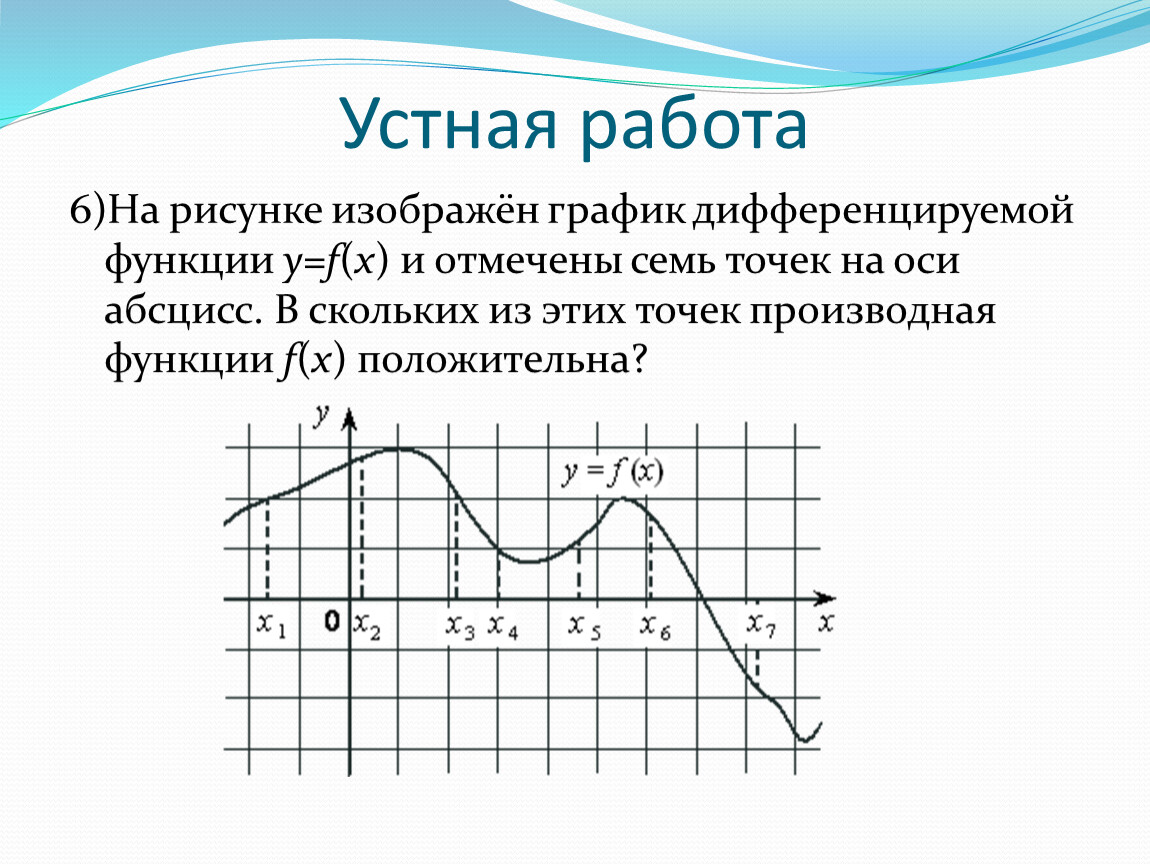

Чтение и интерпретация графиков дифференцируемых функций требует практики, поэтому старайтесь решать как можно больше задач по этой теме.