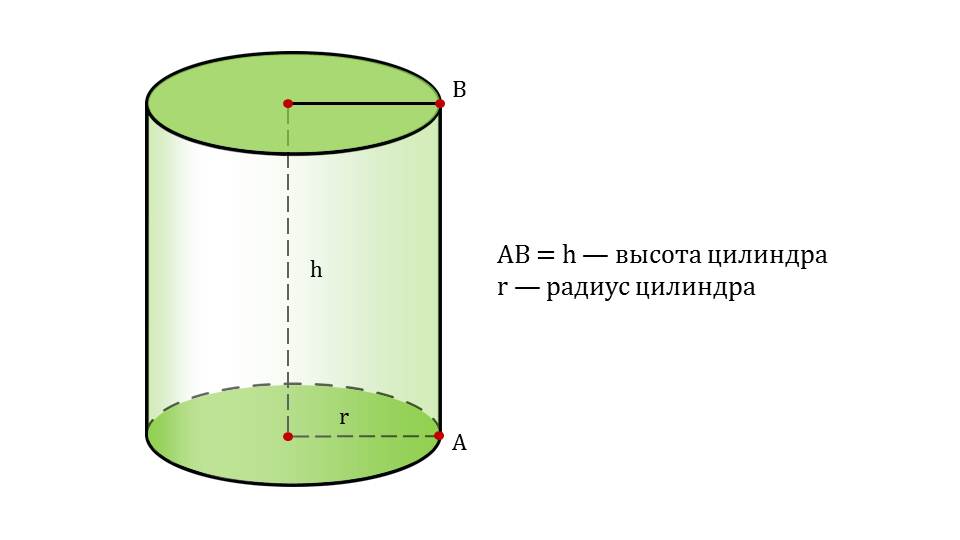
Методы расчета боковой площади цилиндра через радиус основания
В этом разделе вы найдете подробную информацию о том, как рассчитать площадь боковой поверхности цилиндра, зная радиус его основания. Узнайте о необходимых формулах, методах и примерах для правильного вычисления.


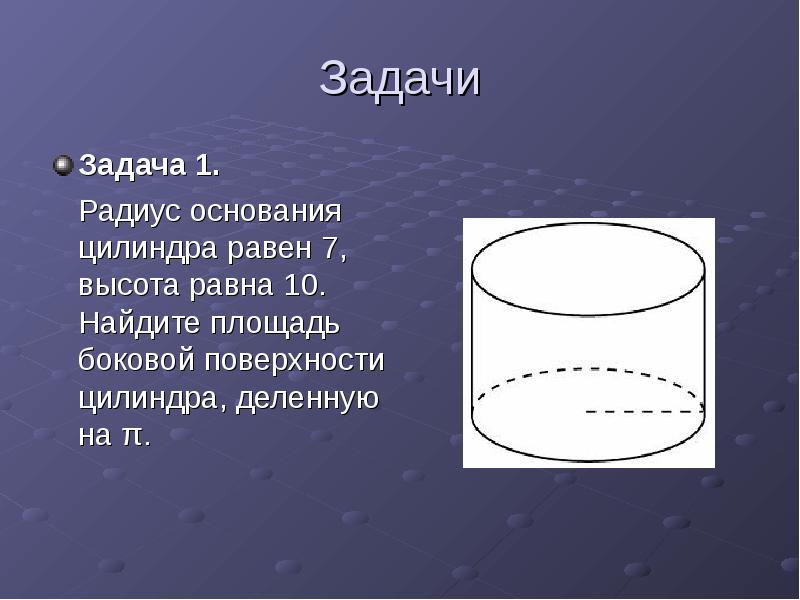
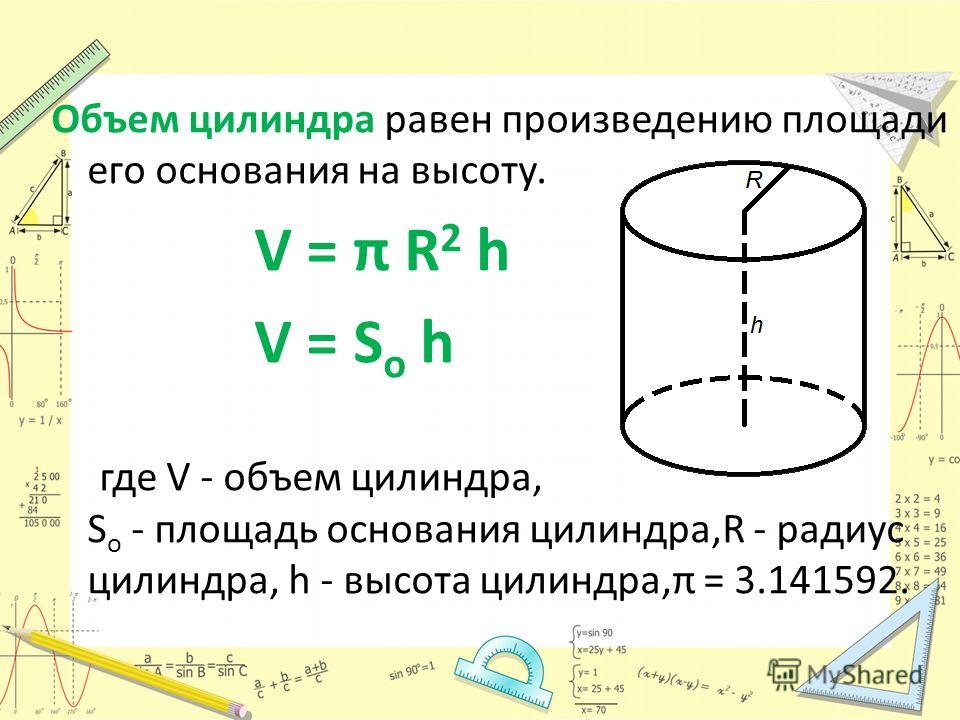
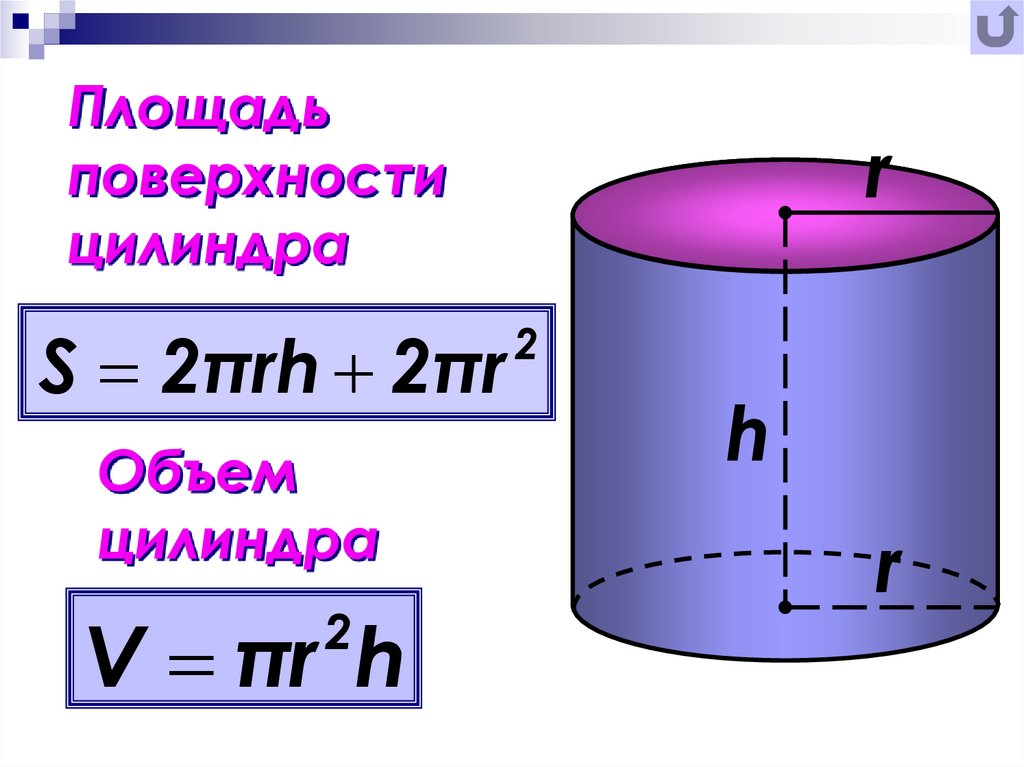
Для расчета площади боковой поверхности цилиндра используйте формулу 2πrh, где r — радиус основания, а h — высота цилиндра.

Цилиндр - расчёт площади, объёма.
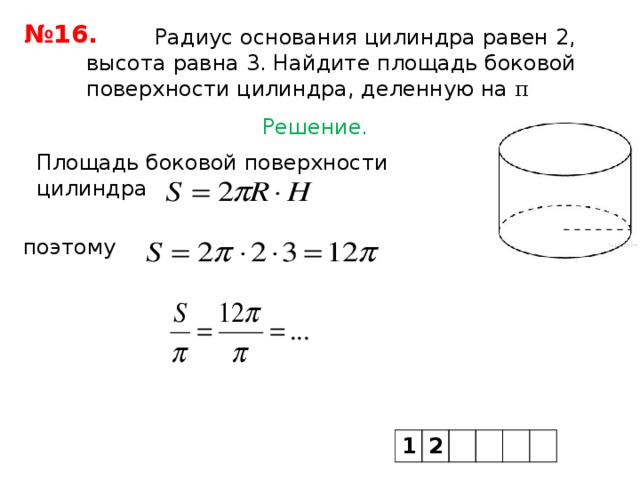
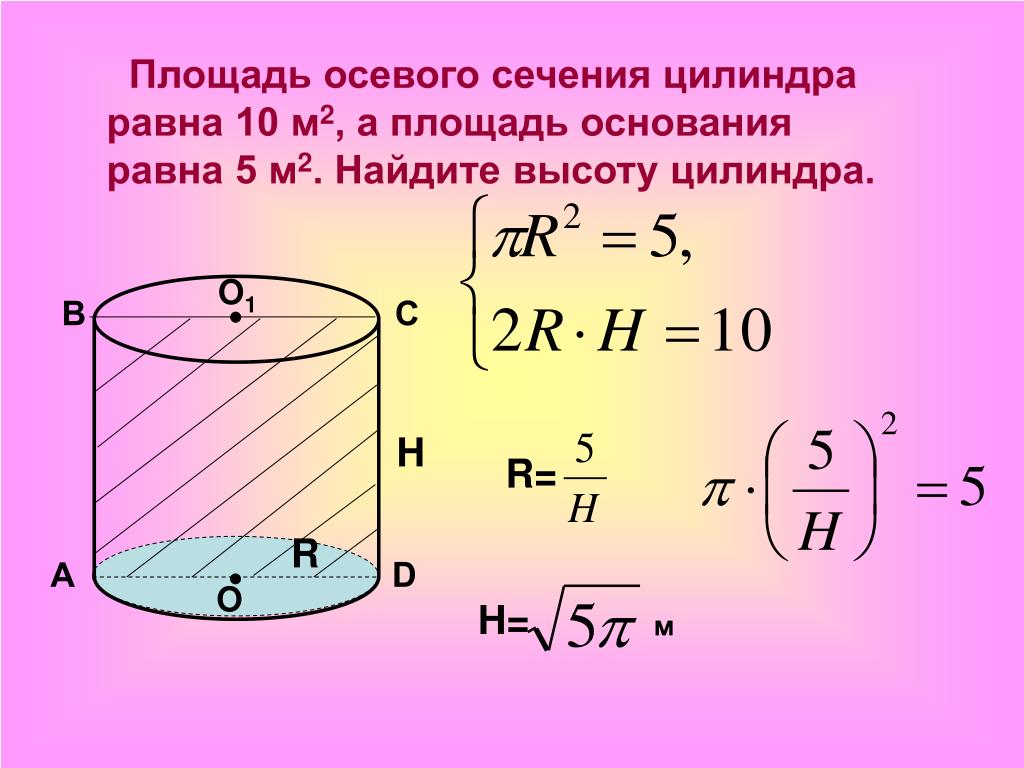
Убедитесь, что радиус и высота цилиндра выражены в одинаковых единицах измерения, чтобы избежать ошибок в расчетах.

Цилиндр. Площадь боковой и полной поверхности цилиндра.


Если вам известен диаметр основания цилиндра, просто разделите его на 2, чтобы найти радиус, и затем используйте формулу для расчета площади.

Видеоурок по математике \

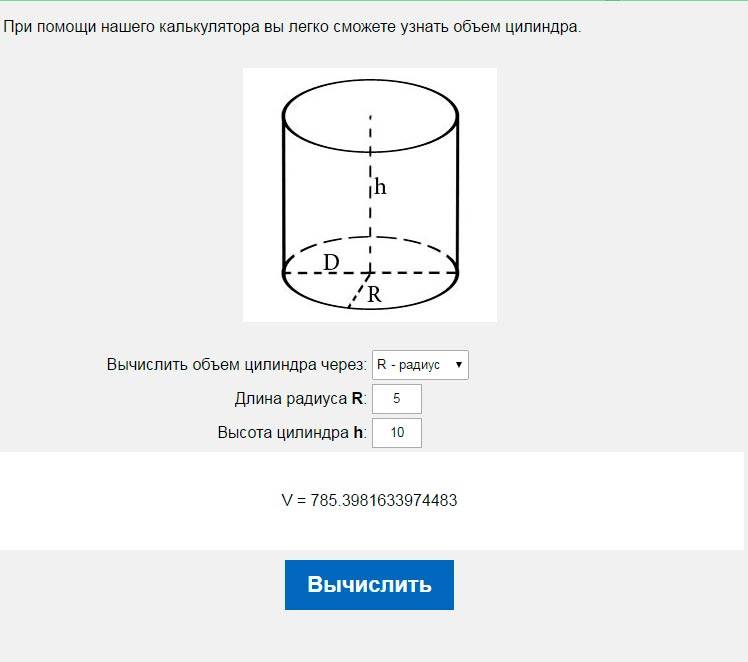
Используйте калькулятор или математическое программное обеспечение для упрощения расчетов и минимизации ошибок при вычислениях.
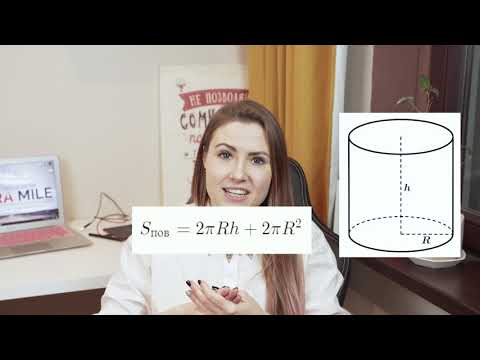
ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРА


При проверке своих расчетов всегда перепроверяйте вводимые значения и убедитесь в правильности используемых формул.

11 класс, 15 урок, Площадь поверхности цилиндра
Изучите графические методы и наглядные примеры для лучшего понимания процесса расчета площади боковой поверхности цилиндра.

Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра
Рассмотрите возможность использования визуальных средств, таких как чертежи и схемы, чтобы легче понимать взаимосвязь между радиусом и высотой цилиндра.

11 artimpression.ru Радиус основания цилиндра равен ,2 высота равна 3 .Найдите площадь боковой поверхности ци
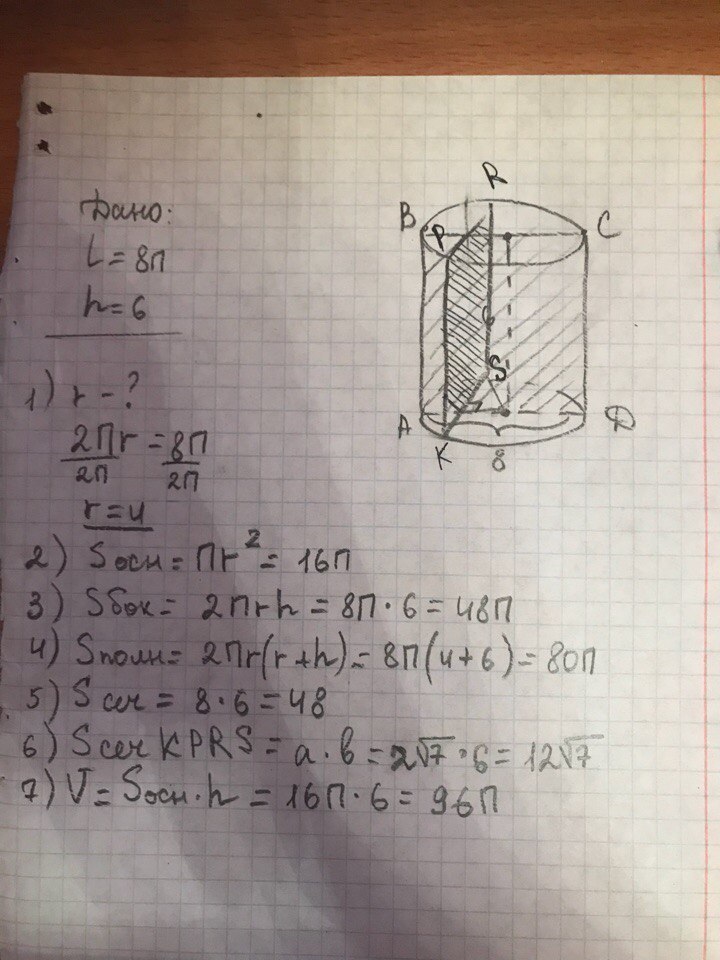

Для более сложных цилиндрических конструкций (например, с уклоном) используйте дополнительные методы и формулы, соответствующие вашему конкретному случаю.

Септик расчёт объёма / Septic tank volume calculations
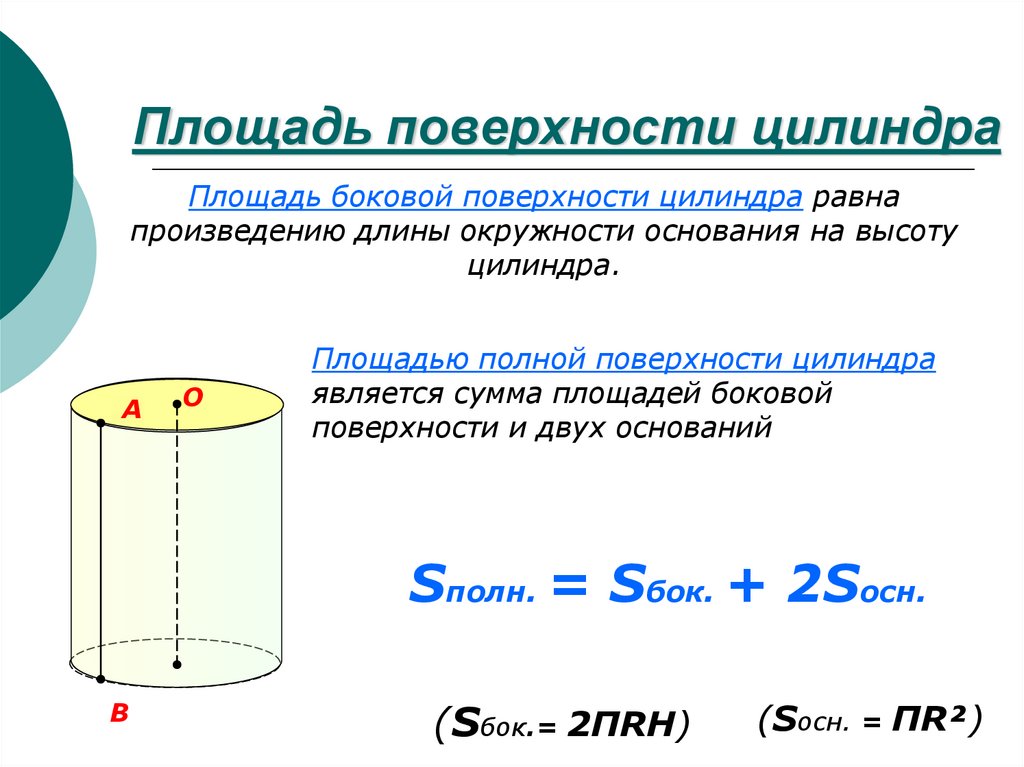
Не забывайте, что точность измерений напрямую влияет на результат. Поэтому используйте точные инструменты и методы измерения.
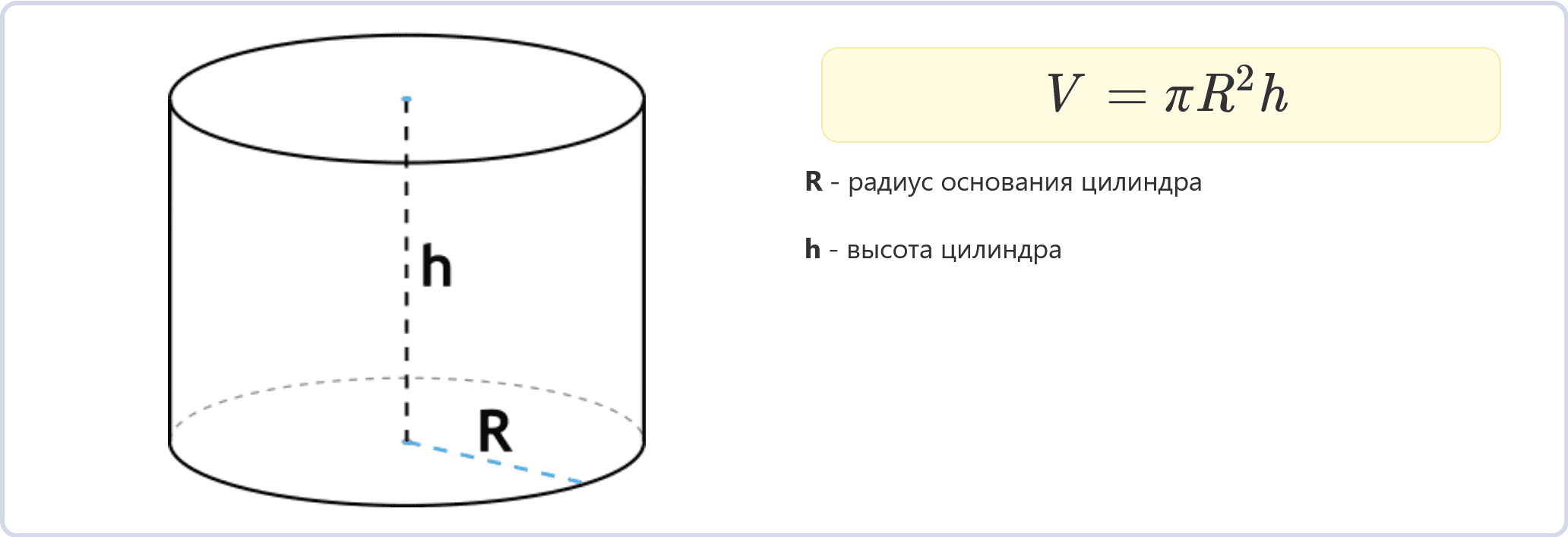
Практикуйтесь на различных примерах, чтобы укрепить свои навыки в расчете площади боковой поверхности цилиндра и уверенно применять формулы.
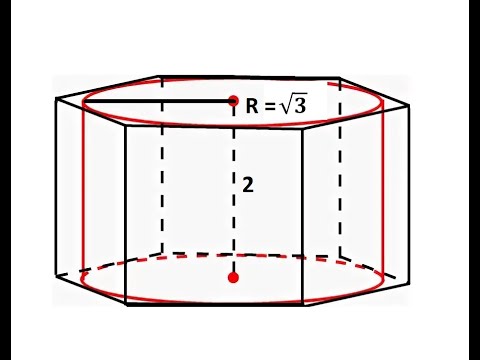
ЕГЭ 2022 математика задача 4 вариант 2