Разбор и применение ограниченных последовательностей в науке и технике

Ограниченная последовательность — это последовательность элементов, которая имеет конечное число значений или ограничена определённым образом. В этом разделе представлены полезные советы и практические рекомендации по использованию и анализу таких последовательностей в различных областях, от математики до компьютерных наук.

Понимание основ ограниченных последовательностей поможет вам в решении задач, связанных с дискретной математикой и программированием.

Используйте графические методы для визуализации ограниченных последовательностей, чтобы лучше понять их свойства и поведение.

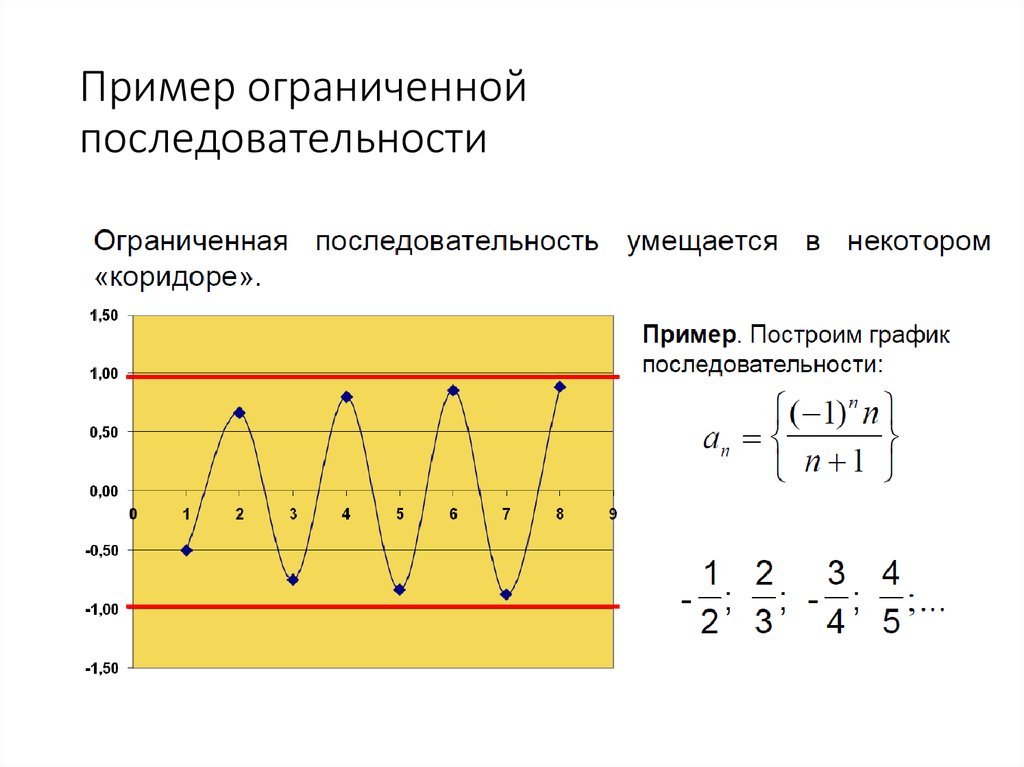
Регулярно практикуйтесь с примерами ограниченных последовательностей, чтобы улучшить свои аналитические навыки.

Применяйте алгоритмические подходы для обработки ограниченных последовательностей в программировании и вычислительных задачах.

Обратите внимание на особенности конечных и бесконечных последовательностей для более глубокого понимания их применения.

Часто используйте специализированные программные инструменты и библиотеки для работы с ограниченными последовательностями.

Изучите теоретические основы, такие как теорема о предельных точках, чтобы расширить свои знания о последовательностях.

Практикуйтесь в решении задач, где ограниченные последовательности играют ключевую роль, чтобы улучшить свою экспертность.

Обсуждайте свои находки и вопросы по ограниченным последовательностям с коллегами или в профессиональных сообществах.

Старайтесь интегрировать изучение ограниченных последовательностей в свой общий образовательный план для достижения комплексных знаний.