Эффективные советы для работы с матрицей в ступенчатой форме
Ступенчатая форма матрицы - это удобный инструмент в линейной алгебре, который помогает упростить систему уравнений и облегчить их решение. В этом руководстве вы найдете полезные советы и инструкции по созданию и использованию ступенчатой формы матрицы.
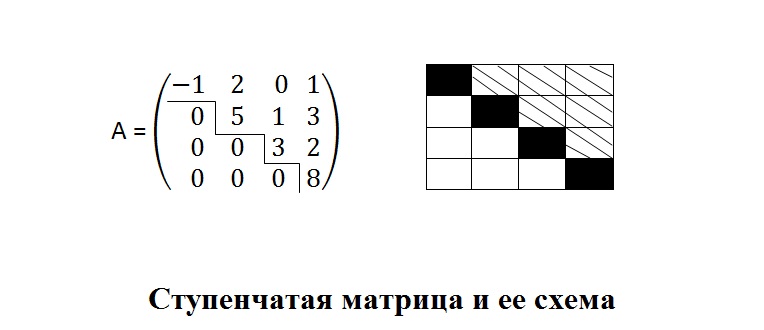


Начинайте с преобразования вашей матрицы в треугольную форму с помощью элементарных преобразований строк.

Как привести матрицу к ступенчатому виду - bezbotvy

Убедитесь, что главный элемент (первый ненулевой элемент строки) в каждой строке равен единице.

Lecture#130:Diagonalization of a Square Matrix
Переставляйте строки, чтобы главный элемент каждой следующей строки был расположен правее предыдущего.
Find Rank of a Matrix in Seconds
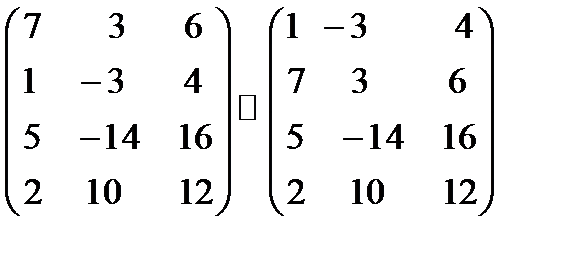
Если главный элемент в строке равен нулю, переставьте строки или используйте линейные комбинации, чтобы получить ненулевой элемент.

Виды матриц: транспонированная, диагональная, скалярная, ступенчатая, обратная, вырожденная
Используйте обратные элементарные преобразования строк для приведения матрицы к ступенчатой форме.

Приведение матрицы к ступенчатому виду

Проверяйте каждый шаг для избегания ошибок в вычислениях и корректности преобразований.

Математика без Ху%!ни. Метод Гаусса. Совместность системы. Ранг матрицы.
После приведения матрицы к ступенчатой форме, проверьте ее на наличие свободных переменных.

Используйте обратные ходы для нахождения решений системы уравнений, если это требуется.
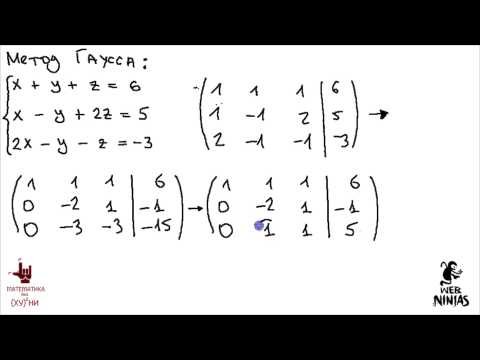
Математика без Ху%!ни. Метод Гаусса.

Запоминайте типичные формы и методы преобразования для упрощения процесса.

Практикуйтесь на разных примерах матриц, чтобы лучше понять и освоить метод.

Матрицы ступенчатого вида 1

Элементарные преобразования матриц. Высшая математика.