Как работать с множествами: советы и хитрости
Множества - фундаментальная концепция математики, которая играет важную роль в различных областях науки и техники. В этой подборке вы найдете фотографии и полезные советы, которые помогут вам лучше понять и использовать свойства множеств в ваших проектах.



Начните с основ: определите, что такое множество и как оно используется в математике.

Свойства действий над множествами


Изучите различные типы множеств, такие как конечные, бесконечные, подмножества и пересечения.

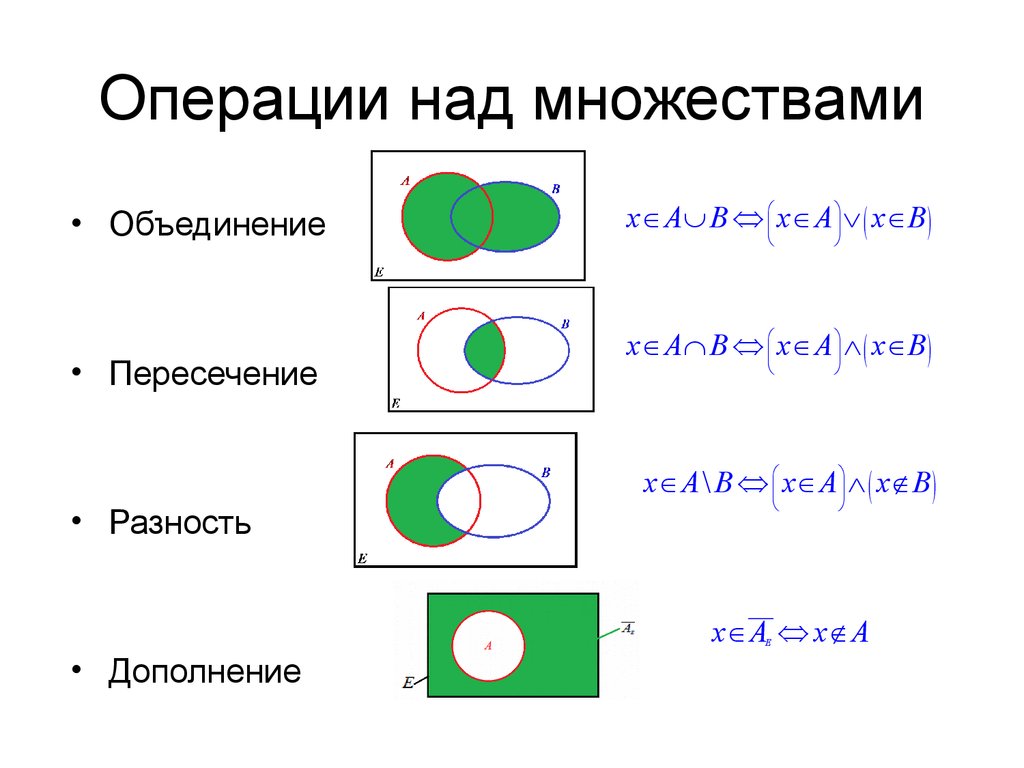
Операции над множествами

Практикуйте операции над множествами: объединение, пересечение, разность и дополнение.

Подмножество. Операции над множествами (пересечение, объединение множеств) – 8 класс алгебра

Используйте диаграммы Венна для визуализации отношений между множествами.

Множества и операции над ними

Изучите законы и теоремы, связанные с множествами, такие как законы Де Моргана.

Теория групп 2. Сопряжённость. Нормальная подгруппа. Гомоморфизм групп

Применяйте множества в задачах по комбинаторике и теории вероятностей.

Аппроксимативные свойства множеств

Понимайте связь множеств с функциями и отношениями в математике.

Используйте программные инструменты и языки программирования для работы с множествами.

Проверяем свойства отношений

Отображения множеств

Практикуйтесь на реальных примерах и задачах, чтобы лучше усвоить материал.


Поддерживайте свои знания актуальными, читая современные исследования и статьи по теме множеств.


Пересечение множеств. Объединение множеств. 5 класс.