Как разложить вектор по трём некомпланарным векторам: теорема и её применение
В этом разделе мы рассмотрим теорему о разложении вектора по трём некомпланарным векторам. Эта теорема является важной частью линейной алгебры и позволяет представить любой вектор в пространстве через линейные комбинации трёх некомпланарных векторов, которые образуют базис. Мы предоставим подробные объяснения, примеры и графические иллюстрации, чтобы сделать понимание теоремы более доступным.


Для успешного применения теоремы важно убедиться, что выбранные векторы действительно некомпланарны. Это можно проверить, убедившись, что определитель матрицы из этих векторов не равен нулю.

10 класс, 45 урок, Разложение вектора по трем некомпланарным векторам

При работе с разложением вектора по некомпланарным векторам полезно использовать матричные методы для вычисления коэффициентов разложения. Это упростит и ускорит процесс.

Как выражать вектор? Как решать задачу с вектором? - TutorOnline

Внимательно проверяйте вычисления при разложении вектора, так как ошибки в арифметике могут привести к неверным результатам. Используйте калькулятор или программное обеспечение для повышения точности.

Разложение вектора по базису. 9 класс.

Графическое представление разложения вектора поможет лучше понять концепцию. Постройте векторы и их комбинации на координатной плоскости для визуализации процесса.

Олегу Тинькову* запрещён вход на Мехмат МГУ

Если вы столкнулись с трудностями, попробуйте сначала разложить вектор по двум некомпланарным векторам, а затем добавить третий вектор для проверки результата.

Найдите разложение вектора по векторам (базису)
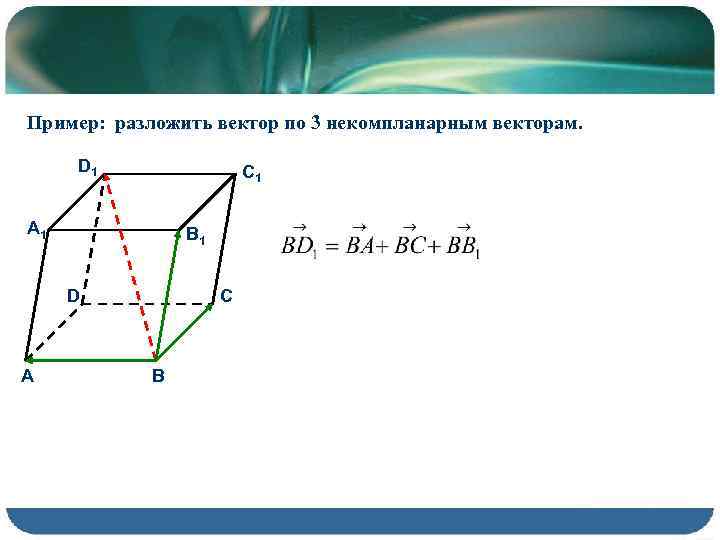
Обратите внимание на единичные векторы и их комбинации. Они могут упростить задачи разложения и дать более ясное представление о структуре векторного пространства.

РАЗЛОЖЕНИЕ ВЕКТОРА по трем векторам
Используйте примеры из реальных задач для практики разложения векторов. Это поможет лучше понять, как применяются теоретические знания на практике.

Разложение вектора по трем некомпланарным векторам
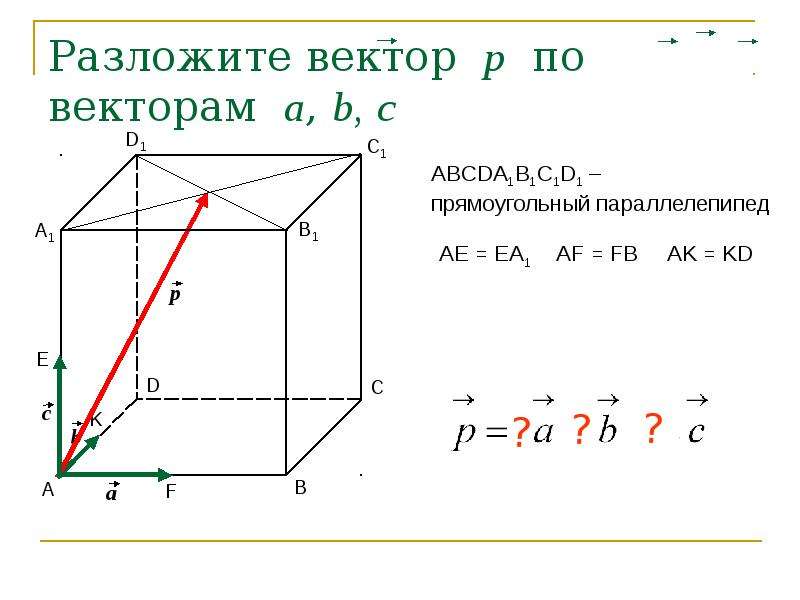
Для более глубокого понимания теоремы изучите её доказательства и различные варианты её применения в различных областях математики и физики.
Устная задача с собеседования в МФТИ

Регулярно повторяйте и практикуйте задачи, связанные с разложением векторов, чтобы закрепить теоретические знания и развить практические навыки.
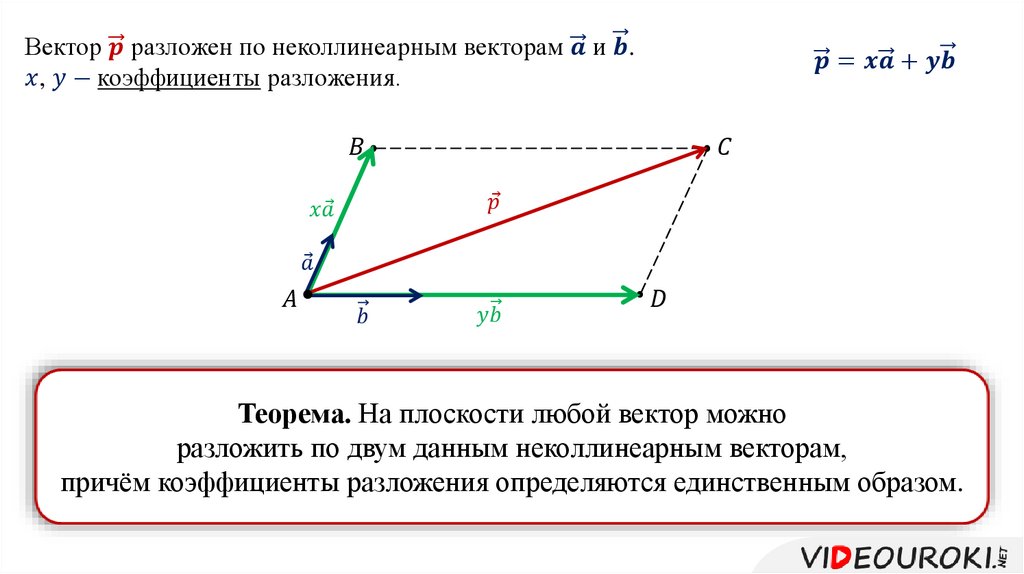

При изучении теоремы не забывайте про её связь с другими математическими концепциями, такими как линейная независимость и базис пространства, чтобы видеть более полную картину.