Введение в теорию вероятностей: что нужно знать вкратце

Теория вероятностей изучает случайные явления и помогает понять, как предсказать результаты случайных событий. В этой статье вы найдете краткое введение в основные понятия теории вероятностей, которые помогут вам лучше разобраться в этой области и применять полученные знания на практике.

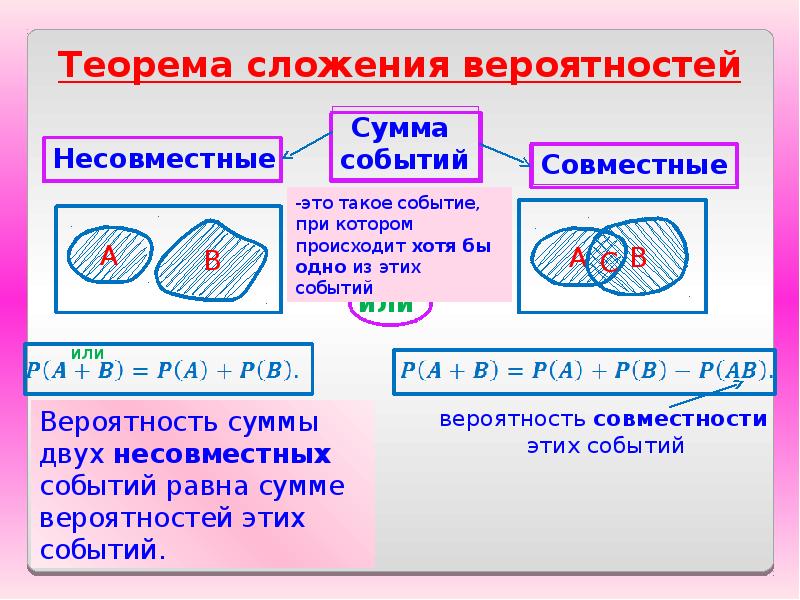
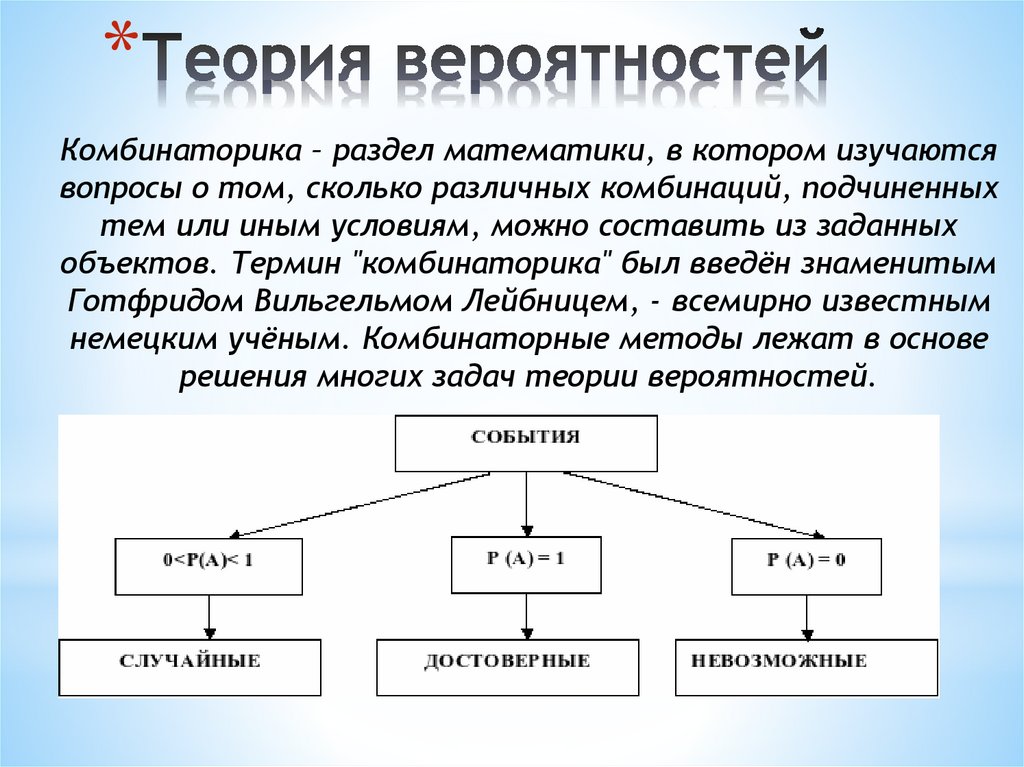
Начните с изучения базовых понятий, таких как случайные события, вероятность и законы сложения и умножения вероятностей.

Используйте графические методы, такие как диаграммы Венна, для визуализации и лучшего понимания взаимосвязей между событиями.

Изучите различные распределения вероятностей, такие как нормальное и биномиальное, чтобы понимать, как они моделируют реальные случайные явления.

Практикуйтесь в решении задач и применении теории вероятностей к реальным ситуациям, чтобы закрепить свои знания.

Используйте онлайн-ресурсы и калькуляторы для проверки своих расчетов и получения дополнительной практики.

Обратитесь к учебным пособиям и лекциям, чтобы углубить свои знания в этой области и узнать о последних достижениях в теории вероятностей.

Регулярно решайте задачи на вероятность, чтобы поддерживать и улучшать свои навыки в этой области.

При изучении более сложных тем, таких как статистическая вероятность и условная вероятность, не забывайте обращаться к основам.

Задавайте вопросы и ищите ответы на форумах и в учебных группах, чтобы разобраться в трудных моментах.

Не бойтесь делать ошибки – они являются важной частью процесса обучения и помогут вам лучше понять материал.