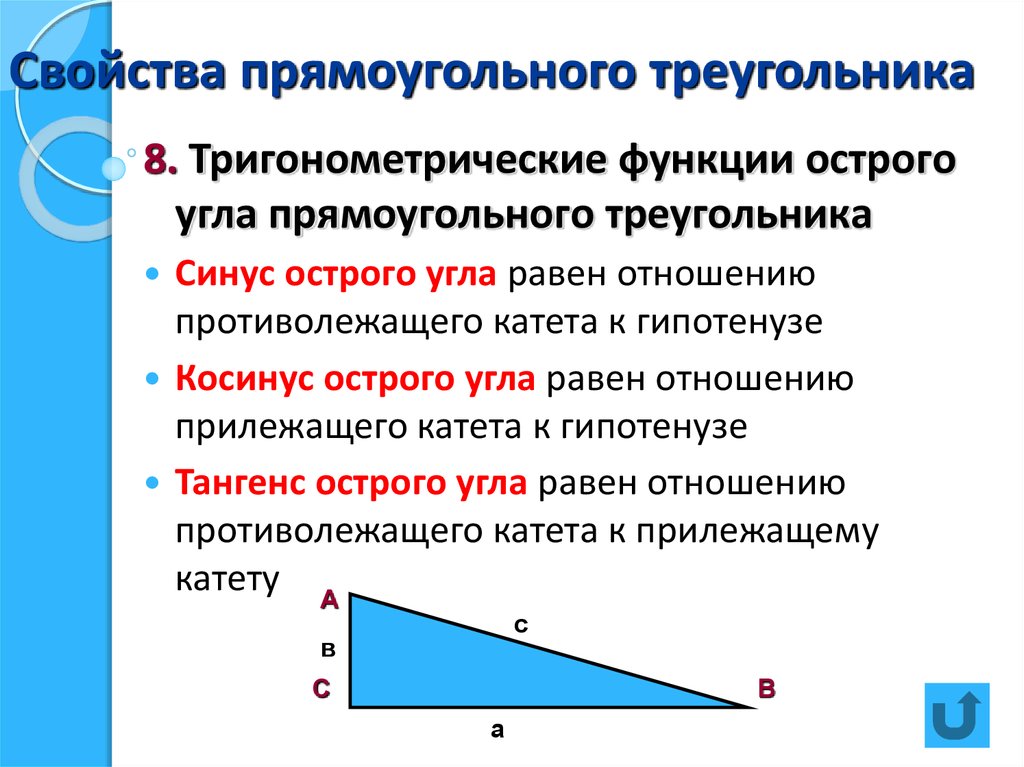
Тригонометрические соотношения и их применение в прямоугольных треугольниках
Изучите ключевые тригонометрические соотношения в прямоугольных треугольниках, которые помогут вам решать задачи и применять знания в практике. В этой подборке представлены полезные советы и иллюстрации для лучшего понимания темы.
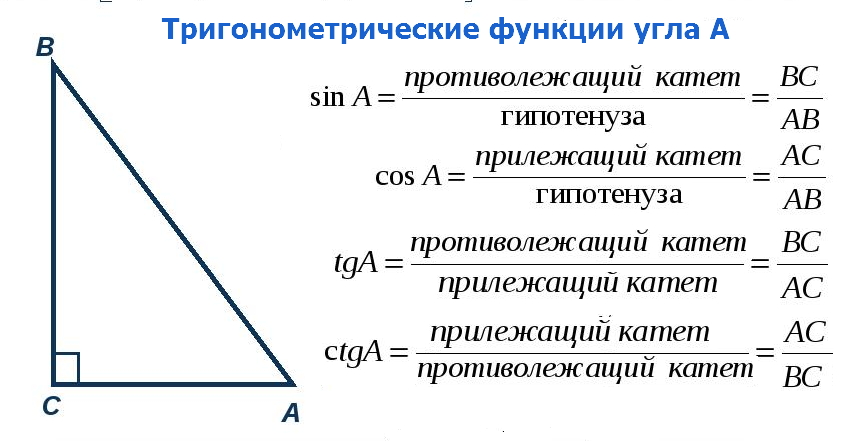
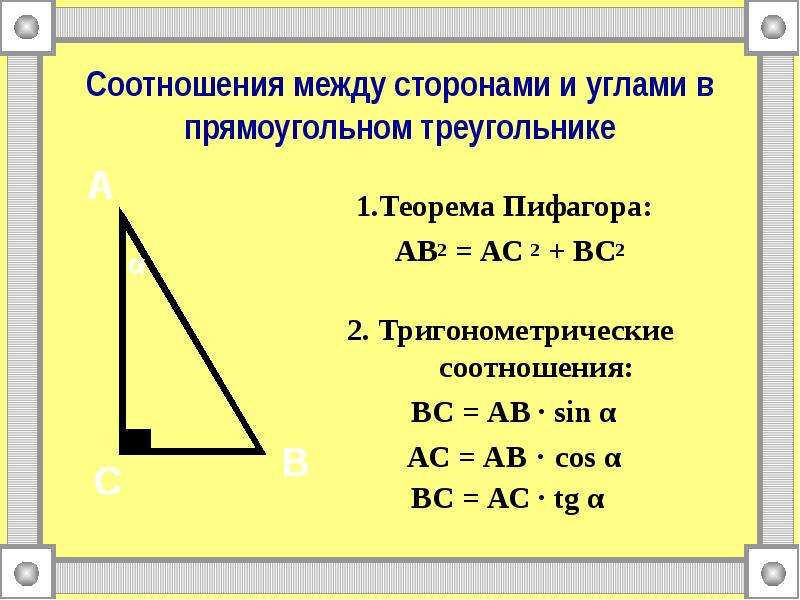

Начните изучение с основных тригонометрических функций: синус, косинус и тангенс. Понимание их определения и взаимосвязей значительно упростит дальнейшее изучение.

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия - Математика

Изучите тригонометрические соотношения для прямоугольных треугольников: основной теорема Пифагора и соотношения для углов 30°, 45° и 60°.

ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого угла
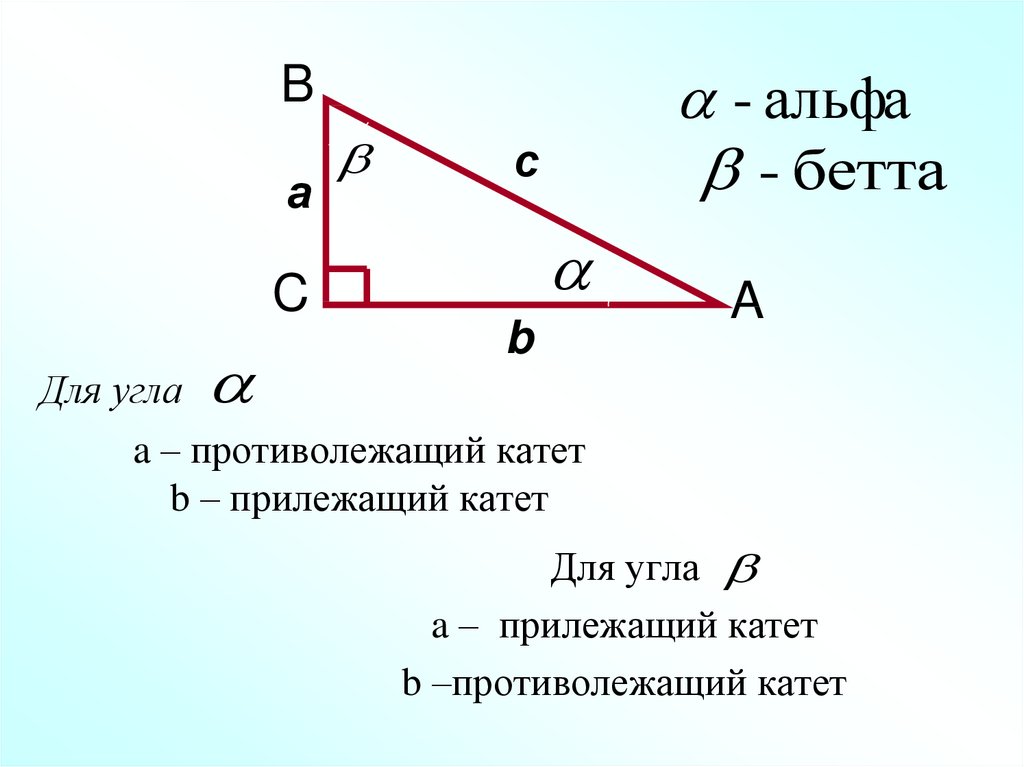
При решении задач на нахождение сторон треугольника используйте таблицы значений тригонометрических функций для ускорения вычислений.

8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольника
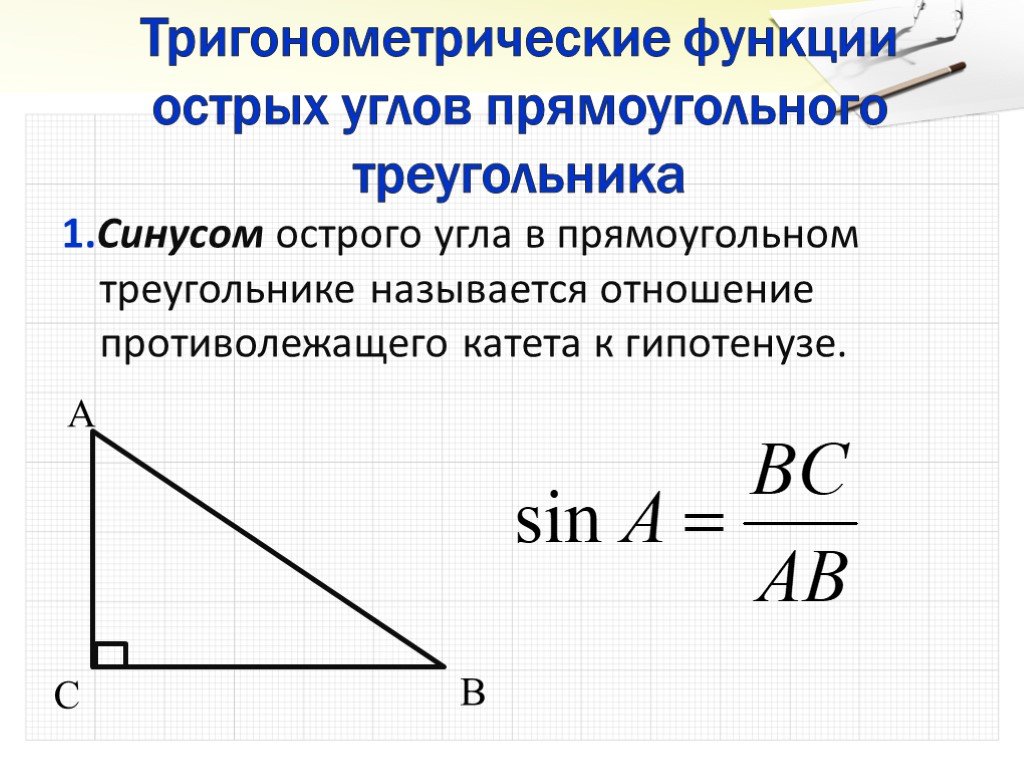
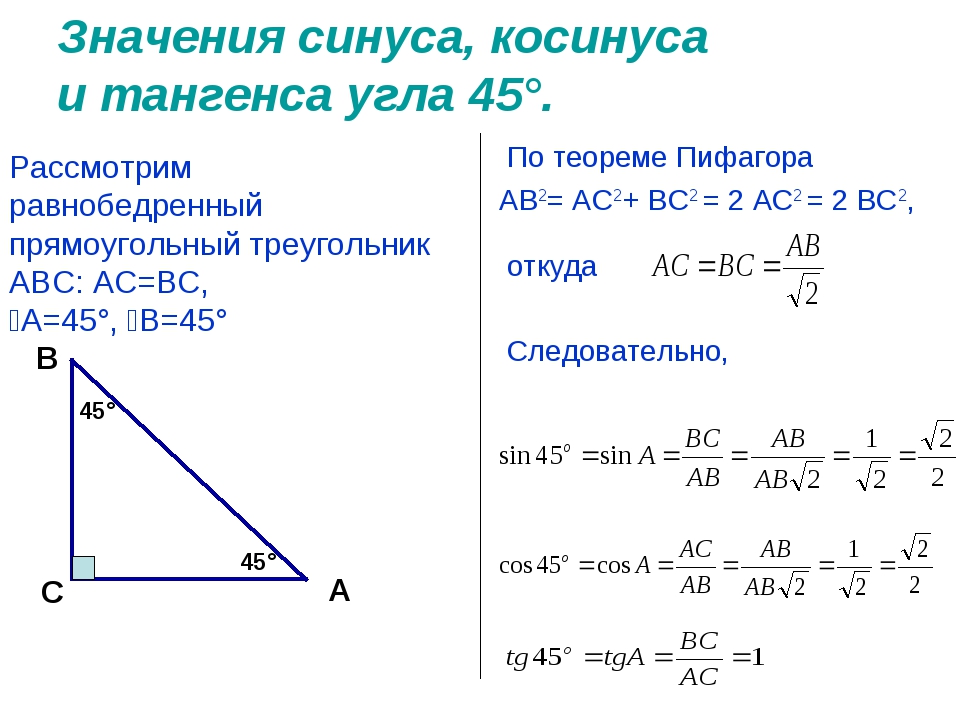
Практикуйтесь в решении задач с различными уровнями сложности. Это поможет закрепить понимание тригонометрических соотношений.
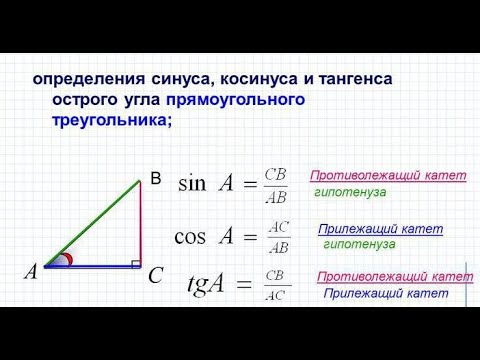
Решение прямоугольных треугольников. Синус, косинус, тангенс, котангенс. Решение задач
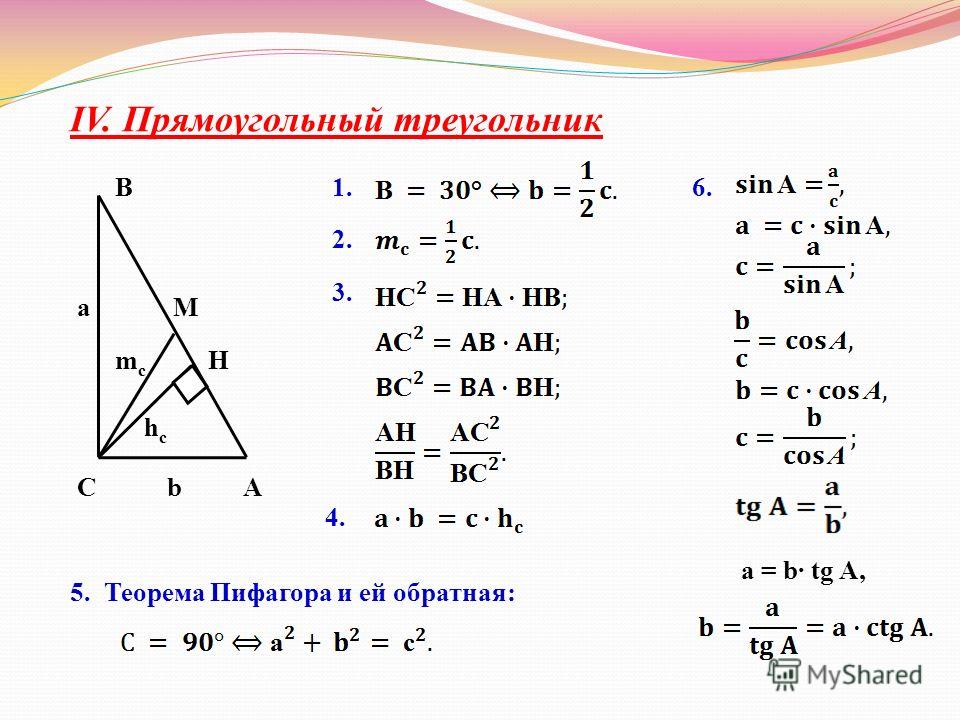
Используйте визуализацию: рисуйте треугольники и отмечайте углы и стороны для наглядного понимания соотношений.

Основное тригонометрическое тождество. 8 класс.


Обратите внимание на единицы измерения углов: в некоторых задачах необходимо использовать градусы, в других — радианы.

Математика - Соотношения между сторонами и углами в прямоугольном треугольнике.
При решении задач на нахождение углов используйте обратные тригонометрические функции: арксинус, арккосинус и арктангенс.

Геометрия 8. Урок 11- Синус, Косинус, Тангенс и Котангенс угла в прямоугольном треугольнике.
Помните о формуле для нахождения высоты прямоугольного треугольника через его стороны и углы.
Высота в прямоугольном треугольнике - Математика ЕГЭ 2024 #математика #профиль #егэ #егэпрофиль

ТРИГОНОМЕТРИЯ - Синус, Косинус, Тангенс, Котангенс

Практикуйтесь с различными типами задач: от простых до более сложных, чтобы развить глубокое понимание тригонометрических соотношений.

Синус, косинус, тангенс, котангенс за 5 МИНУТ
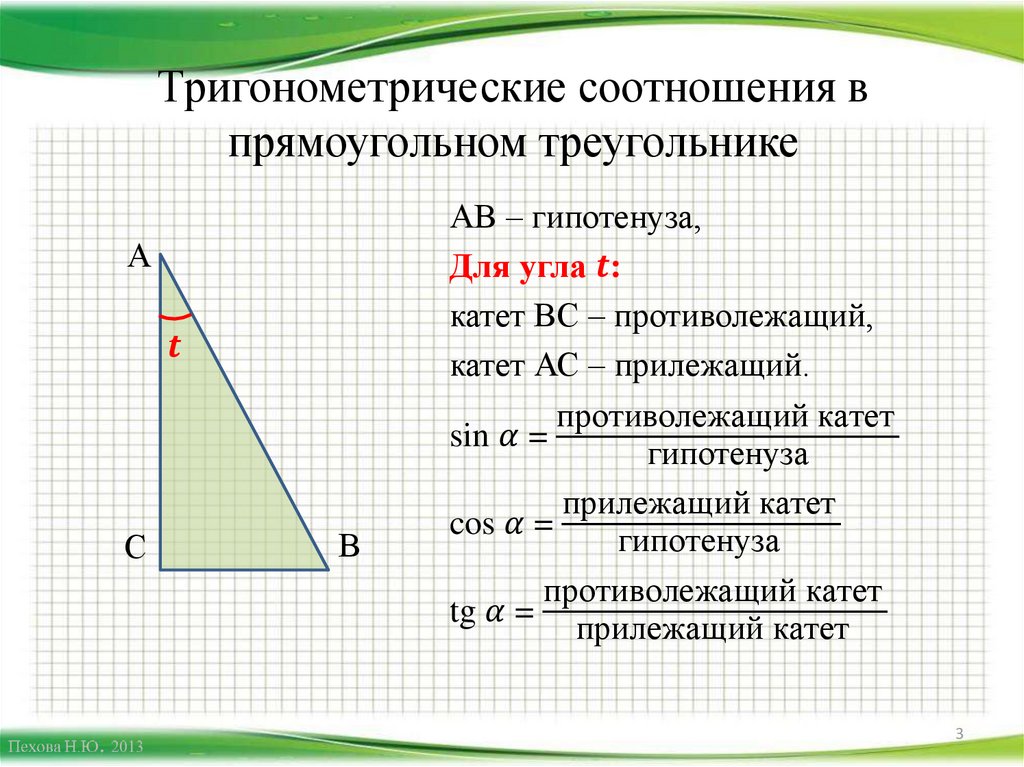
Не забывайте проверять результаты расчетов и использовать альтернативные методы решения для проверки правильности.