Пошаговое руководство по нахождению уравнения касательной параллельной прямой
В этой статье мы рассмотрим, как находить уравнение касательной, которая параллельна заданной прямой. Это важная тема в математике, особенно в области дифференциального исчисления и аналитической геометрии. Мы предоставим вам подробные объяснения и примеры, чтобы вы могли лучше понять, как решать такие задачи.


Определите уравнение прямой, параллельной которой будет касательная. Обратите внимание на её наклон (коэффициент перед x).

10 класс, 43 урок, Уравнение касательной к графику функции

Найдите производную функции, к графику которой необходимо провести касательную. Это поможет вам определить наклон касательной.

уравнение касательной

Приравняйте наклон касательной к наклону заданной прямой. Это обеспечит параллельность прямых.

ВЫСШАЯ МАТЕМАТИКА. 9.12. Уравнение касательной, параллельной прямой вида y=kx+b


Подставьте точку касания в уравнение касательной, чтобы определить её полный вид.

Уравнение касательной

Убедитесь, что найденное уравнение касательной имеет тот же наклон, что и заданная прямая.

Прямая y=8x+11 параллельна касательной к графику функции y=x^2+7x-7. Найдите абсциссу точки касания.


Используйте производную второго порядка для проверки касательной, если это необходимо для дополнительной точности.
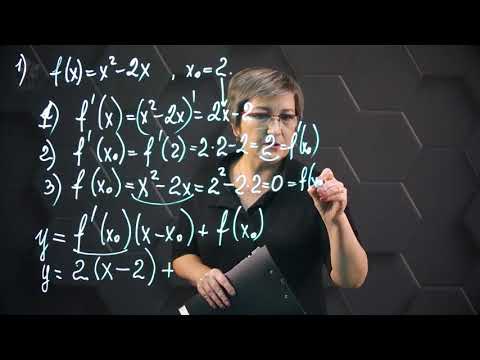
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.

Практикуйтесь на различных примерах, чтобы лучше освоить методику нахождения касательных.

Урок 13. Уравнение касательной, проходящей параллельно прямой. Производные. Алгебра 10, 11 класс.

Визуализируйте графики функций и касательных, чтобы получить лучшее понимание проблемы.
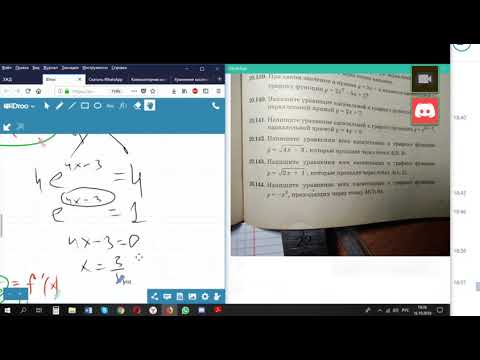
Уравнение касательной параллельной прямой Д160
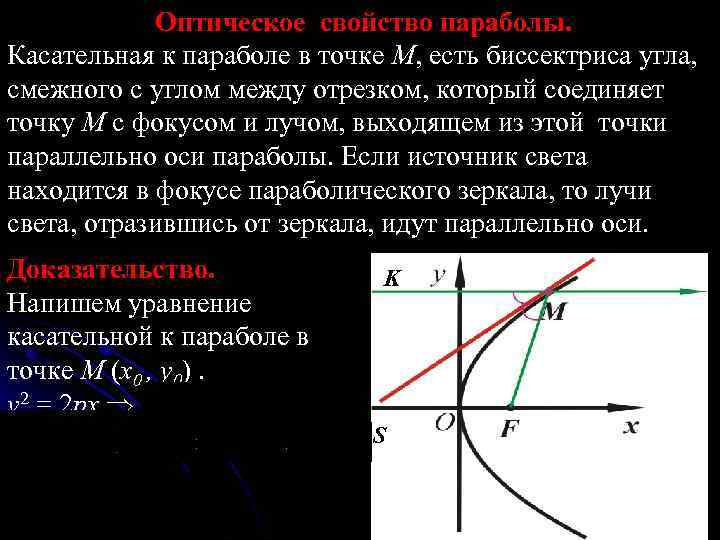
Изучите связанные темы, такие как уравнения нормалей, чтобы углубить свои знания.

Помните, что касательная всегда касается графика функции только в одной точке, что делает её уникальной для каждой функции.

Производная: касательная параллельная к заданной.
