Уравнение для нахождения стороны треугольника по координатам точек
В этой статье мы рассмотрим, как найти длину стороны треугольника, используя координаты его вершин. Подробное объяснение и полезные советы помогут вам без труда справиться с этой задачей.


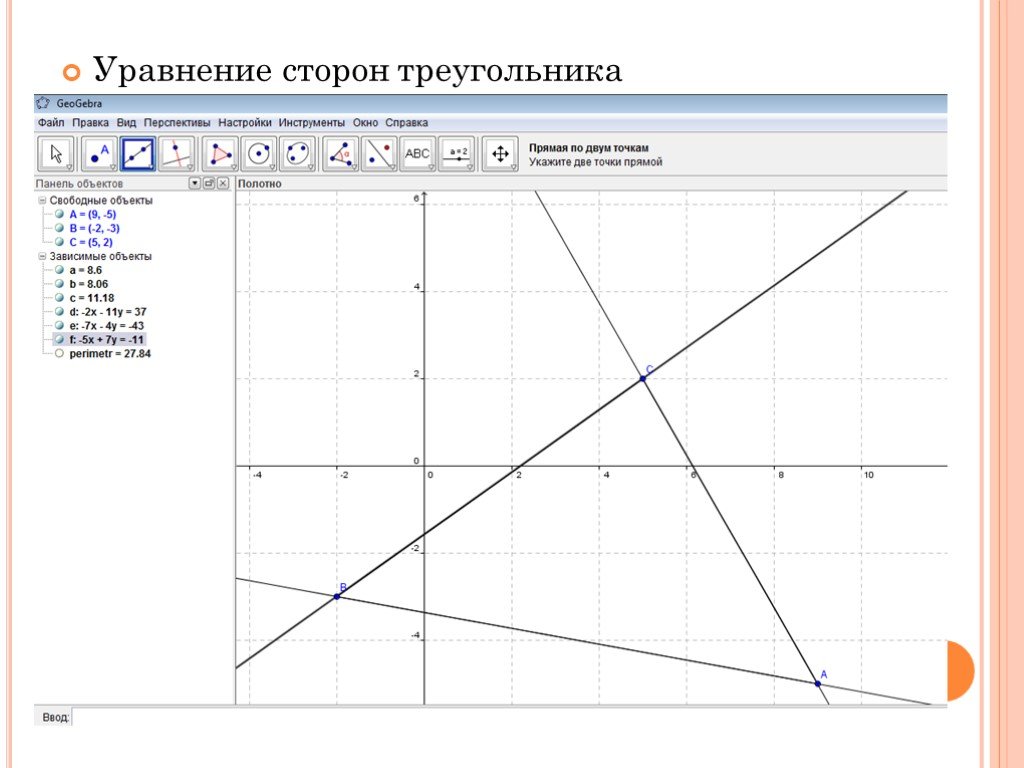
Убедитесь, что вы правильно определили координаты всех вершин треугольника перед началом вычислений.
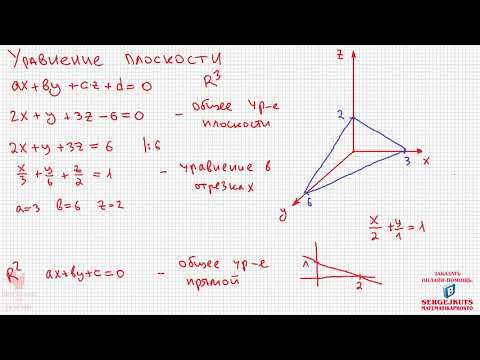
Математика без Ху%!ни. Уравнение плоскости.

Используйте формулу расстояния между двумя точками для расчета длины стороны.

Самый короткий тест на интеллект Задача Массачусетского профессора

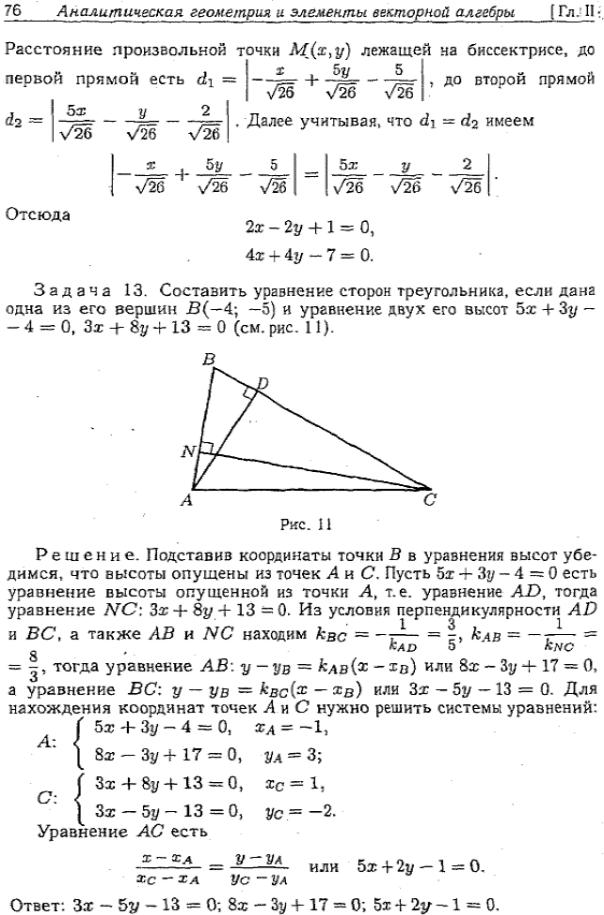
Проверьте точность вычислений, пересчитав каждую сторону несколько раз.

Аналитическая геометрия, 6 урок, Уравнение прямой

Если у вас есть графический калькулятор, используйте его для проверки результатов.

найти уравнение высоты треугольника
Помните, что все вычисления должны быть выполнены с одинаковой точностью (например, до двух знаков после запятой).
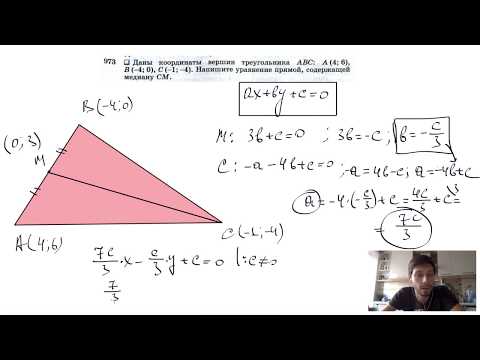
№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнение


Если вы работаете с задачей в школьном контексте, не забывайте объяснять каждый шаг решения.
Не забывайте учитывать единицы измерения, если они указаны в задаче.
Для удобства вы можете строить график, чтобы визуально убедиться в правильности найденных длин сторон.

Уравнение прямой и треугольник. Задача про высоту
При работе с большими числами будьте внимательны к знакам и порядку выполнения операций.
Проверьте результаты вычислений, используя альтернативные методы, такие как тригонометрия.
