Советы и методы для нахождения вершины гиперболы
На этой странице вы найдете подборку фотографий и полезные советы по нахождению вершины гиперболы, а также сможете лучше понять ее уравнение и свойства.


Определите вид уравнения гиперболы, так как это поможет понять, с каким типом гиперболы вы имеете дело.

Всё о квадратичной функции. Парабола - Математика TutorOnline
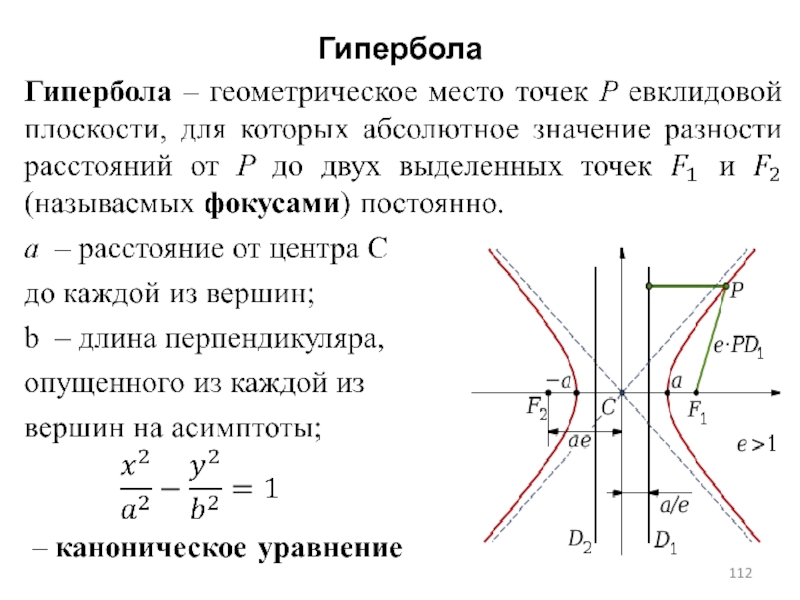

Запомните, что гипербола может иметь уравнение вида x²/a² - y²/b² = 1 или y²/a² - x²/b² = 1.
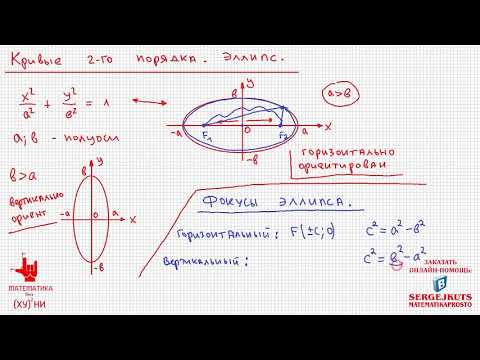
Математика без Ху%!ни. Кривые второго порядка. Эллипс.

Для нахождения вершины гиперболы в каноническом виде уравнения, ищите точки пересечения гиперболы с осями координат.

Парабола, эллипс, гипербола - уравнение при вершине - Лекции по аналитической геометрии

Если уравнение гиперболы имеет форму x²/a² - y²/b² = 1, вершины будут на оси x, в точках (±a, 0).

ПАРАБОЛЫ И ГИПЕРБОЛЫ НА ИЗИ


Если уравнение гиперболы имеет форму y²/a² - x²/b² = 1, вершины будут на оси y, в точках (0, ±a).

Неполное уравнение второго порядка. Эллипс, гипербола. Задачи

Помните, что константы a и b определяют форму и размеры гиперболы, что важно при определении ее вершины.

Используйте графическое построение для более наглядного понимания расположения вершины гиперболы.
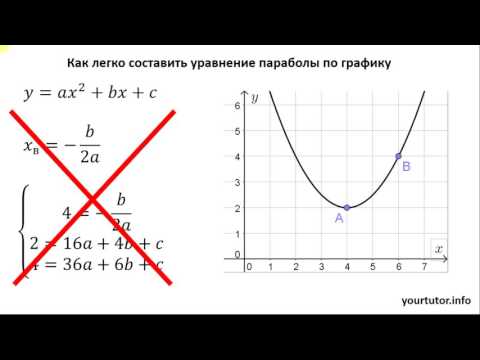
Как легко составить уравнение параболы из графика
При решении задач, связанных с гиперболами, всегда проверяйте правильность вычислений, чтобы избежать ошибок.
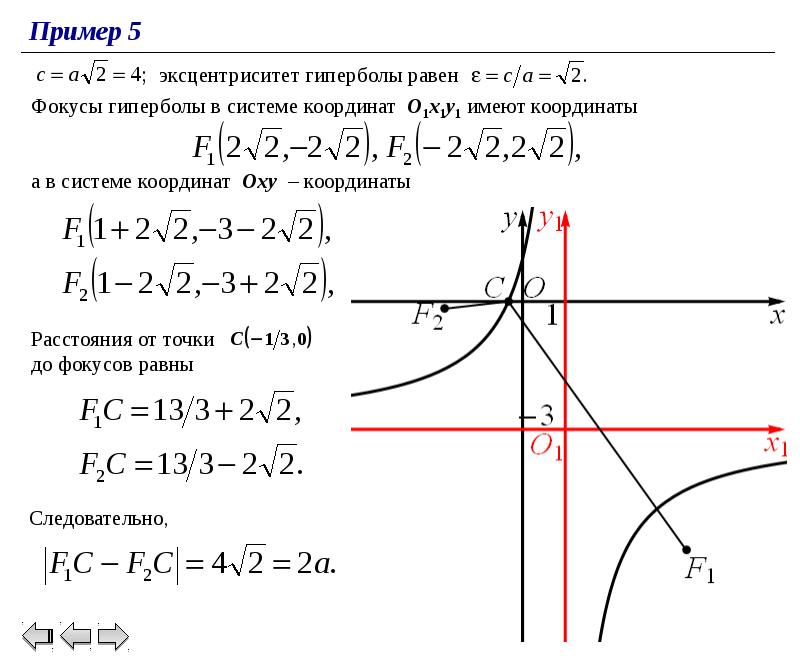
Если уравнение гиперболы задано не в каноническом виде, преобразуйте его с помощью алгебраических методов.

Видеоурок \


Для более сложных уравнений гипербол используйте программное обеспечение для автоматизации вычислений и построений.


Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математика