Обзор вертикальных асимптот и их математическое значение
Вертикальные асимптоты играют важную роль в графическом анализе функций. Они помогают определить, как функция ведет себя при приближении к определенным значениям переменной, где функция стремится к бесконечности. В этом руководстве мы рассмотрим основные принципы вертикальных асимптот и их значение для анализа графиков функций.
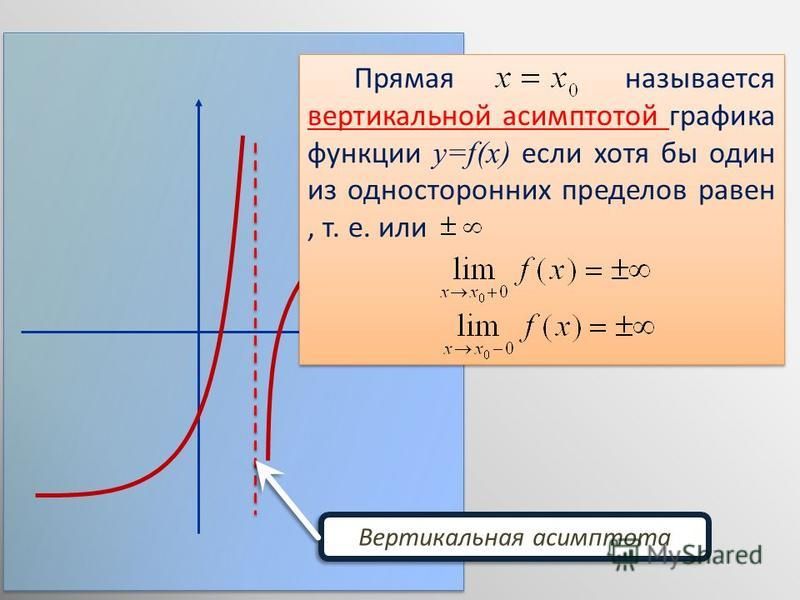

Определите вертикальные асимптоты, исследуя предел функции при стремлении переменной к конкретным значениям.
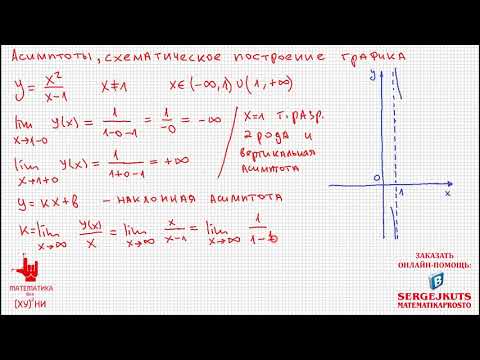
Математика без Ху%!ни. Нахождение асимптот, построение графика функции.


Используйте графическое представление функции для визуализации поведения вблизи вертикальных асимптот.

Асимптоты графика функции. Практика. Пример 1.
Помните, что вертикальная асимптота возникает, когда функция стремится к бесконечности или минус бесконечности при приближении к определенному значению переменной.
Асимптоты функции. Горизонтальная асимптота. 10 класс.
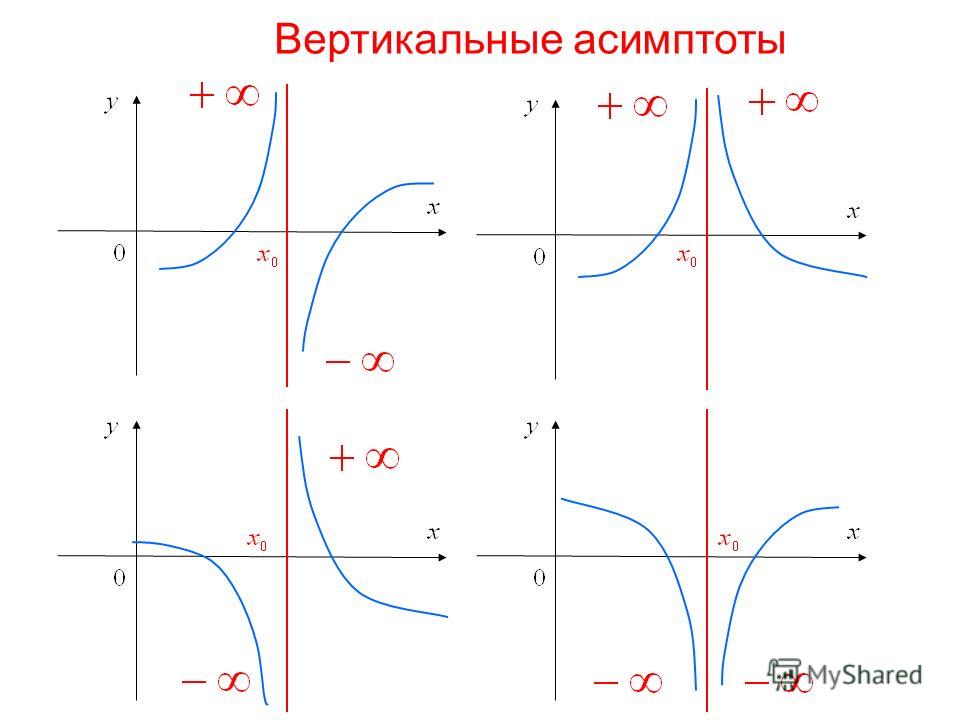

Не путайте вертикальные асимптоты с точками разрыва; асимптоты определяются через пределы, а разрывы могут иметь другие характеристики.

Вертикальные и горизонтальные асимптоты. Ответы
При исследовании функции на наличие вертикальных асимптот важно учитывать все возможные значения переменной, которые могут привести к бесконечному поведению функции.

Математический анализ, 15 урок, Ассимптоты


При анализе сложных функций с несколькими вертикальными асимптотами, разрабатывайте стратегии для изучения каждой из них отдельно, а затем совместно.

Асимптоты функции. Наклонная асимптота. 10 класс.

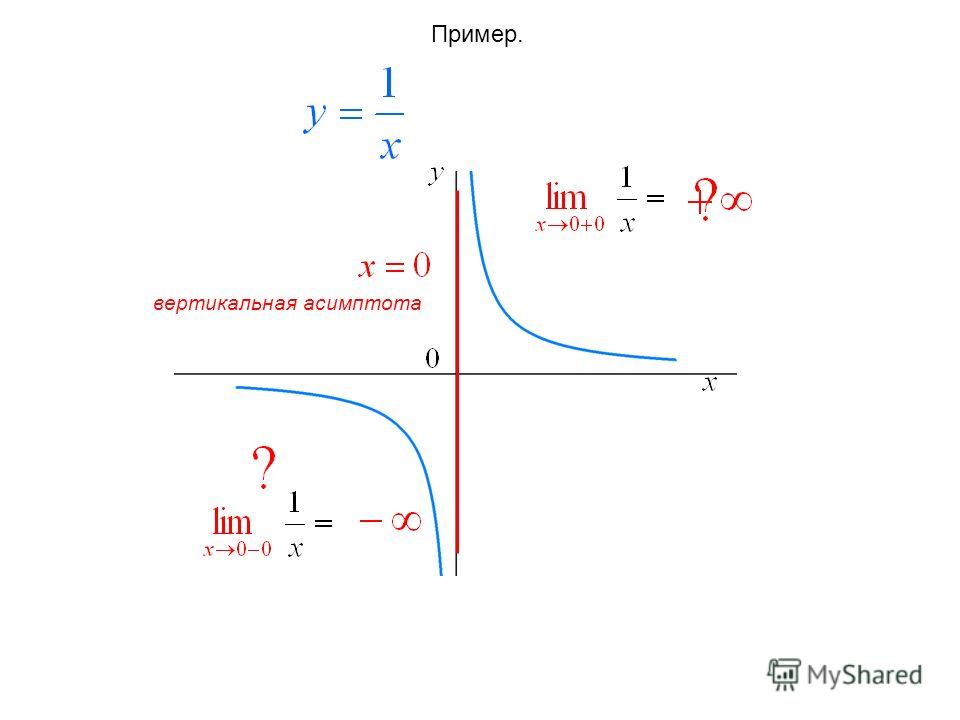
Используйте математические программы и графические калькуляторы для более точного и наглядного изучения вертикальных асимптот.

Пределы №6 Нахождение асимптот графиков функций
Сравните поведение функции с вертикальными асимптотами в различных точках и на различных интервалах, чтобы получить полное представление о её характеристиках.
Внимательно анализируйте случаи, когда вертикальные асимптоты могут не существовать, и функции могут быть определены для всех значений переменной.
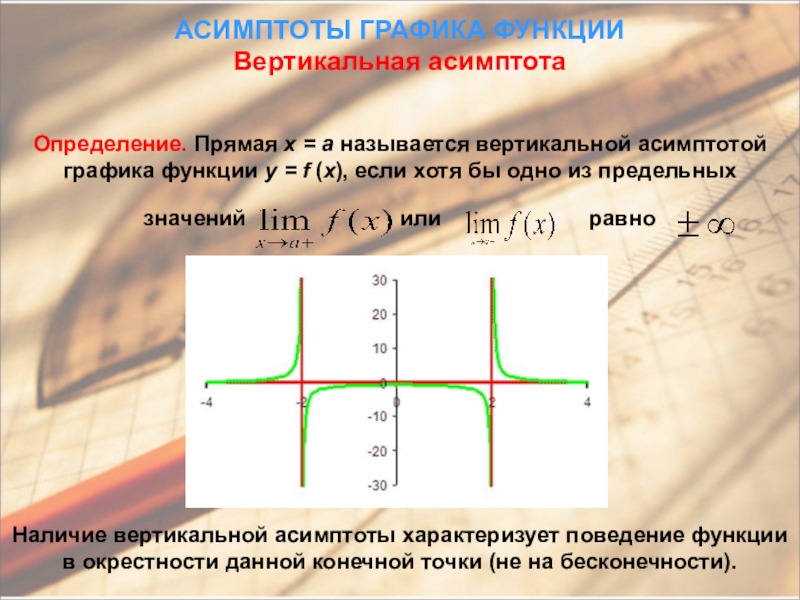

Рассматривайте вертикальные асимптоты как часть общего анализа функции и включайте их в более широкий контекст исследования функции и её графика.
