Методы вычисления алгебраического дополнения для a14
Алгебраическое дополнение элемента матрицы a14 — это важное понятие в линейной алгебре, которое помогает в вычислении определителей и решении систем линейных уравнений. В этом руководстве мы подробно рассмотрим, как правильно найти алгебраическое дополнение элемента матрицы, используя различные методы и примеры.


Определите главную матрицу и элемент, для которого нужно найти алгебраическое дополнение.

Нахождение определителя путём элементарных преобразований


Убедитесь, что вы правильно выбрали подматрицу, исключив соответствующую строку и столбец из исходной матрицы.

алгебра 8 класс номер 14
Рассчитайте детерминант подматрицы, полученной после удаления строки и столбца элемента a14.

Как найти алгебраическое дополнение?

Не забывайте учитывать знак алгебраического дополнения, который определяется по формуле (-1)^(i+j), где i и j — индексы строки и столбца элемента a14.
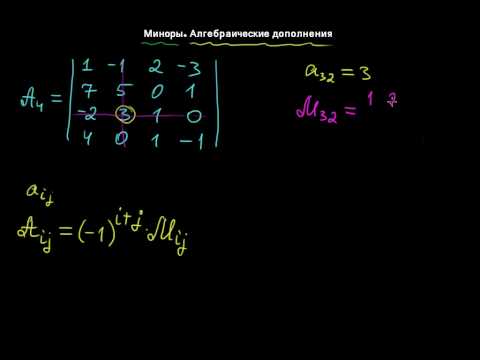
§12 Миноры. Алгебраические дополнения

Проверьте все вычисления на точность, особенно если работа с матрицами включает большие числа или сложные вычисления.
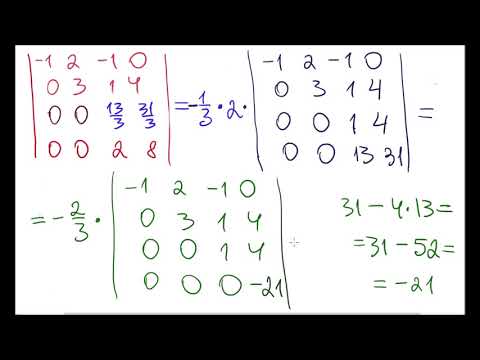
Вычислить определитель путём накопления нулей в строке или столбце

Используйте математические программы или калькуляторы для проверки своих результатов при сложных матрицах.

Видеоурок \
Просматривайте примеры решений и практикуйтесь на различных матрицах для лучшего понимания процесса.


Читайте учебные материалы и руководства по линейной алгебре для углубления своих знаний о вычислении алгебраических дополнений.

Линейная алгебра: матрицы, определители, метод Крамера. Высшая математика


Рассмотрите использование программного обеспечения для вычисления определителей и алгебраических дополнений для упрощения задач.


Консультируйтесь с преподавателями или экспертами по математике, если у вас возникли трудности в процессе вычисления.
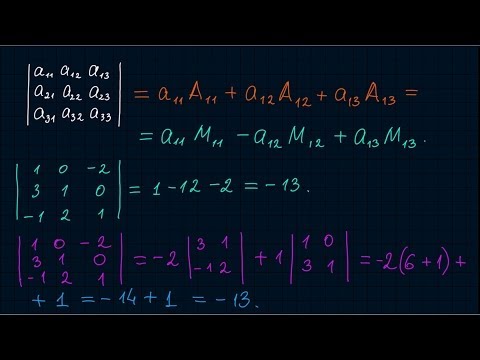
Миноры и алгебраические дополнения


Разбор задания №14. Поймет даже твой кот // ЕГЭ Информатик Родя