Основные формулы для комплексных чисел и их применение
В этой статье вы найдете подборку фотографий и полезные советы по трем важным формулам, которые помогут вам в работе с комплексными числами. Ознакомьтесь с формулами и рекомендациями для их использования.



Изучите формулу комплексного сопряжения, которая помогает находить комплексные числа, имеющие одинаковую действительную часть и противоположные мнимые части.

Формула Муавра. Возведение комплексного числа в степень

Помните, что модуль комплексного числа можно найти с помощью формулы: модуль равен квадратному корню из суммы квадратов действительной и мнимой частей.

Тригонометрическая форма комплексного числа
Используйте формулу для умножения комплексных чисел: произведение равно произведению их модулей и сумме их аргументов.

Комплексные числа. Тригонометрическая форма. Формула Муавра - Ботай со мной #040 - Борис Трушин !

При работе с делением комплексных чисел, не забудьте про формулу деления: деление равно отношению их модулей и разности их аргументов.

Математика без Ху%!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.

Для нахождения аргумента комплексного числа используйте арктангенс отношения мнимой части к действительной части.
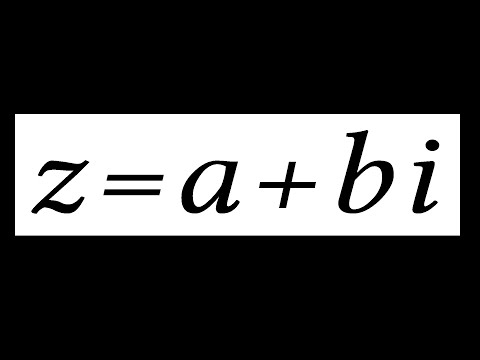
КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТ

Помните, что при возведении комплексного числа в степень, необходимо использовать формулу Муавра.

При работе с комплексными числами в тригонометрической форме, используйте формулу Эйлера.

10 класс, 34 урок, Тригонометрическая форма записи комплексного числа

Для нахождения обратного комплексного числа используйте формулу, где делитель равен сумме квадратов действительной и мнимой частей.

Комплексный анализ, Лекция 3, artimpression.ruпка

Изучите применение формул для перехода между алгебраической и тригонометрической формами комплексных чисел.

3. Тригонометрическая форма комплексного числа

Не забывайте проверять результаты своих вычислений, особенно при работе с мнимыми частями.

10 класс, 32 урок, Комплексные числа и арифметические операции над ними


4. Показательная форма комплексного числа