Эластичность функции в точке х0: ключевые моменты и советы
Эластичность функции в точке х0 - это важный математический концепт, помогающий определить, как функция реагирует на изменения переменных. В этом руководстве мы рассмотрим основные аспекты и предложим полезные советы для лучшего понимания.

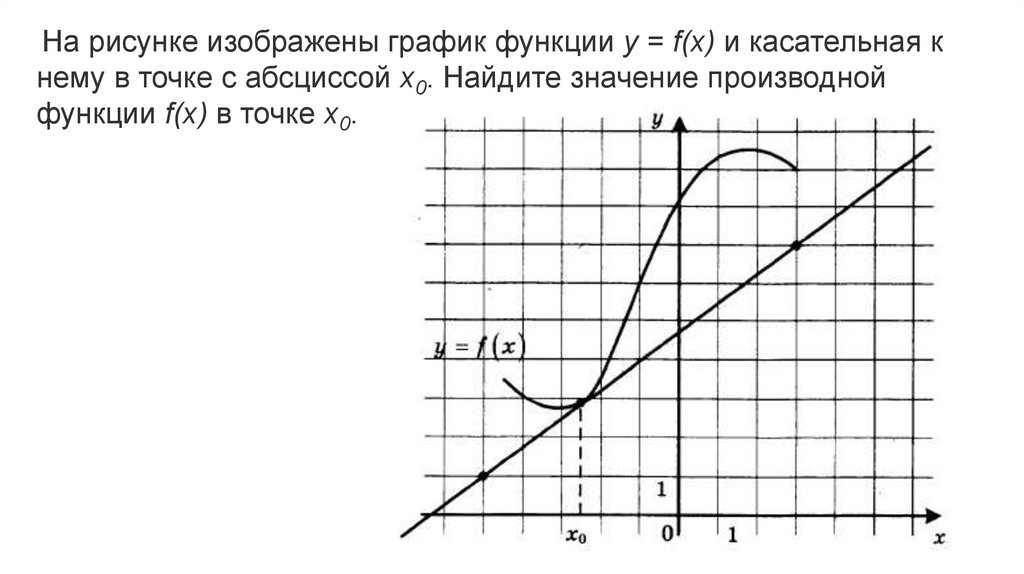

Понимание определения: эластичность функции в точке х0 описывает, насколько сильно изменяется значение функции при небольшом изменении переменной.

3.4 Эластичность

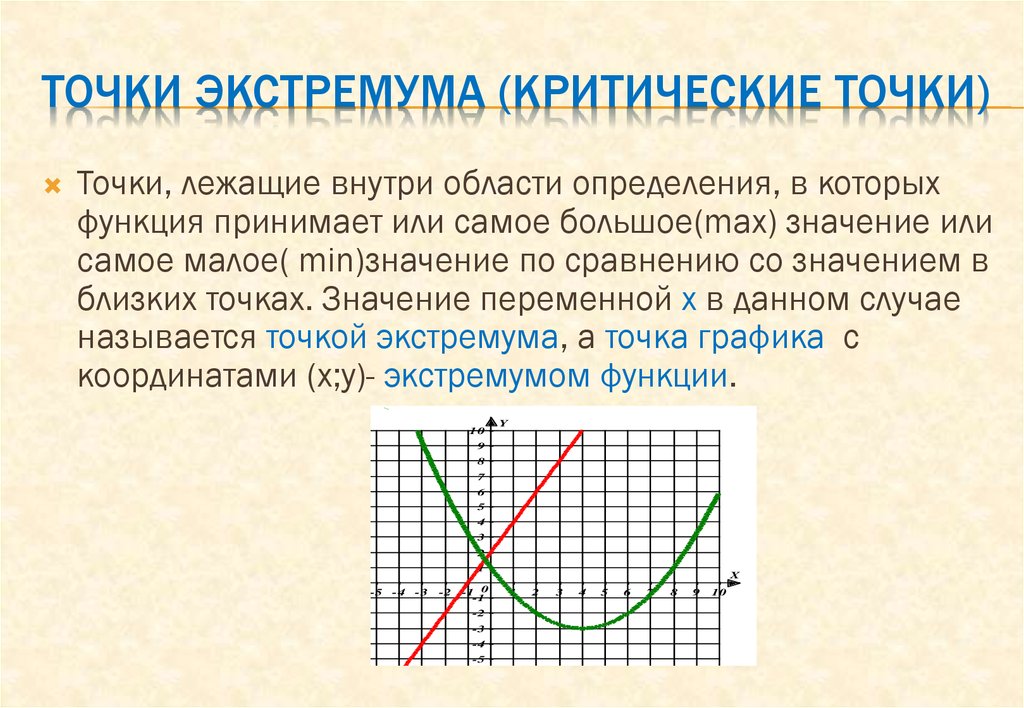
Изучите график: визуализация функции может помочь лучше понять, как она изменяется в точке х0.
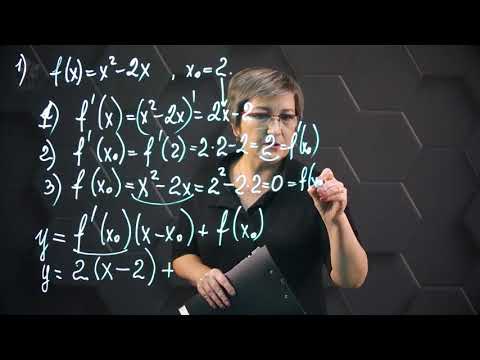
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.

Используйте производную: первая производная функции в точке х0 дает представление о скорости изменения функции.

Эластичность спроса и предложения - Как цена влияет на спрос

Практикуйтесь с примерами: решайте задачи с разными функциями, чтобы лучше усвоить концепт эластичности.

3.2.3. Линейный и постоянно эластичный спрос
Обратите внимание на единицы измерения: понимание единиц измерения поможет в интерпретации результатов.
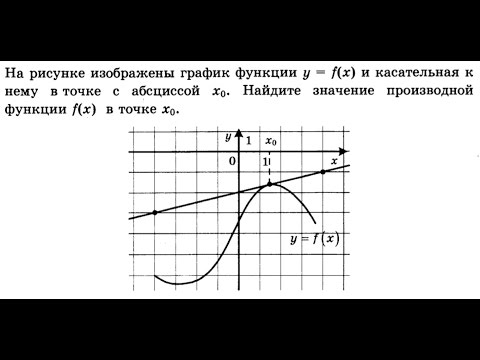
ЕГЭ 2017 Профильный №7 найти производную в точке касания #7
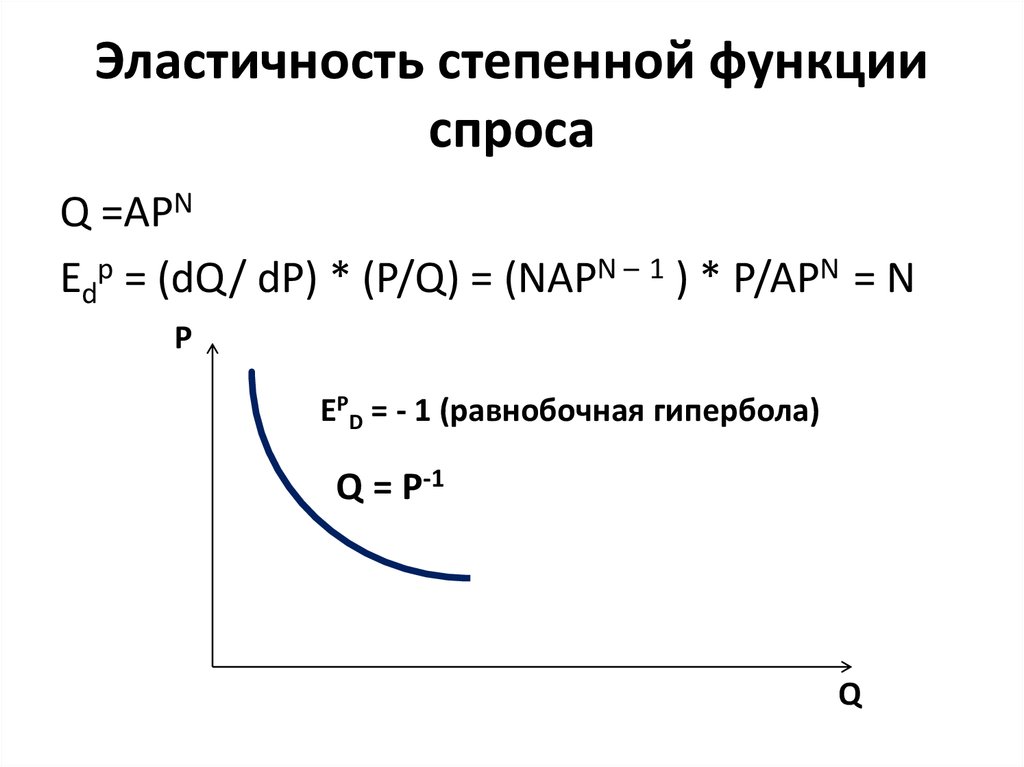
Ищите симметрию: симметричные функции могут облегчить понимание изменений в точке х0.
Используйте онлайн-ресурсы: видеоуроки и статьи могут предоставить дополнительные объяснения и примеры.


Проверьте граничные случаи: исследование поведения функции на границах может дать дополнительные инсайты.

Предел функции в точке. 10 класс.
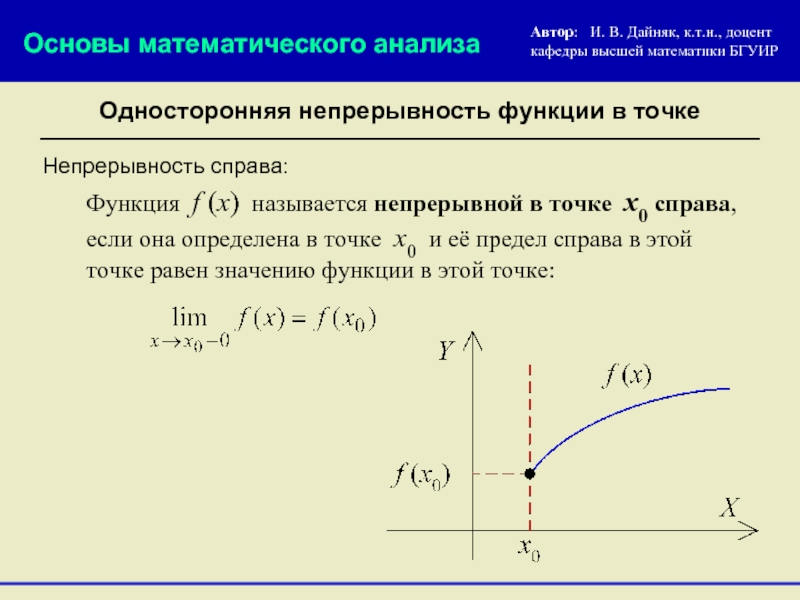
Консультируйтесь с преподавателями: если что-то не понятно, обращайтесь за помощью к экспертам.
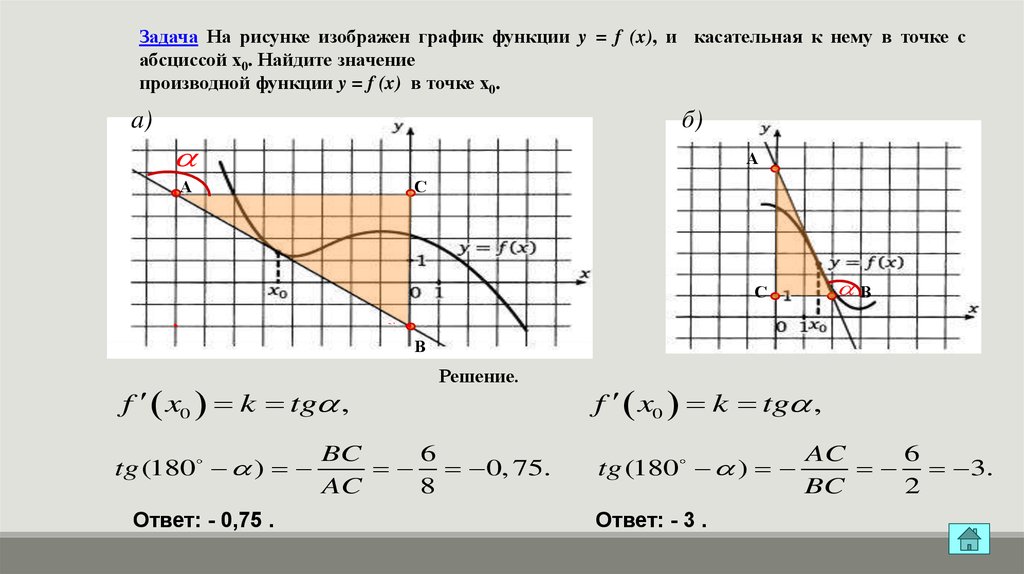
Закрепляйте теорию на практике: применяйте полученные знания в реальных задачах, чтобы лучше их усвоить.

Производная в точке. Алгебра 10 и 11 класс.