Комбинаторика: основные элементы и их применение

Комбинаторика – раздел математики, изучающий способы выбора и расположения элементов. В данной статье рассмотрены перестановки, размещения и сочетания, их свойства и примеры применения.

Перестановки используются для определения количества способов, которыми можно расположить все элементы множества в определенном порядке.

Размещения позволяют определить количество способов выбора и расположения части элементов множества в определенном порядке.

Сочетания определяют количество способов выбора элементов из множества без учета порядка.

Формула для перестановок: n! (факториал числа n).

Формула для размещений: A(n, k) = n! / (n - k)!, где n – общее число элементов, k – количество выбираемых элементов.

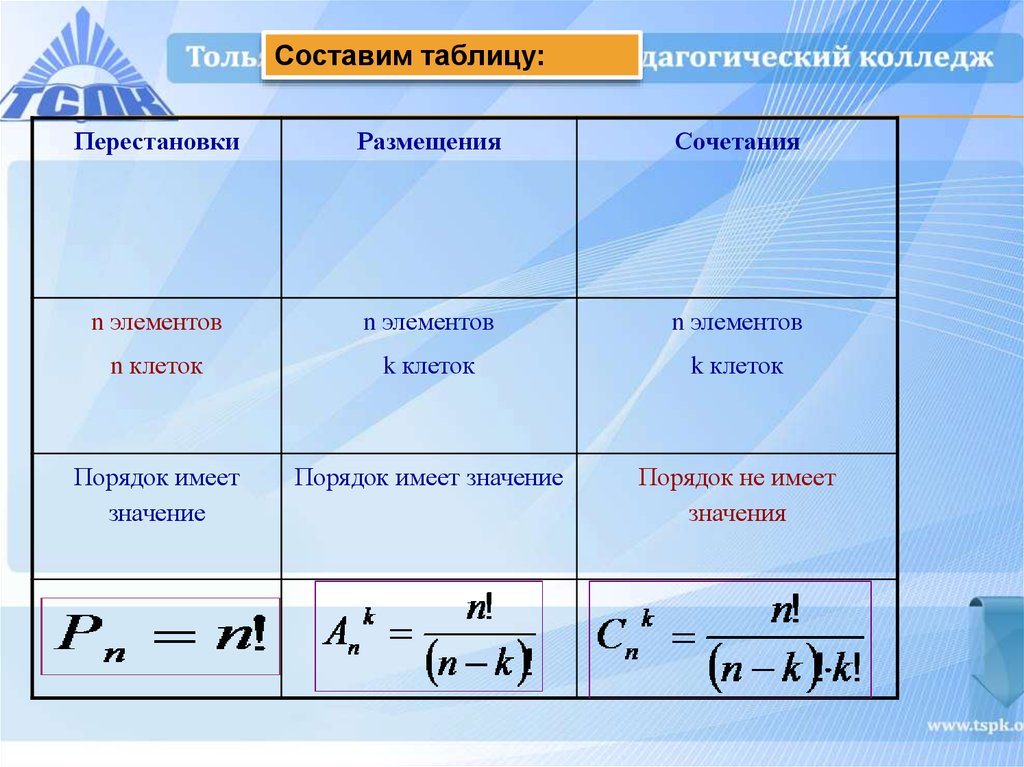
Формула для сочетаний: C(n, k) = n! / (k!(n - k)!), где n – общее число элементов, k – количество выбираемых элементов.

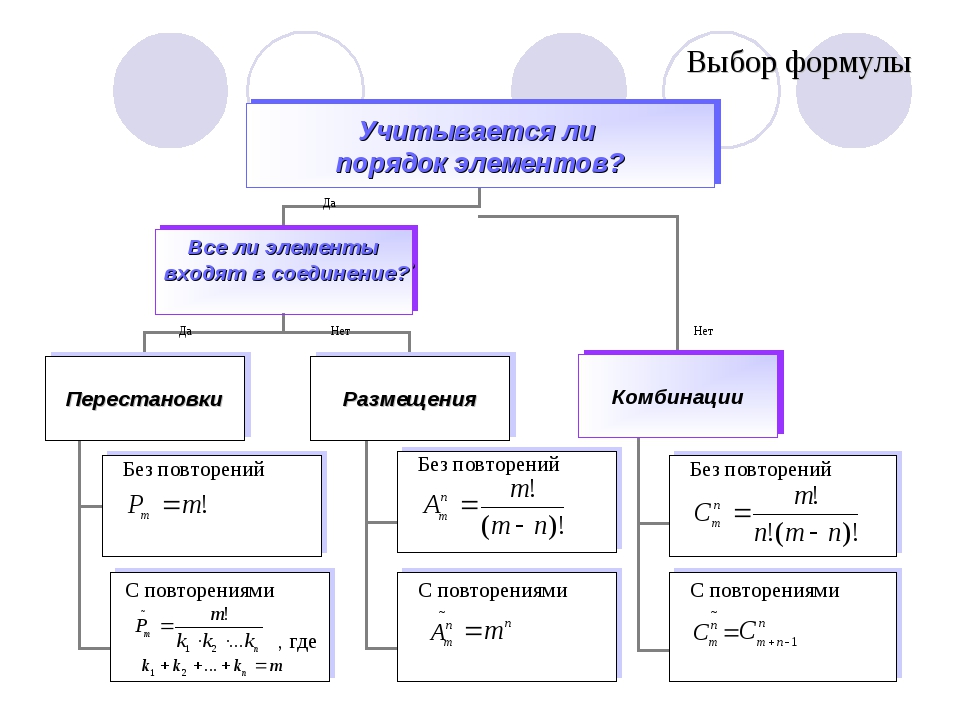
Используйте перестановки при решении задач, связанных с порядком, например, в организации событий или размещении предметов.

Размещения полезны для задач, где важен не только выбор, но и порядок элементов, таких как составление списков или планов.

Сочетания подходят для задач, где порядок не имеет значения, например, при выборе подмножества из множества объектов.

Запоминайте основные формулы и их применение через практику, решая задачи различной сложности.