Как проверить функцию на дифференцируемость: полное руководство
На этой странице вы найдете полезные советы и фотографии, которые помогут вам научиться исследовать функции на дифференцируемость. Подробные инструкции и наглядные примеры облегчат понимание этого важного математического аспекта.



Начните с проверки непрерывности функции, так как дифференцируемость предполагает непрерывность.

Подготовка к экзаменам: дифференцируемость функций, производные, исследование функций
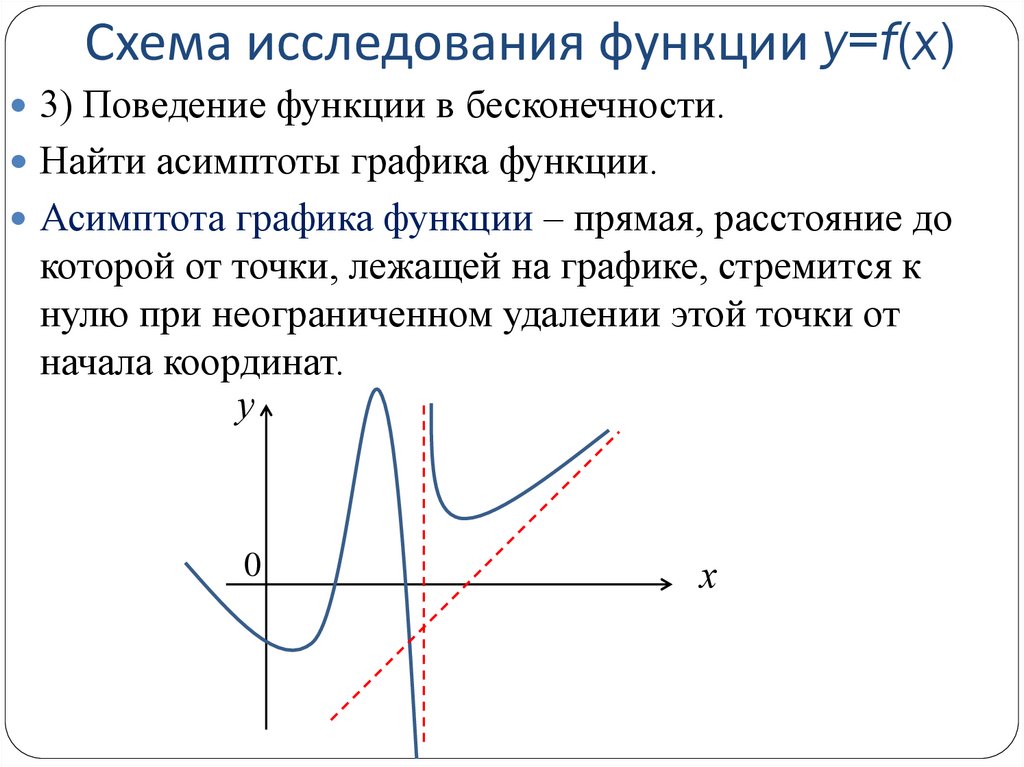

Определите область определения функции и проверьте её на разрывы.

Исследование дифференцируемости.
Рассчитайте производную функции в различных точках, чтобы проверить её существование.

Матан. Дифференцируемость функций многих переменных. Разбор задач на функции многих переменных.


Используйте правило Лопиталя для проверки пределов при исследовании дифференцируемости.

Исследование функции на дифференцируемость (часть 1)

Проверьте производные на краевых точках области определения функции.

✓ Дифференцируемая функция. Дифференциал - матан #032 - Борис Трушин


Используйте графическое представление функции для визуальной оценки её дифференцируемости.

Изучите вторую производную функции, чтобы получить больше информации о её поведении.

Исследование функции на дифференцируемость (часть 2)

Применяйте различные методы нахождения производных для проверки их совпадения.
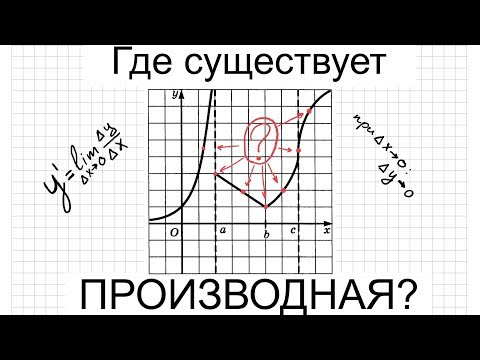
Производная. Часть 5. Дифференцируемость и непрерывность функции. Несуществование производной.


Обратите внимание на возможные точки перегиба, которые могут указывать на изменение дифференцируемости.

Дифференцируемость в точке решение примеров

Используйте примеры и задачи из учебников для практики и проверки своих знаний.

Непрервность и дифференцируемость ФМП разбор контрольной
Математика без Ху%!ни. Исследование функции, график. Первая, вторая производная, асимптоты.