Коэффициент корреляции: Инструменты, примеры и полезные советы
Коэффициент корреляции является важным статистическим инструментом для измерения степени взаимосвязи между двумя переменными. В этой подборке вы найдете полезные советы и примеры, которые помогут лучше понять и использовать этот коэффициент в различных исследованиях и анализах данных.



Определите тип данных, с которыми вы работаете, чтобы выбрать правильный метод расчета коэффициента корреляции.

Коэффициент корреляции Пирсона


Используйте графическое представление данных, такое как диаграммы рассеяния, чтобы визуально оценить наличие корреляции.
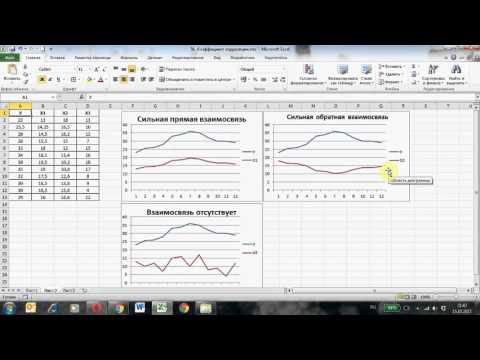
Расчет коэффициента корреляции в Excel
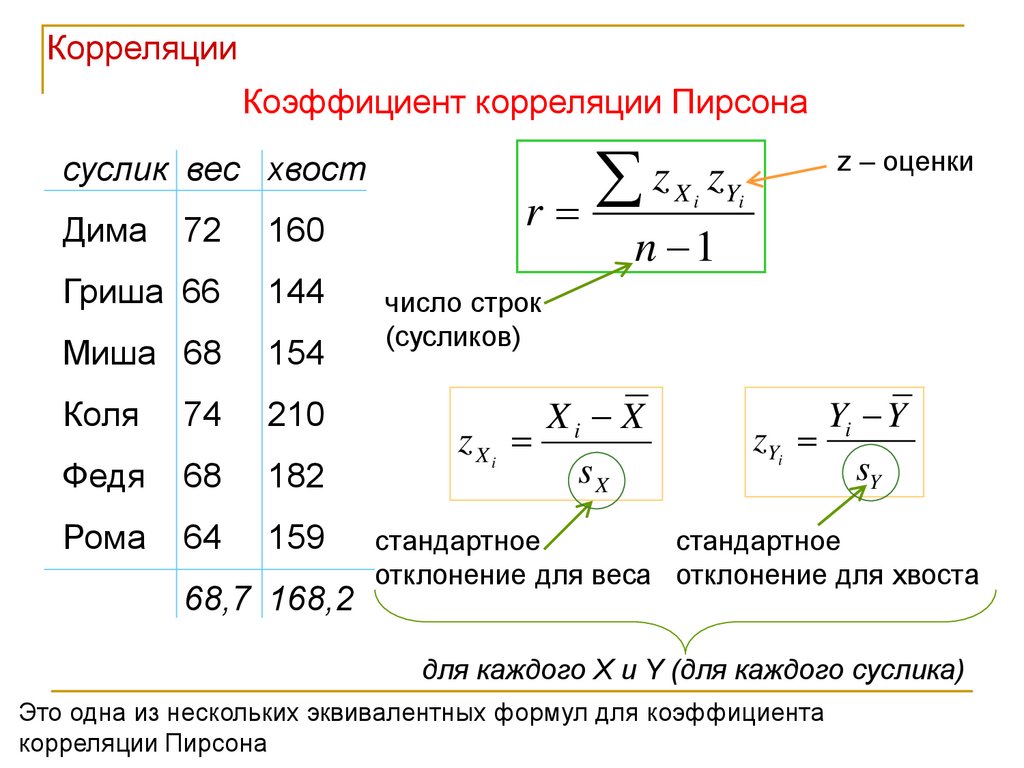
Помните, что корреляция не означает причинно-следственную связь. Высокий коэффициент корреляции не доказывает, что одна переменная вызывает изменения в другой.
Коэффициент корреляции Пирсона в Excel


Используйте программные инструменты, такие как Excel или специализированные статистические пакеты, для точного расчета коэффициента корреляции.

Коэффициент корреляции Пирсона


Проверяйте наличие выбросов в данных, так как они могут существенно влиять на значение коэффициента корреляции.

Huawei Watch GT 5 и Watch GT 5 Pro научный обзор


Учтите, что коэффициент корреляции имеет значение от -1 до 1, где -1 указывает на идеальную отрицательную корреляцию, 1 — на идеальную положительную, а 0 — на отсутствие корреляции.
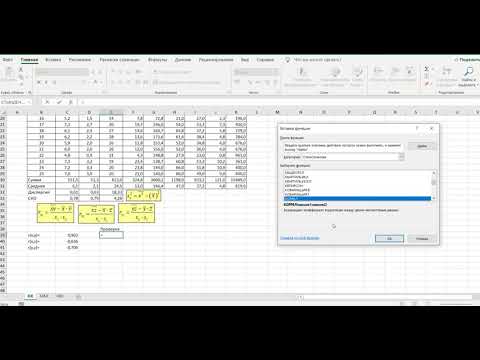
Коэффициент корреляции. Статистическая значимость
Используйте метод Пирсона для расчета линейной корреляции между двумя количественными переменными.
Для не параметрических данных или рангов используйте коэффициент Спирмена.

Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величин


При интерпретации коэффициента корреляции учитывайте контекст исследования и предметную область.

Коэффициент корреляции - Борис Миркин

Обязательно проверяйте статистическую значимость полученного коэффициента корреляции, чтобы убедиться в его надежности.
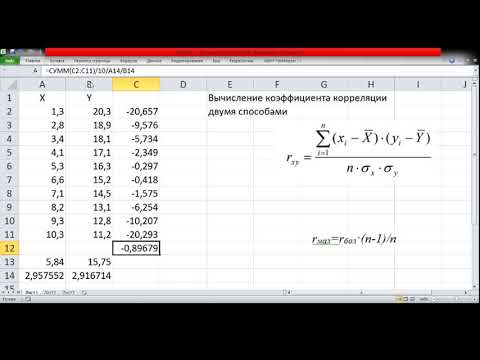
Коэффициент корреляции Пирсона, 2 способа вычисления
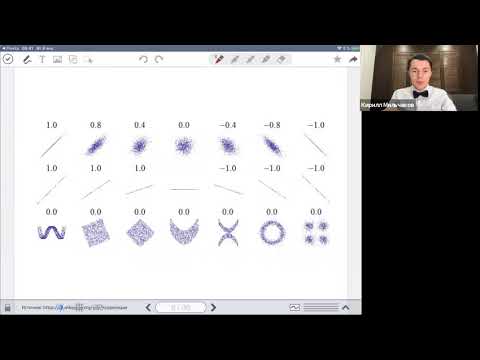
Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессия