Медиана треугольника: полное руководство по определению и свойствам
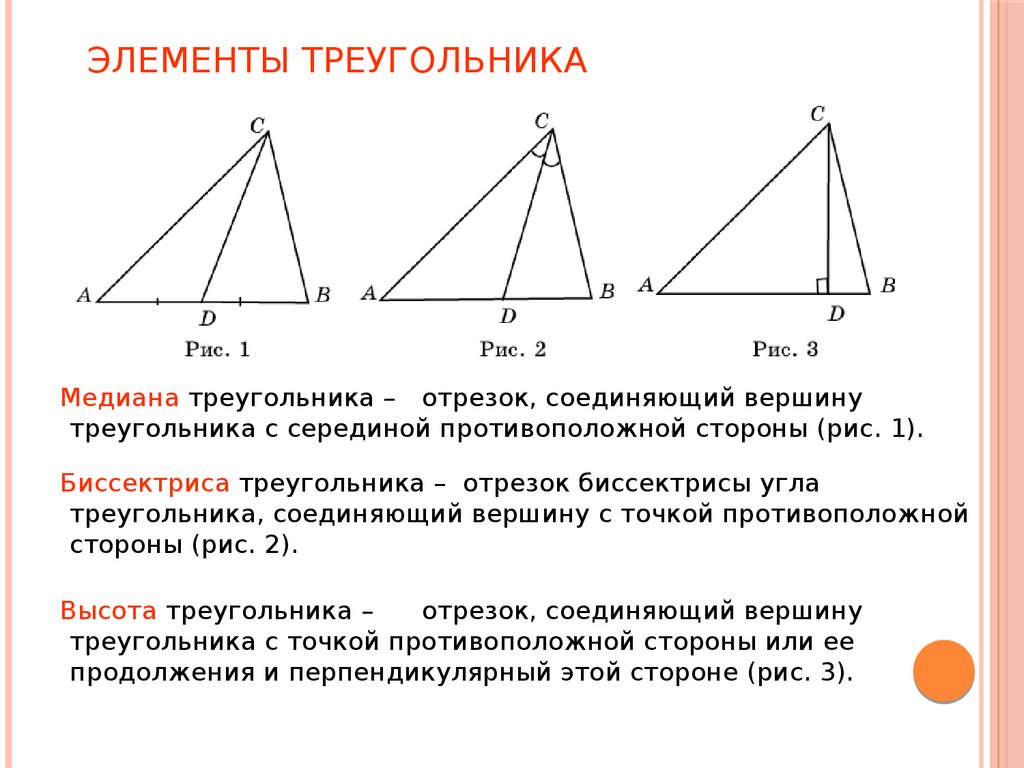
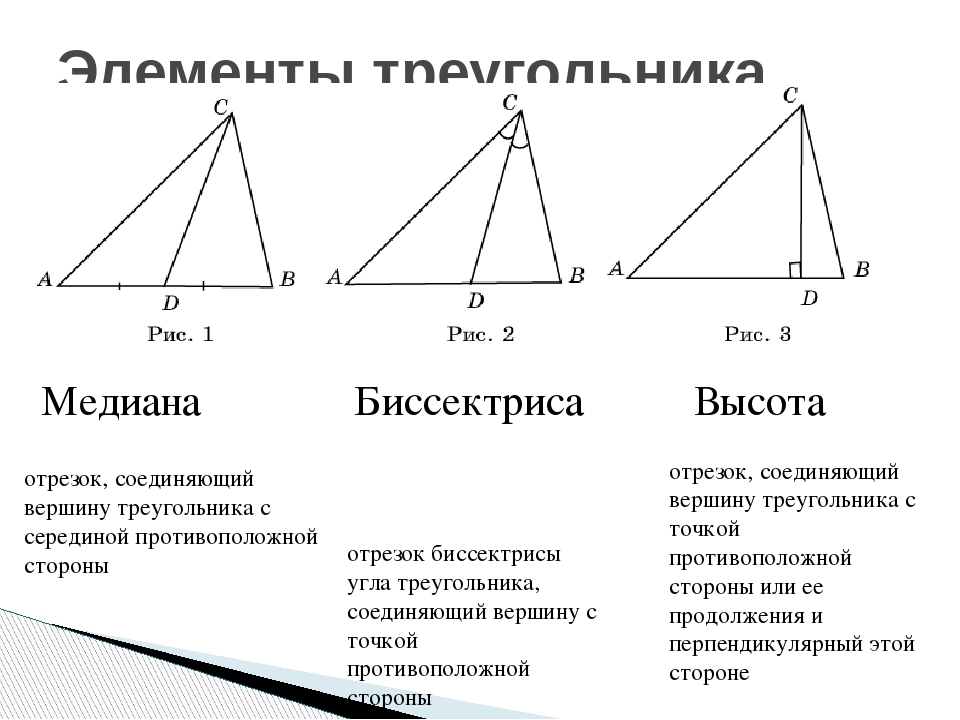
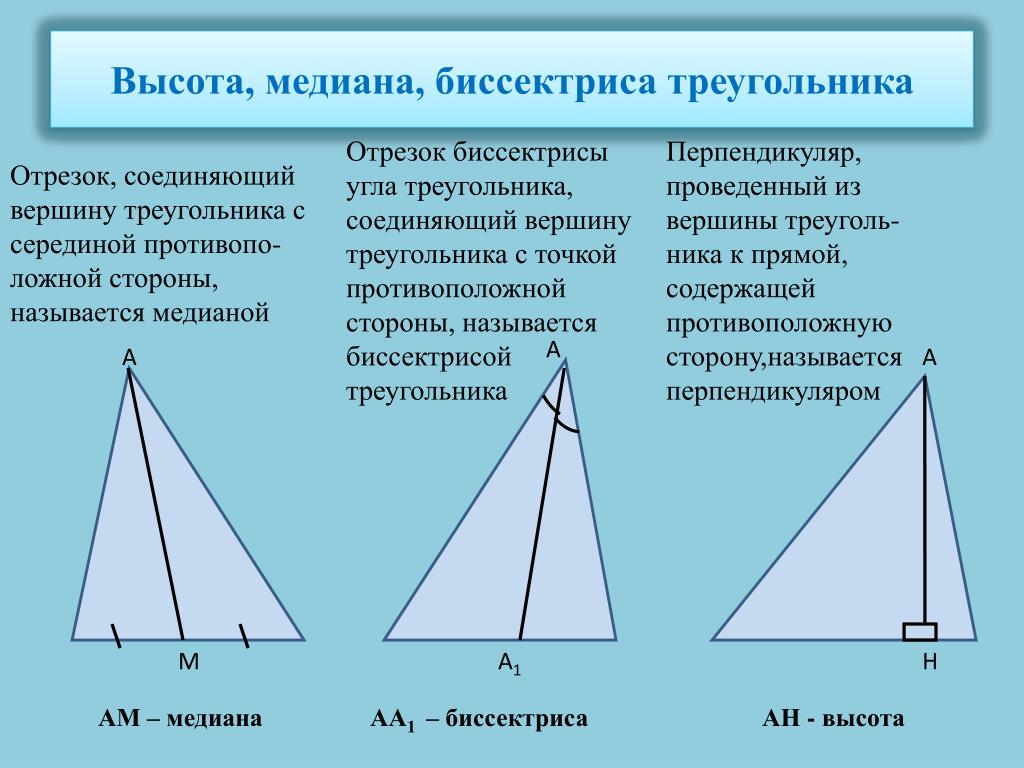
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Важно понимать ее свойства и применение для решения различных геометрических задач.


Медиана всегда делит противоположную сторону на две равные части.
Медиана это обезьяна
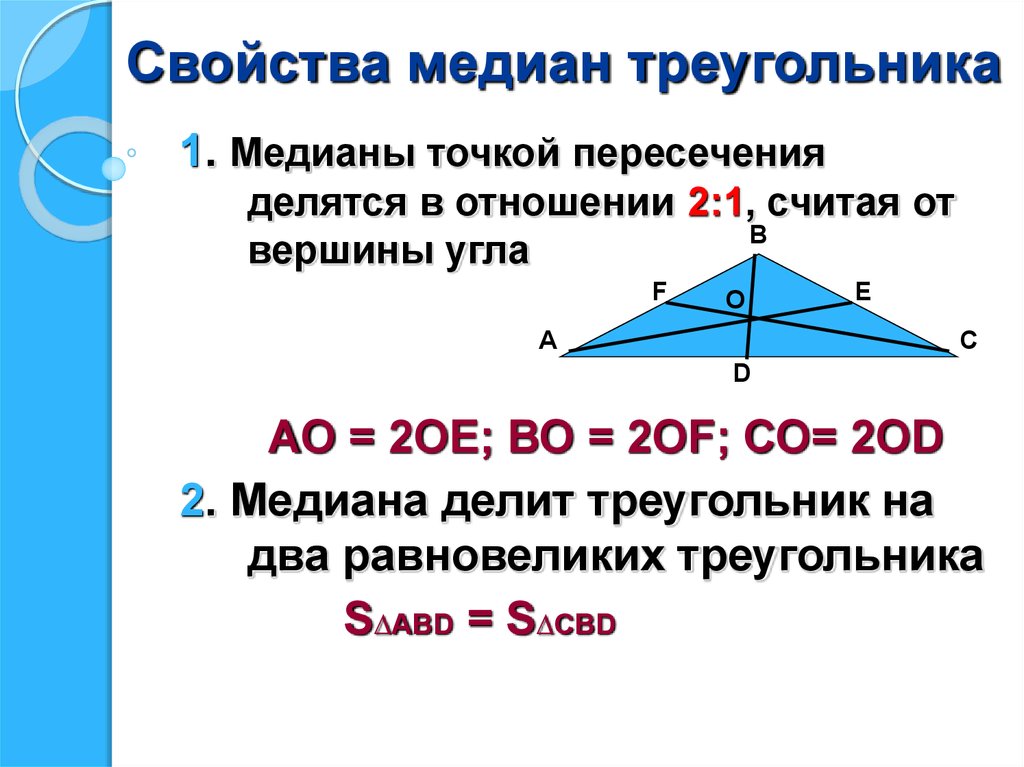
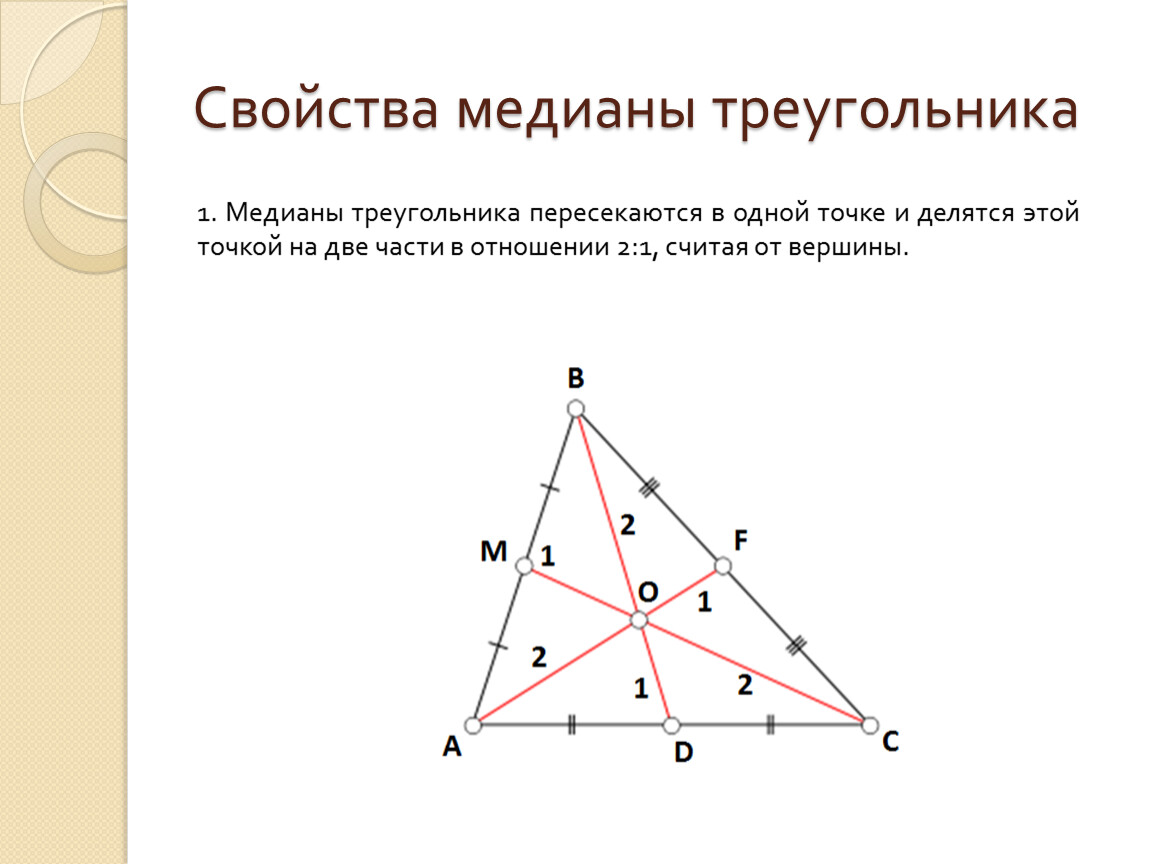
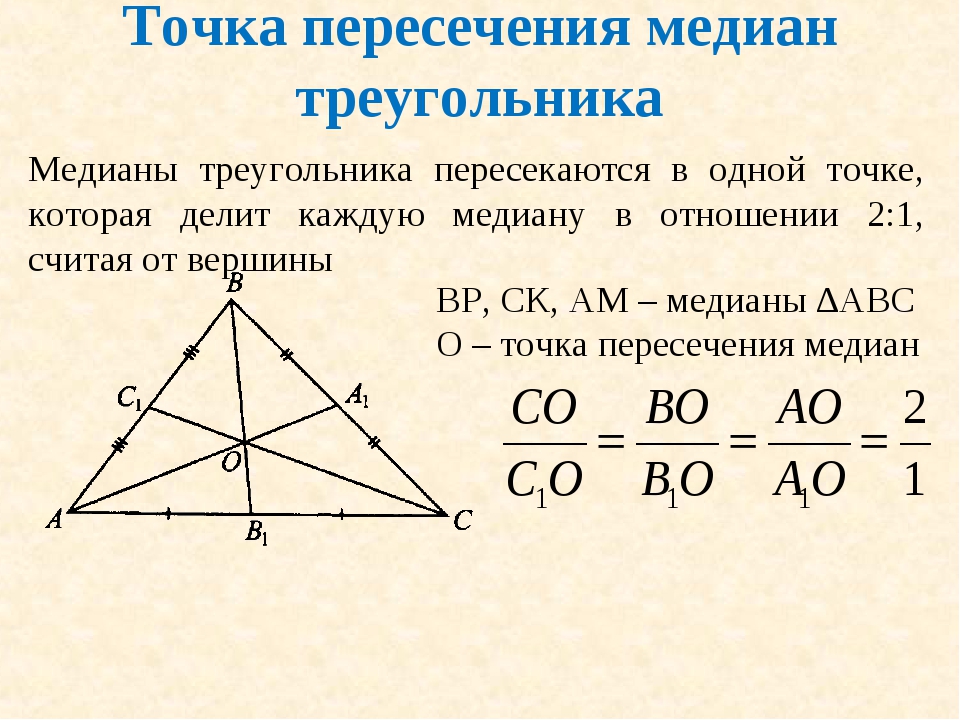
Точка пересечения медиан треугольника называется центроидом и делит каждую медиану в отношении 2:1, считая от вершины.

Геометрия 7. Треугольники. Медиана и биссектриса треугольника. Определение и свойства. Решение задач
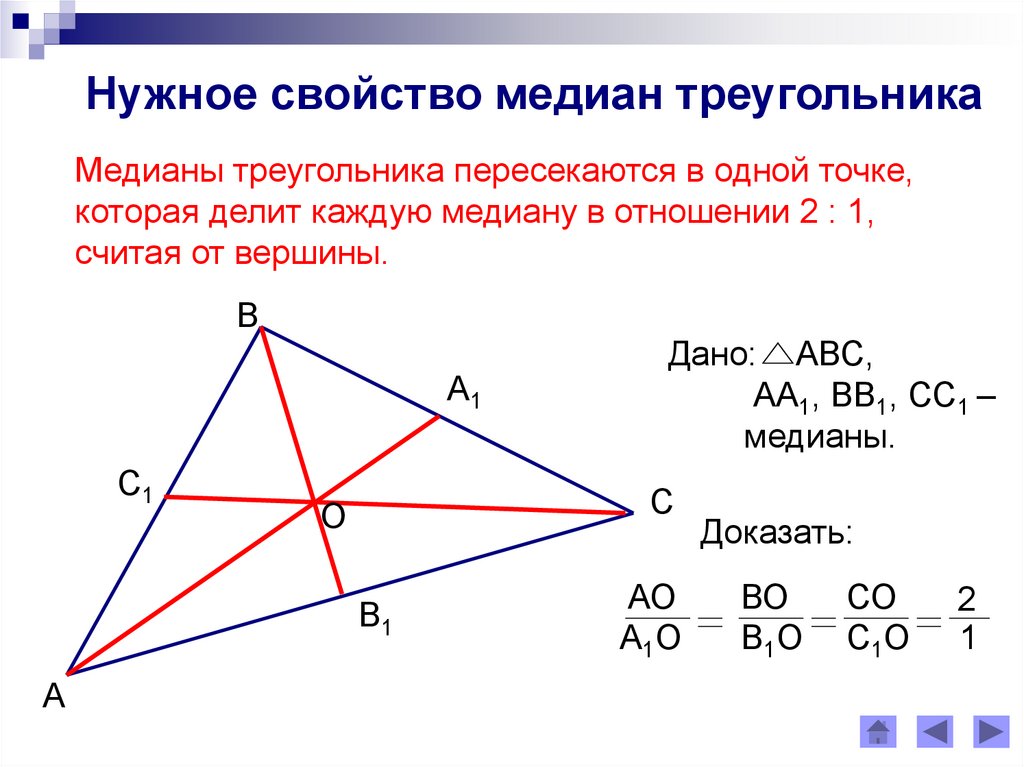
Во всех типах треугольников медиана обладает одинаковыми свойствами.

Медиана как статистическая характеристика
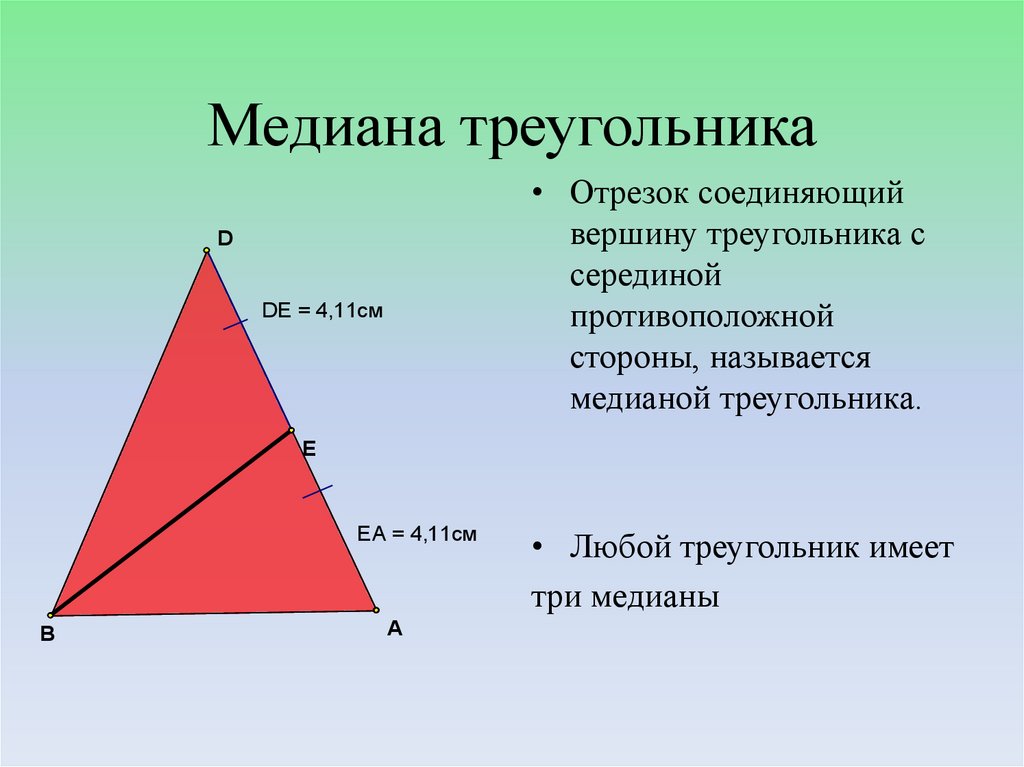
Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.

Медиана треугольника. Построение. Свойства.
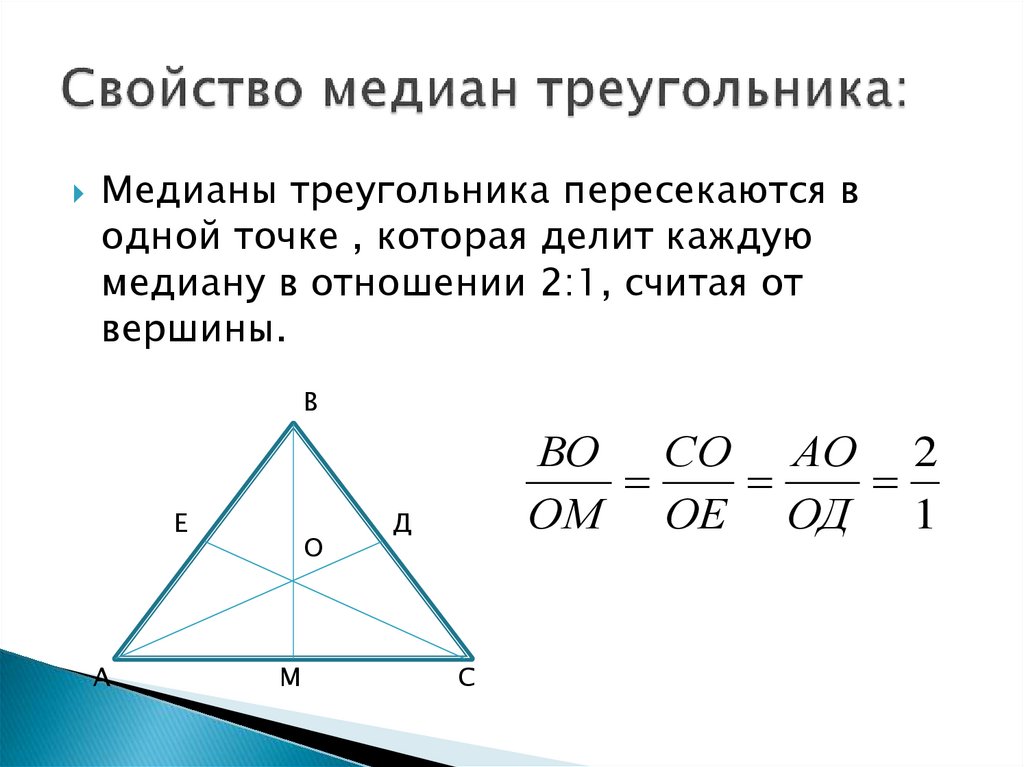
Для вычисления длины медианы можно использовать формулу: m=2b2+2c2−a2/2m = /sqrt{2b^2 + 2c^2 - a^2} / 2m=2b2+2c2−a2/2, где a, b, c - стороны треугольника.

ГЕОМЕТРИЯ 8 класс. Свойство медиан треугольника
В равностороннем треугольнике медианы также являются высотами и биссектрисами.
Высота, биссектриса, медиана. 7 класс.
Центроид делит медиану в соотношении 2:1 от вершины треугольника до середины противоположной стороны.

8. Медиана треугольника и её свойства.

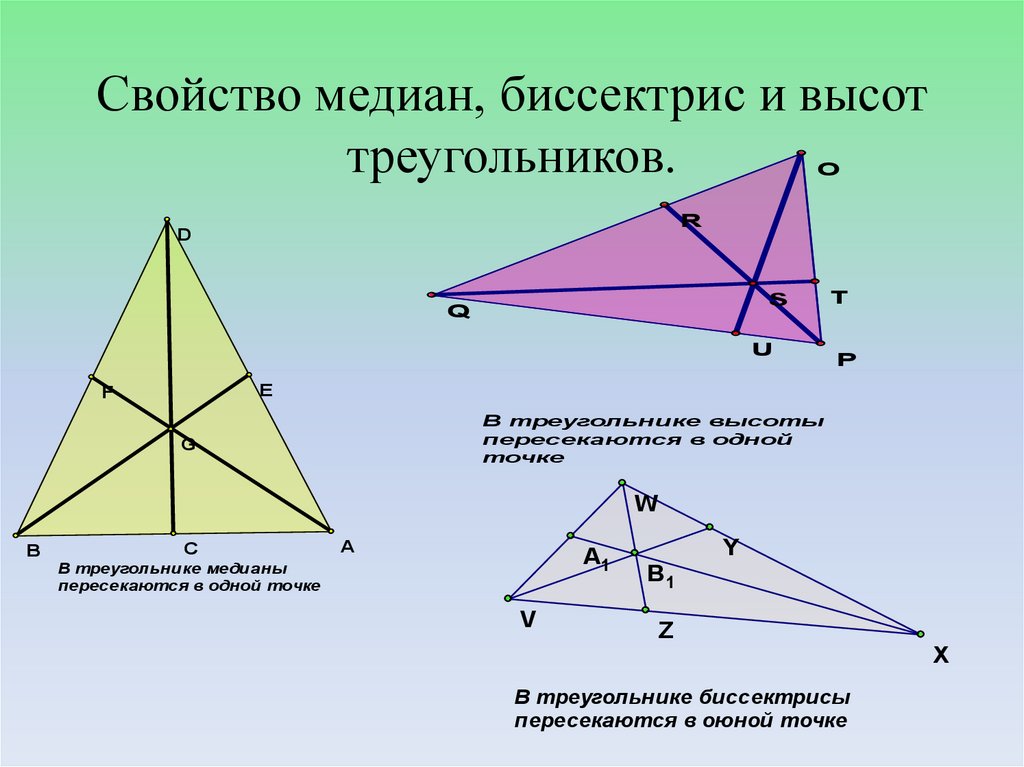
Медианы треугольника всегда пересекаются в одной точке, называемой центроидом.

Медиана треугольника и её свойства.

Формулы для медианы треугольника
Медианы можно использовать для построения срединного треугольника, у которого стороны равны половинам медиан исходного треугольника.
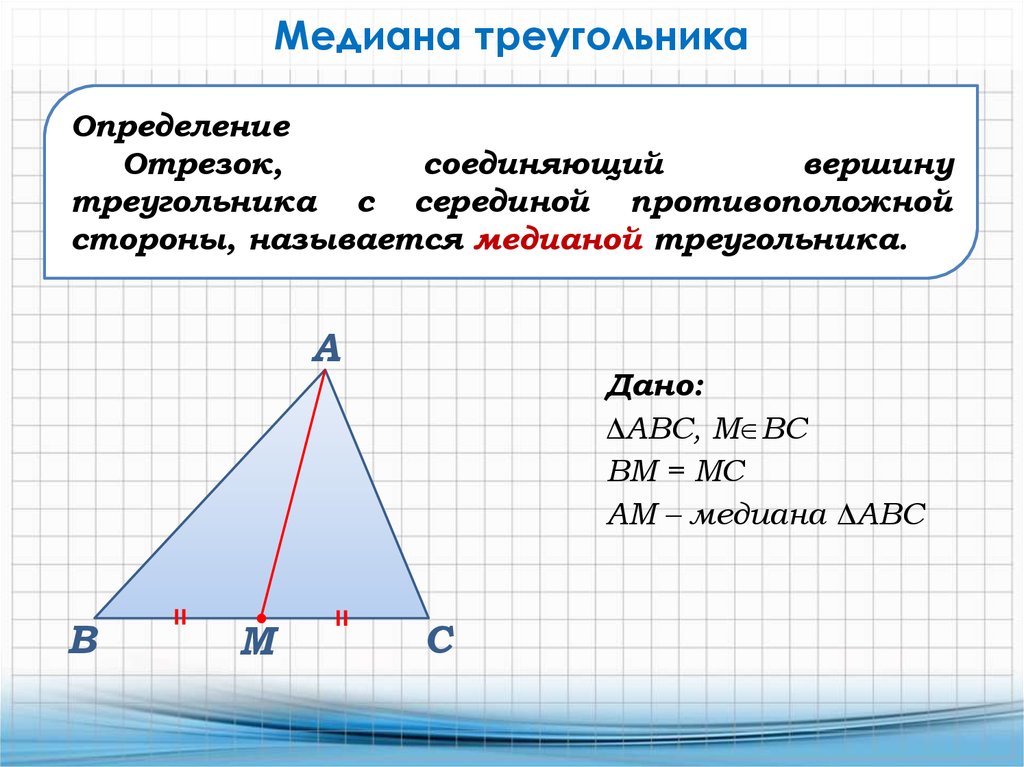
Понимание свойств медианы помогает в решении задач на нахождение площадей и центров масс треугольников.
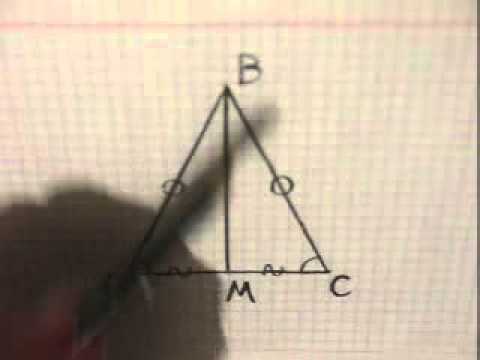
Теорема о свойстве медианы равнобедренного треугольника