Современные подходы к решению систем линейных уравнений
На этой странице вы найдете подборку фотографий и полезные советы по решению систем линейных алгебраических уравнений. Мы рассмотрим различные методы и подходы, которые помогут вам более эффективно решать задачи данного типа.



Начните с приведения системы к упрощенной форме, используя элементарные преобразования строк.
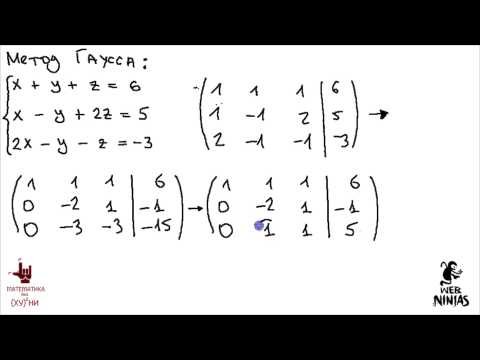
Математика без Ху%!ни. Метод Гаусса.

Используйте метод Гаусса для решения систем с любым количеством уравнений и неизвестных.

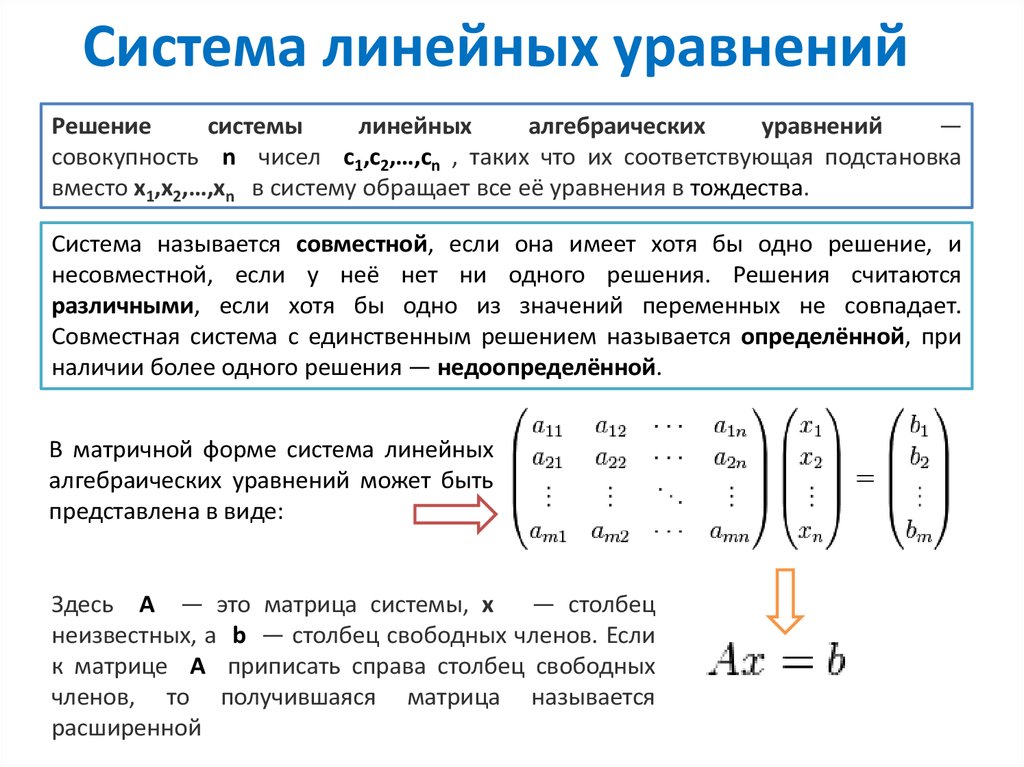
Линейная алгебра, Матрицы: Метод Гаусса. Высшая математика
При больших системах применяйте итерационные методы, такие как метод Якоби или метод Зейделя.

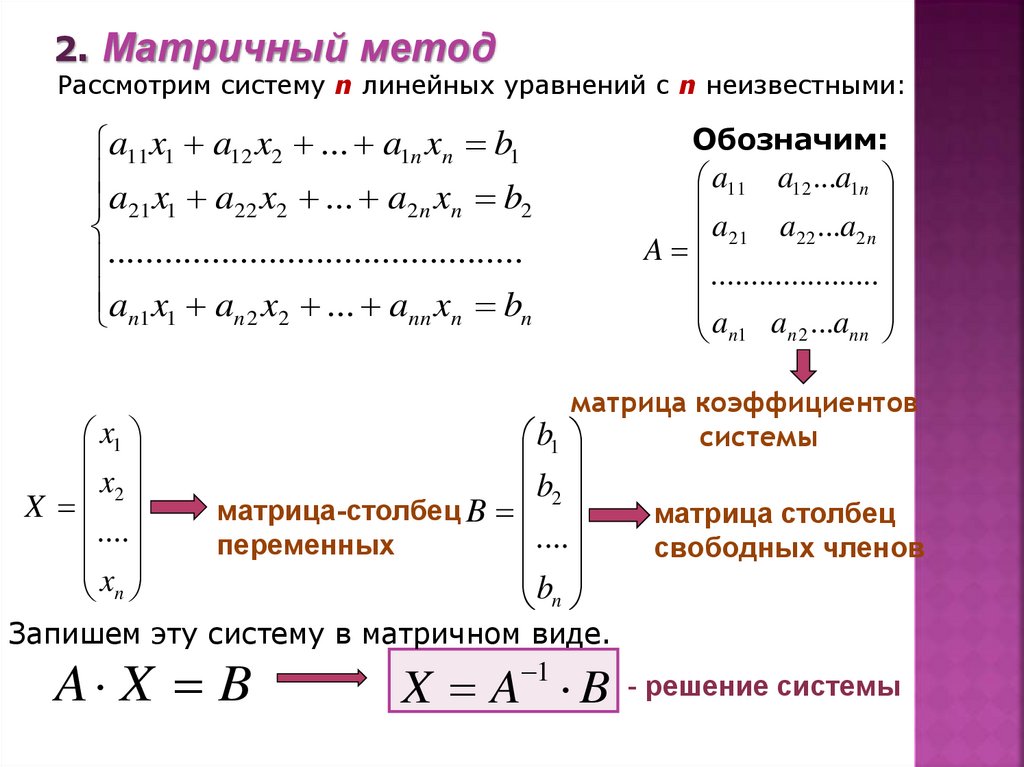
Решение системы уравнений методом обратной матрицы.

Регулярно проверяйте результаты на ошибки, особенно при ручных вычислениях.

Решение системы уравнений методом Гаусса

Используйте программное обеспечение, такое как MATLAB или Python, для автоматизации расчетов.

Эту задачу могут решить лишь единицы

Ознакомьтесь с методами факторизации матриц, такими как LU-разложение.
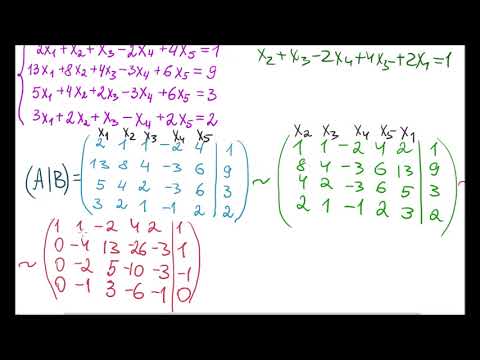
Система линейных уравнений. Общее решение. Метод Гаусса
При работе с плотными матрицами учитывайте возможность их разреженности для оптимизации вычислений.

Матричный метод решения систем уравнений

Не забывайте о проверке условий совместности системы, особенно для переопределенных систем.
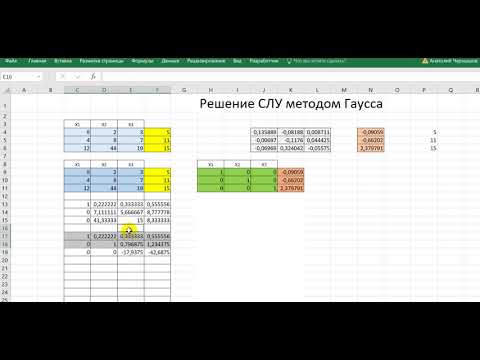
СЛУ Метод Гаусса в Excel
Изучайте и используйте теорию линейной алгебры, чтобы лучше понимать структуру и свойства систем уравнений.
Постоянно практикуйтесь в решении различных типов систем для повышения своего мастерства и уверенности.