Окружность, вписанная в треугольник: теория и практика
Эта страница посвящена методам вписывания окружности в треугольник и проведению касательных к ней. Вы найдете подробные инструкции и советы, которые помогут вам понять и применить эти геометрические концепции.
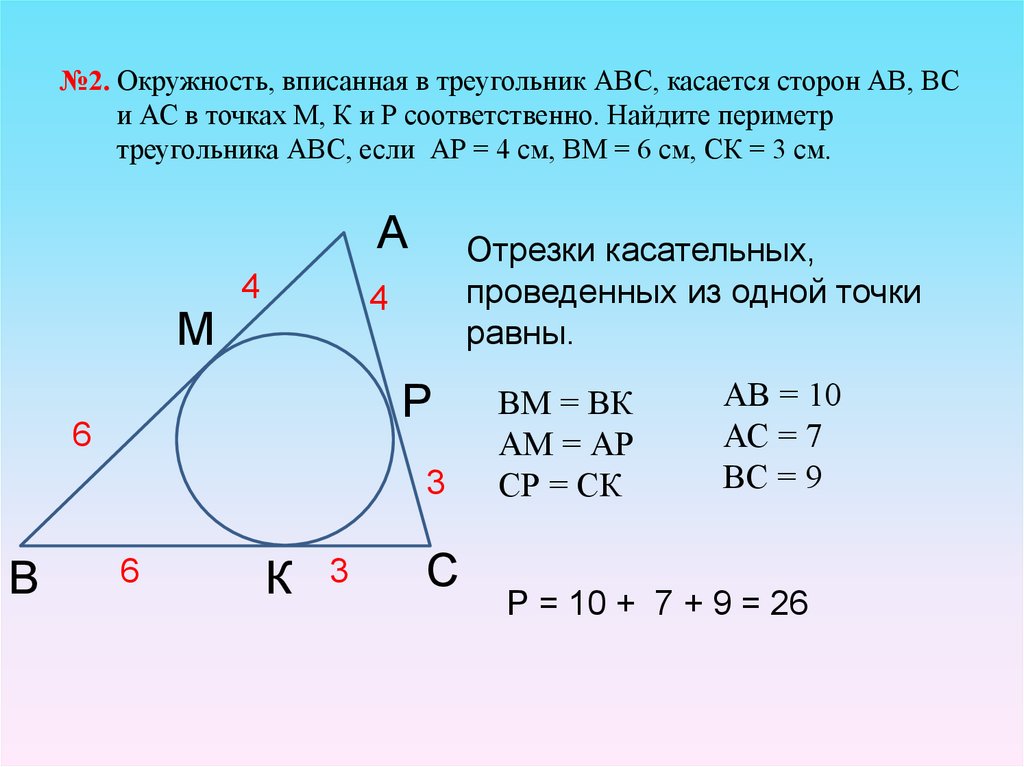
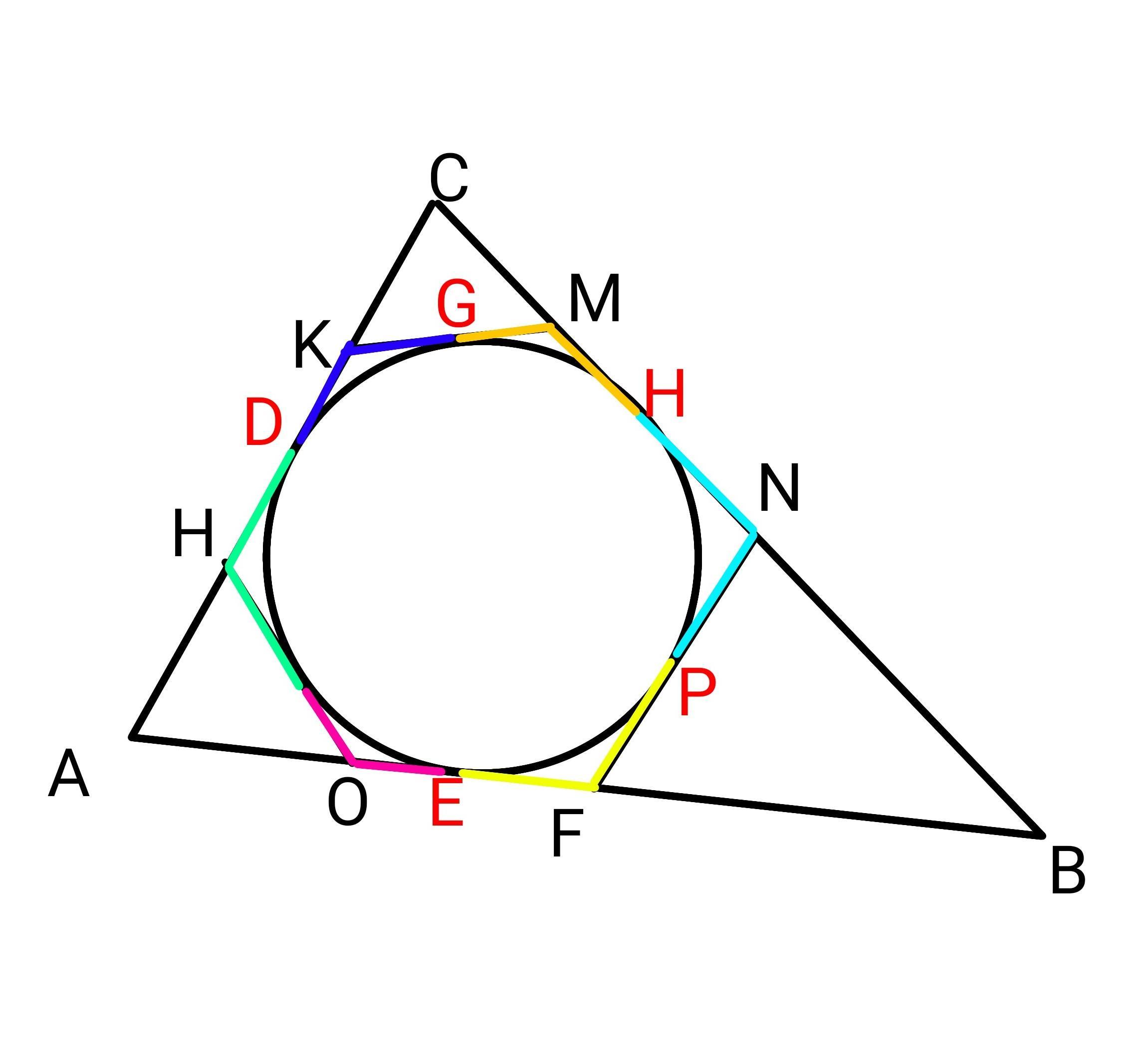
Для вписывания окружности в треугольник, необходимо найти точки пересечения биссектрис.

Вписанная и описанная окружности - Лайфхак для запоминания
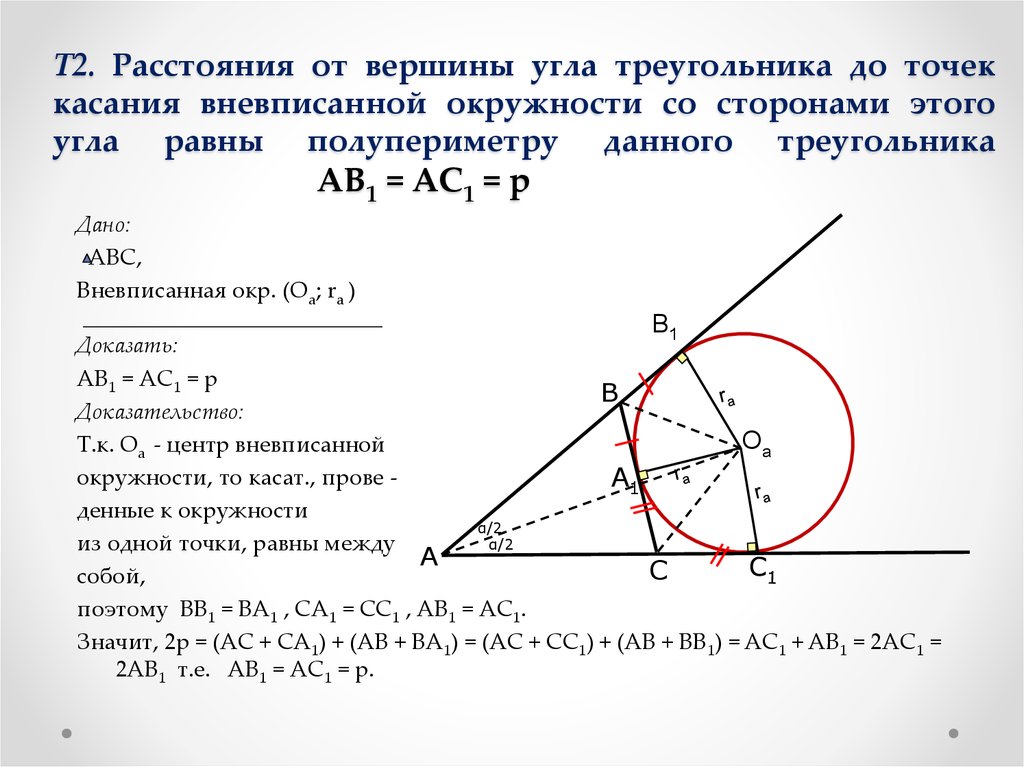
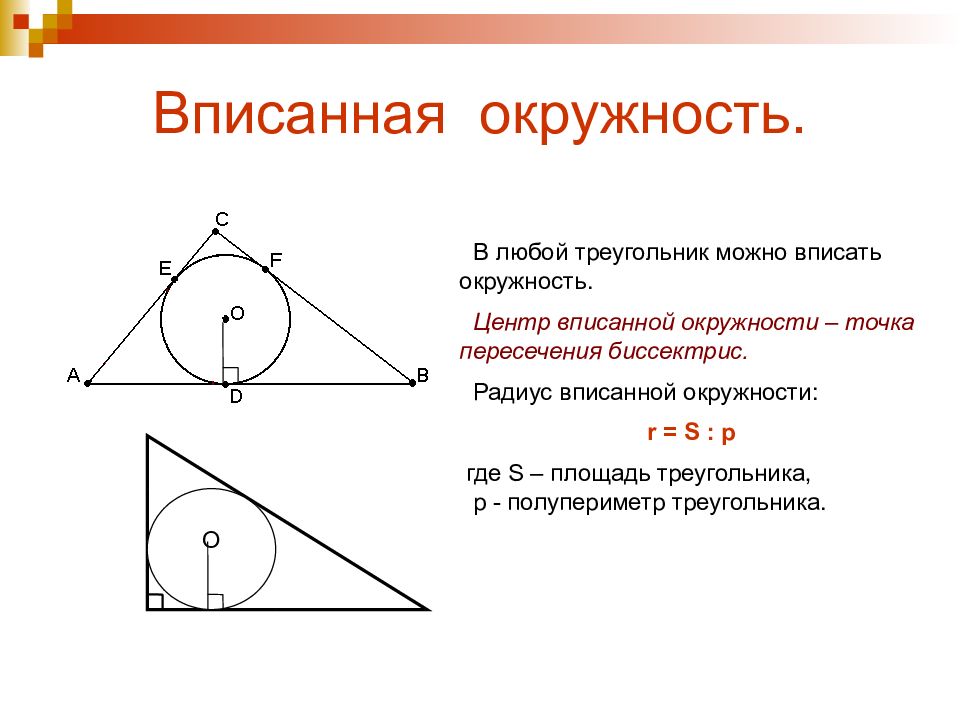
Центр вписанной окружности всегда находится внутри треугольника, на пересечении его биссектрис.

Строим вписанную в данный треугольник окружность (Задача 2).
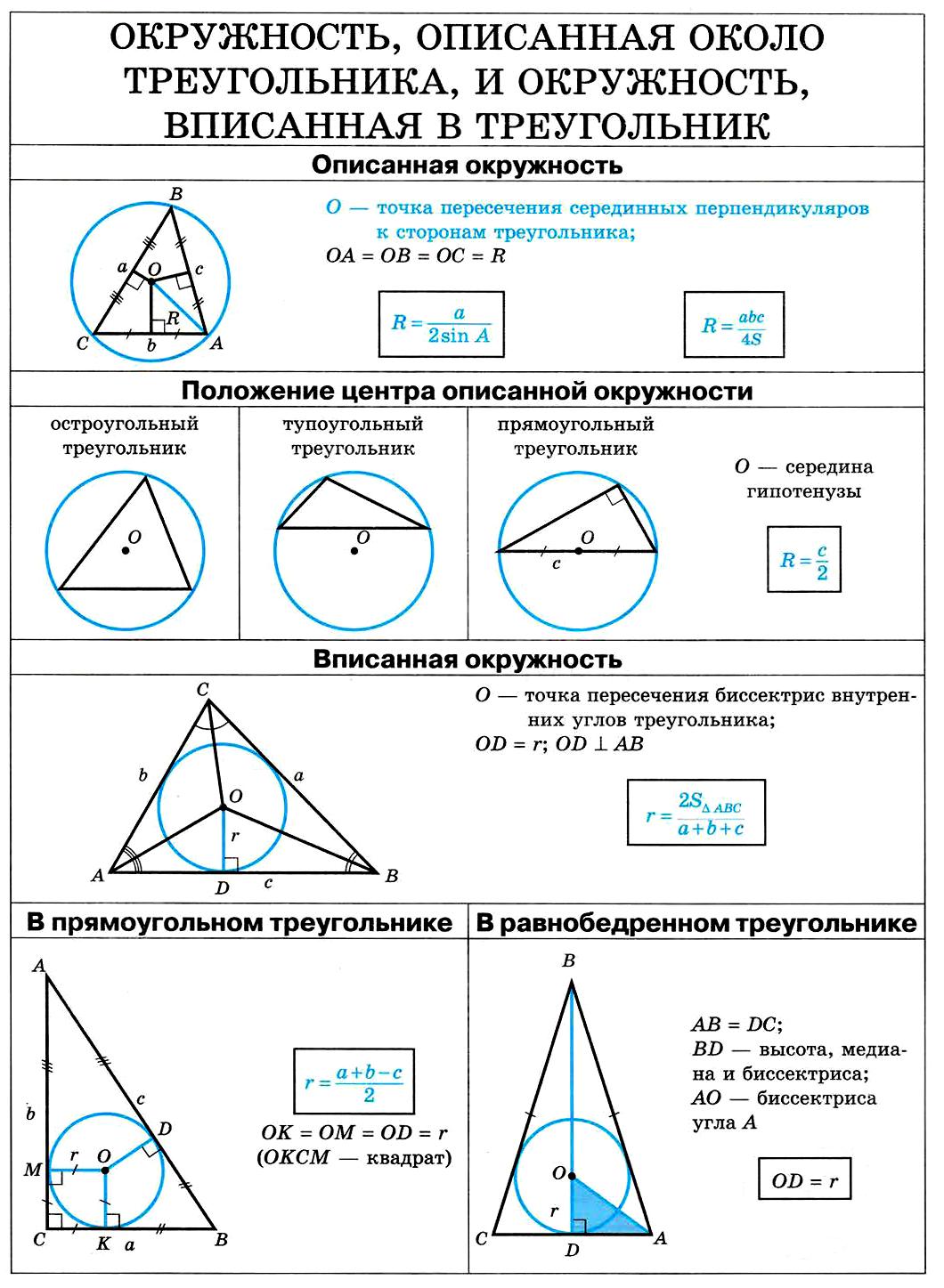

Радиус вписанной окружности можно вычислить, используя формулу: r = S / p, где S - площадь треугольника, p - его полупериметр.

САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математике

Для нахождения касательных, проведите перпендикуляры из центра окружности к каждой стороне треугольника.

Окружность, вписанная в треугольник. Как найти центр и радиус. Геометрия 7-8 класс

Длина касательной от точки касания до вершины треугольника равна отрезку этой стороны минус полупериметр.

Окружность вписанная в треугольник и описанная около треугольника.

Используйте циркуль и линейку для более точного построения окружности и касательных.


Не забывайте проверять точность вычислений, чтобы избежать ошибок при построении.
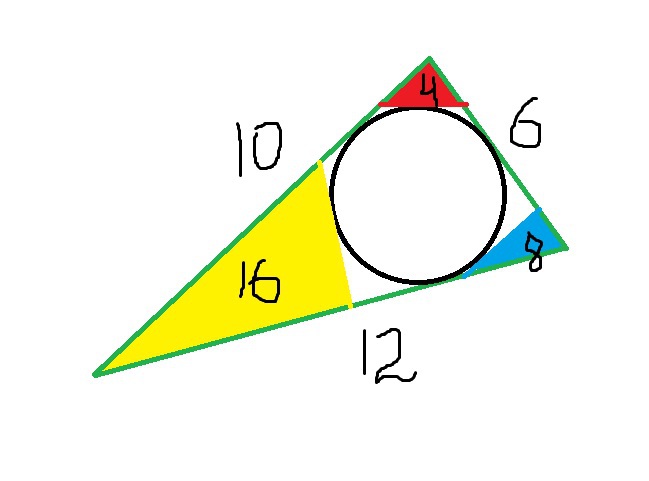
Треугольник с вписанной окружностью имеет особенные свойства, такие как равенство сумм длин касательных от вершин до точек касания.

Всё про углы в окружности. Геометрия - Математика
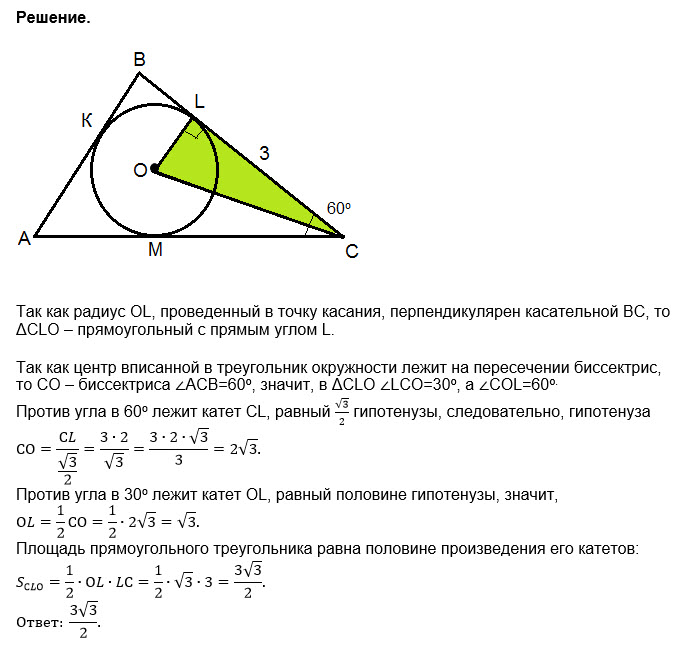
Касательные к вписанной окружности всегда перпендикулярны радиусам, проведенным к точкам касания.
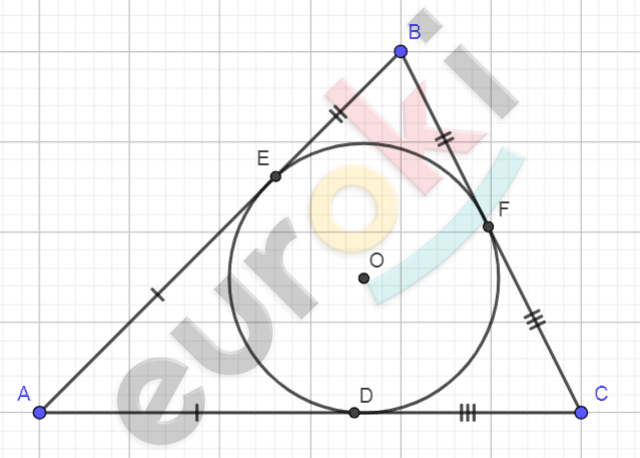
Практикуйтесь на разных типах треугольников, чтобы лучше понять особенности и нюансы вписывания окружностей и построения касательных.

Математика - 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачи

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и Окружность