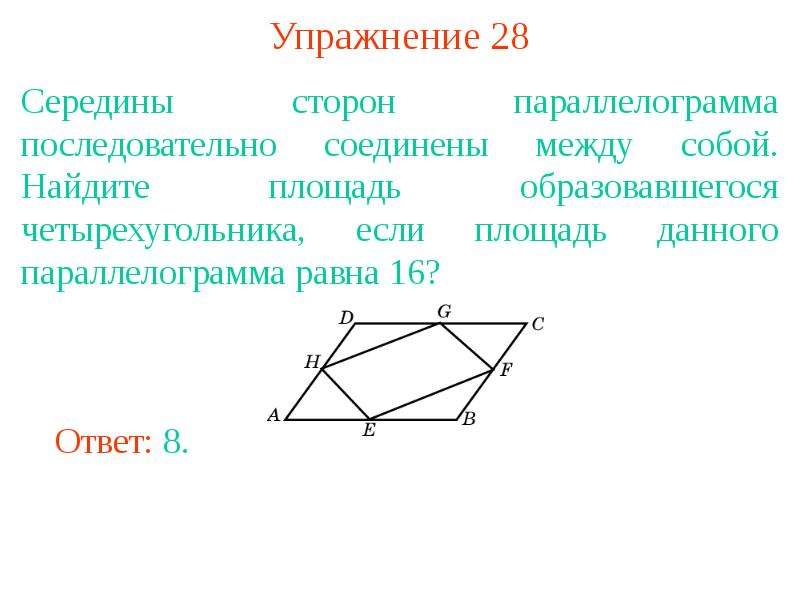
Отрезок, соединяющий середины сторон четырехугольника: советы и примеры
Этот раздел посвящен уникальному геометрическому объекту - отрезку, который соединяет середины сторон четырехугольника. Мы расскажем, как построить этот отрезок, его свойства и полезные советы для изучения геометрии.



Для построения отрезка, соединяющего середины сторон четырехугольника, сначала найдите середины всех сторон и затем соедините их.
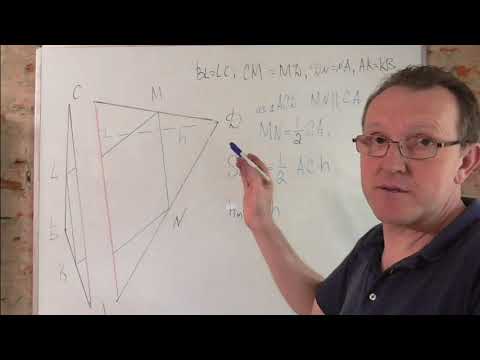
Теорема Вариньона. Середины сторон четырёхугольника.

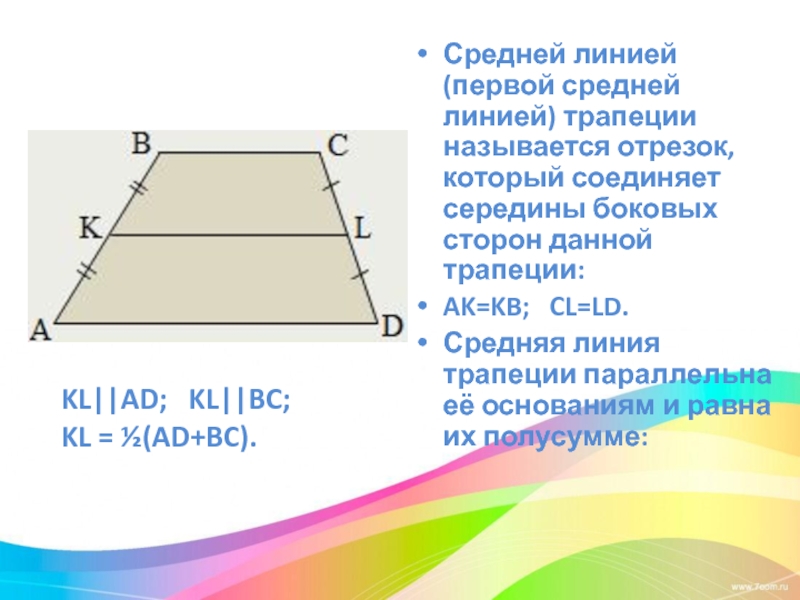
Этот отрезок называется средней линией четырехугольника и обладает уникальными свойствами, такими как параллельность его противоположным сторонам.

23 сентября День Петра и Павла. Что нельзя делать 23 сентября. Народные Приметы и Традиции Дня.
Средняя линия четырехугольника делит его на два равновеликих треугольника.

Самый короткий тест на интеллект Задача Массачусетского профессора
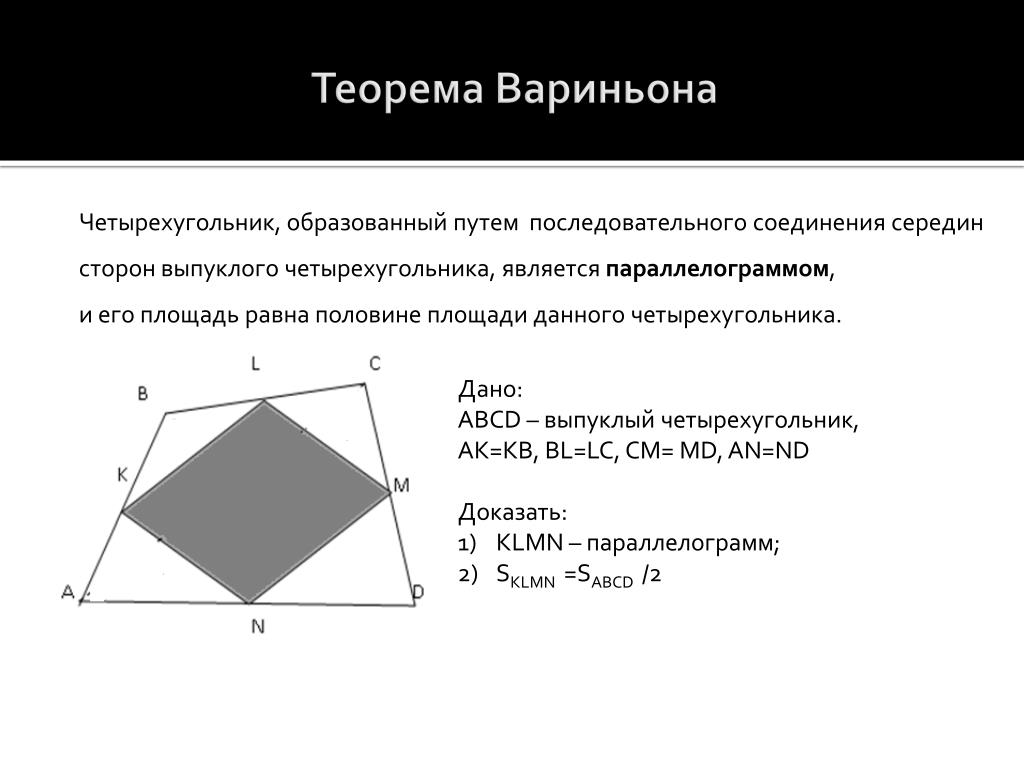
Если четыреугольник является выпуклым, то средняя линия будет параллельна одной из диагоналей четырехугольника.

Геометрическая задача от кандидата
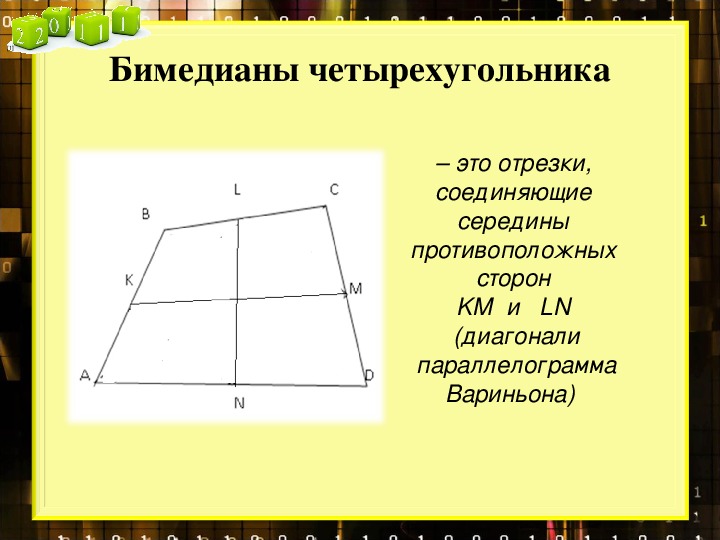
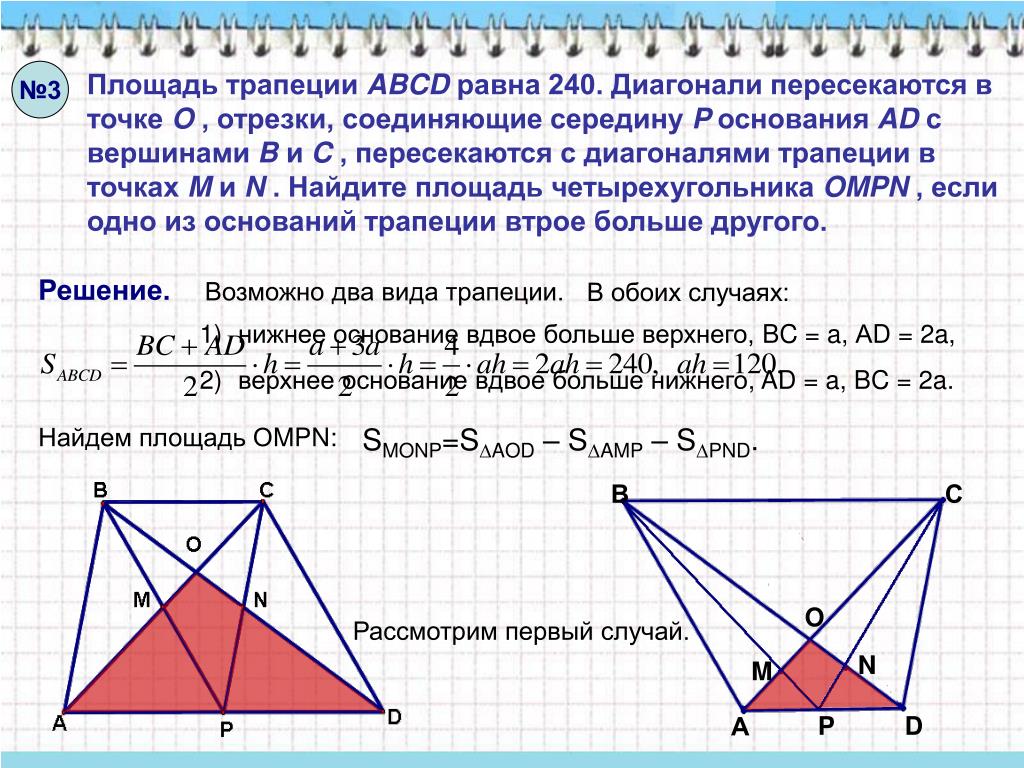
Изучение свойств средней линии четырехугольника помогает глубже понять свойства геометрических фигур и их симметрию.
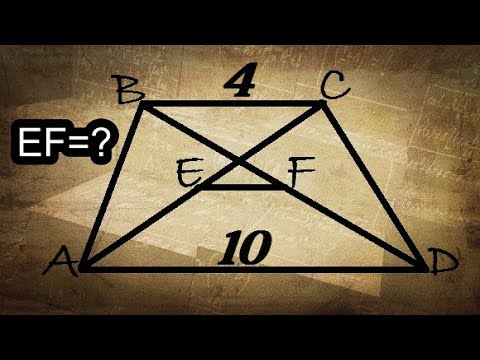
Середины диагоналей трапеции. (Полуразность оснований)
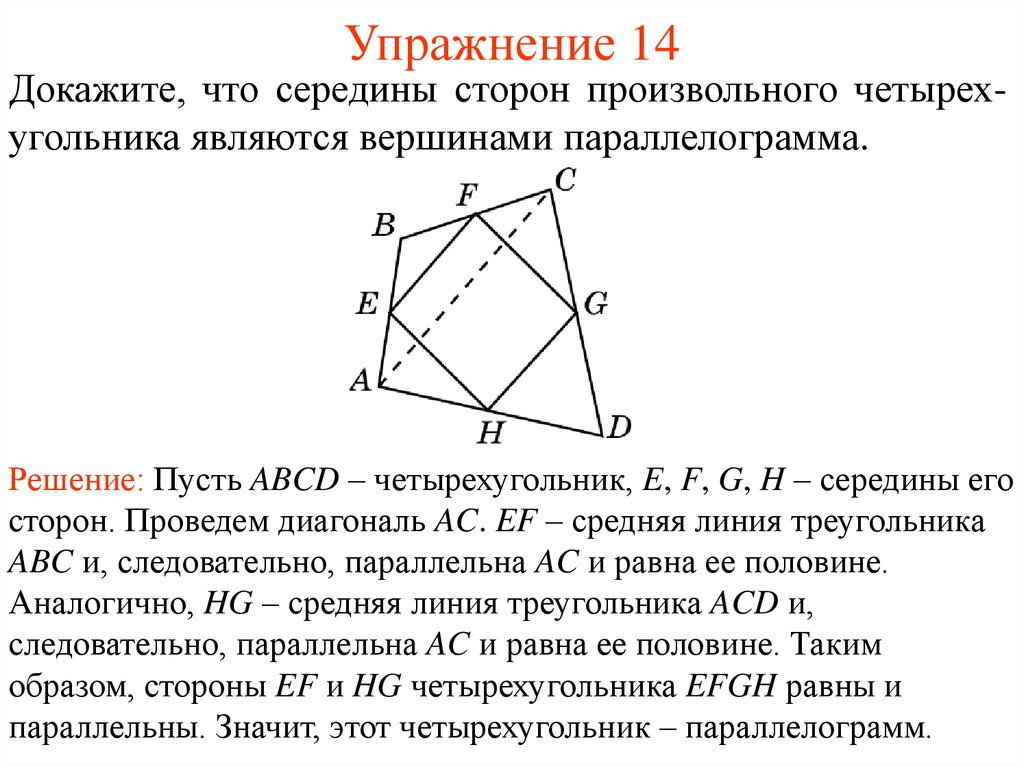
Используйте геометрические инструменты, такие как линейка и циркуль, для точного построения средней линии.
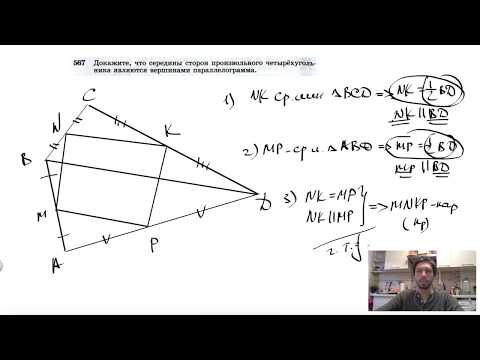
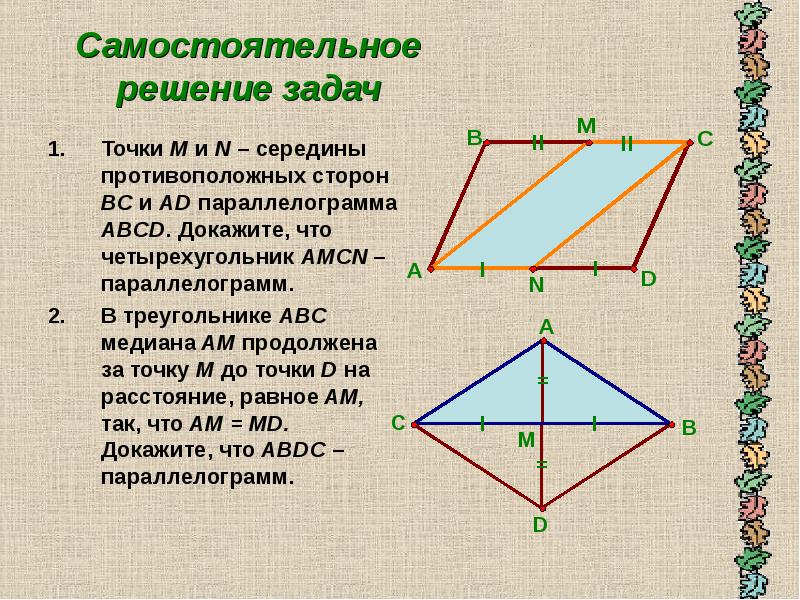
№567. Докажите, что середины сторон произвольного четырехугольника являются
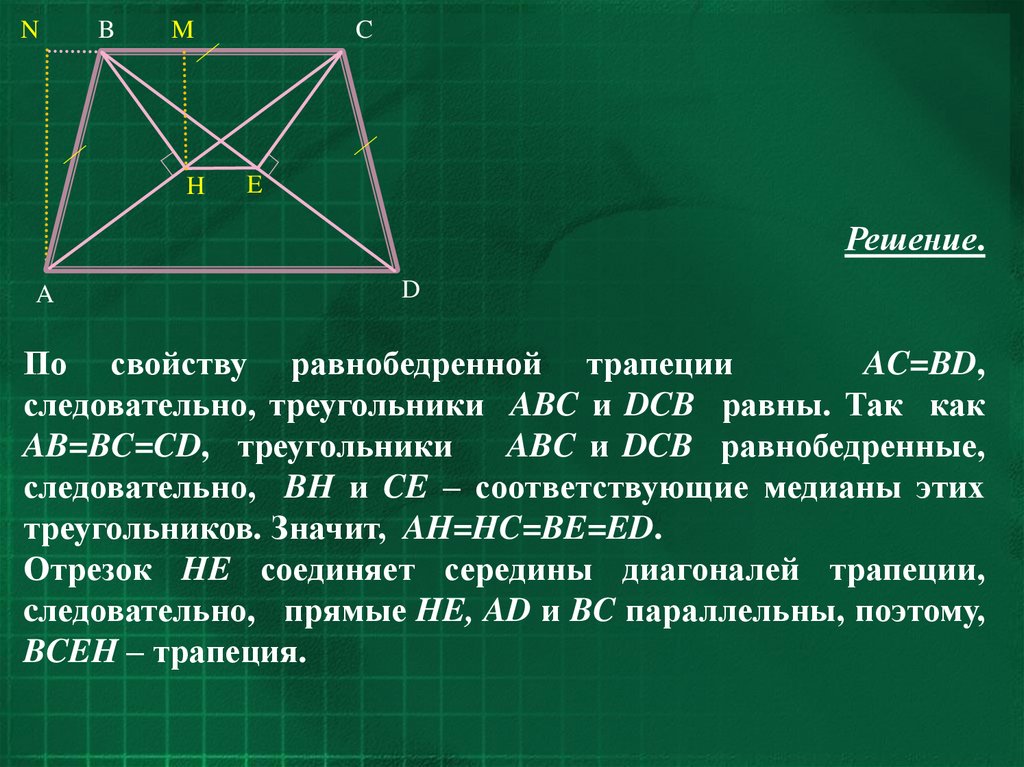
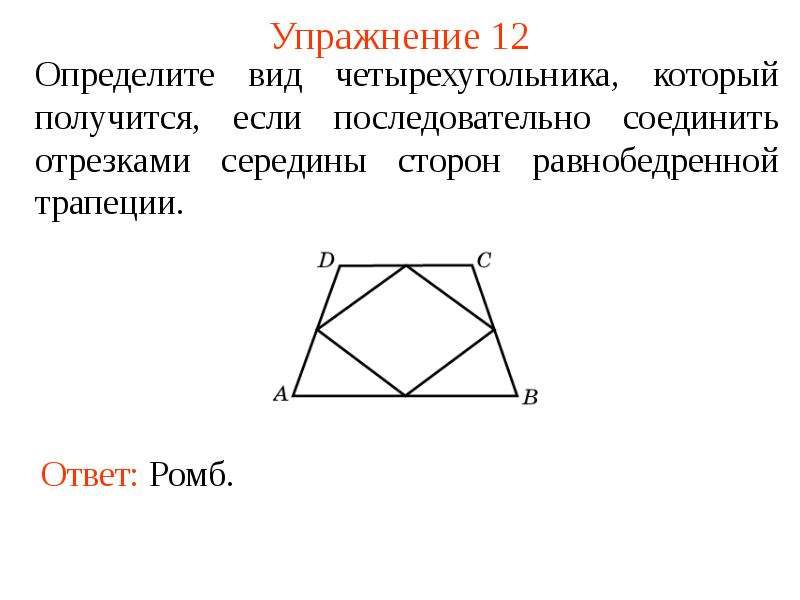
При построении средней линии на компьютере используйте программы, такие как GeoGebra, для точности и наглядности.
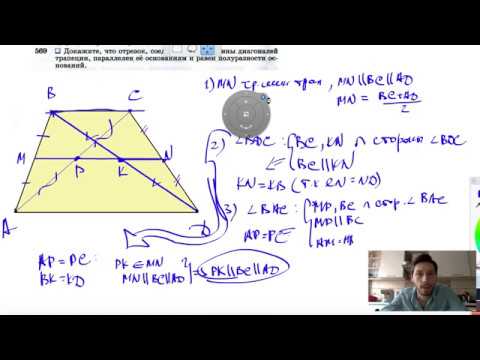
№569. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен

Проведите эксперимент с различными видами четырехугольников, чтобы увидеть, как изменяется средняя линия.

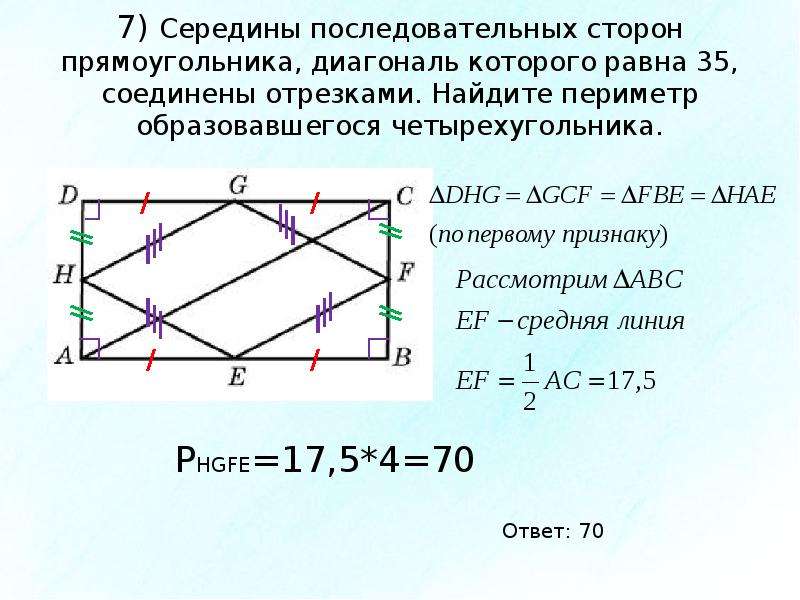
Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольника
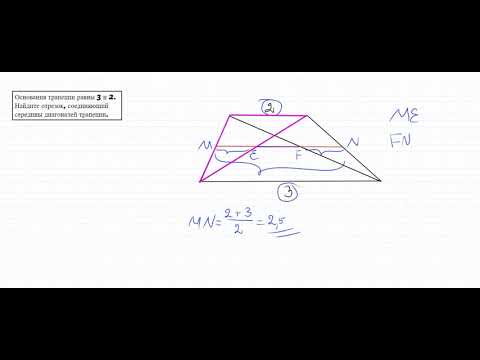
Отрезок, соединяющий середины диагоналей трапеции


Средняя линия четырехугольника может использоваться для решения сложных геометрических задач и доказательства теорем.

Середины сторон произвольного четырехугольника являются вершинами параллелограмма
Понимание свойств средней линии помогает развивать пространственное мышление и математическую интуицию.