Эффективные методы для доказательства пересечения высот в треугольнике
На этой странице вы найдете подборку фотографий и полезных советов по доказательству пересечения высот в треугольнике. Наши советы помогут вам лучше понять и применить данный математический принцип на практике.

Начните с понимания основных свойств высот в треугольнике и их пересечения.

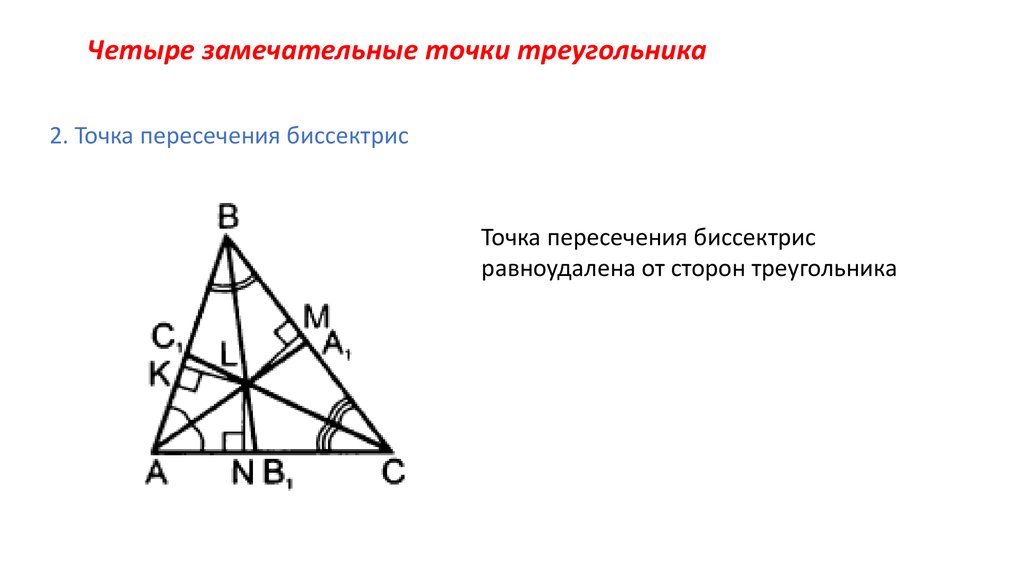
Точка пересечения высот треугольника.
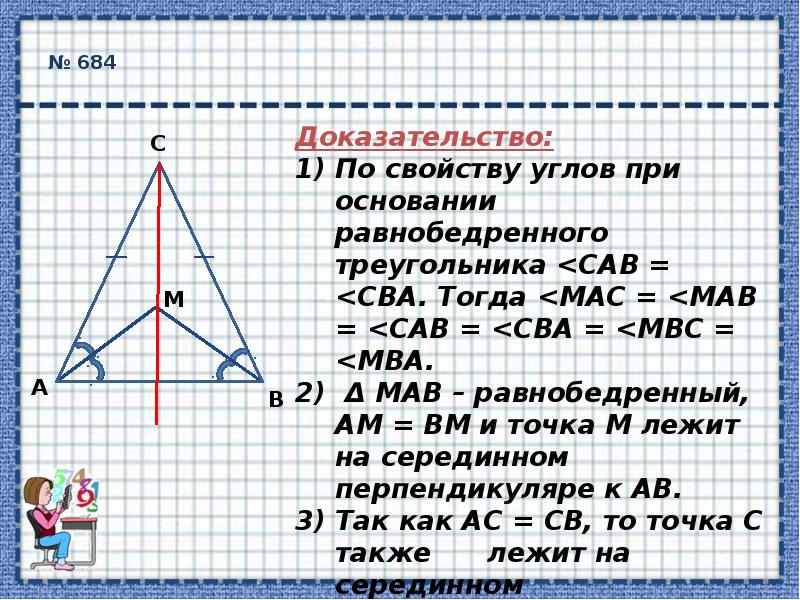
Используйте геометрические инструменты, такие как линейка и транспортир, для точного построения высот.

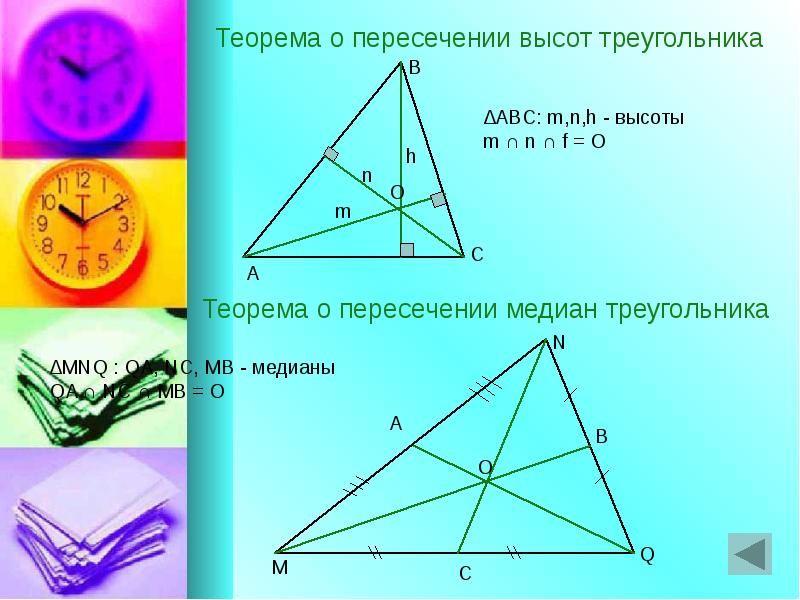
76. Теорема о пересечении высот треугольника
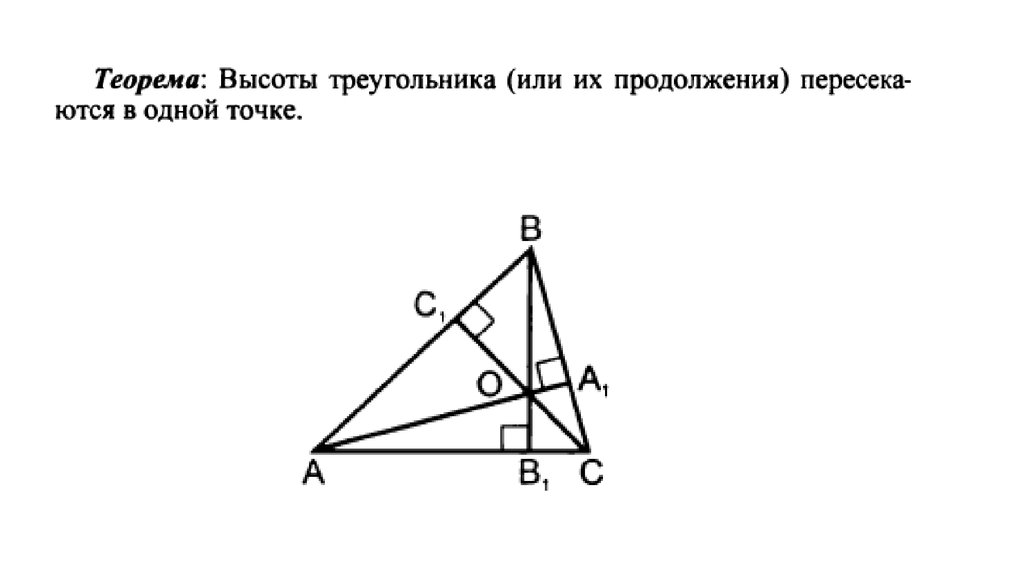
Изучите различные методы доказательства, включая аналитический и синтетический подходы.

Теорема о пересечении высот треугольника - Геометрия 7-9 класс #73 - Инфоурок
Практикуйтесь на разных типах треугольников: остроугольных, тупоугольных и прямоугольных.

8 класс, 37 урок, Теорема о пересечении высот треугольника

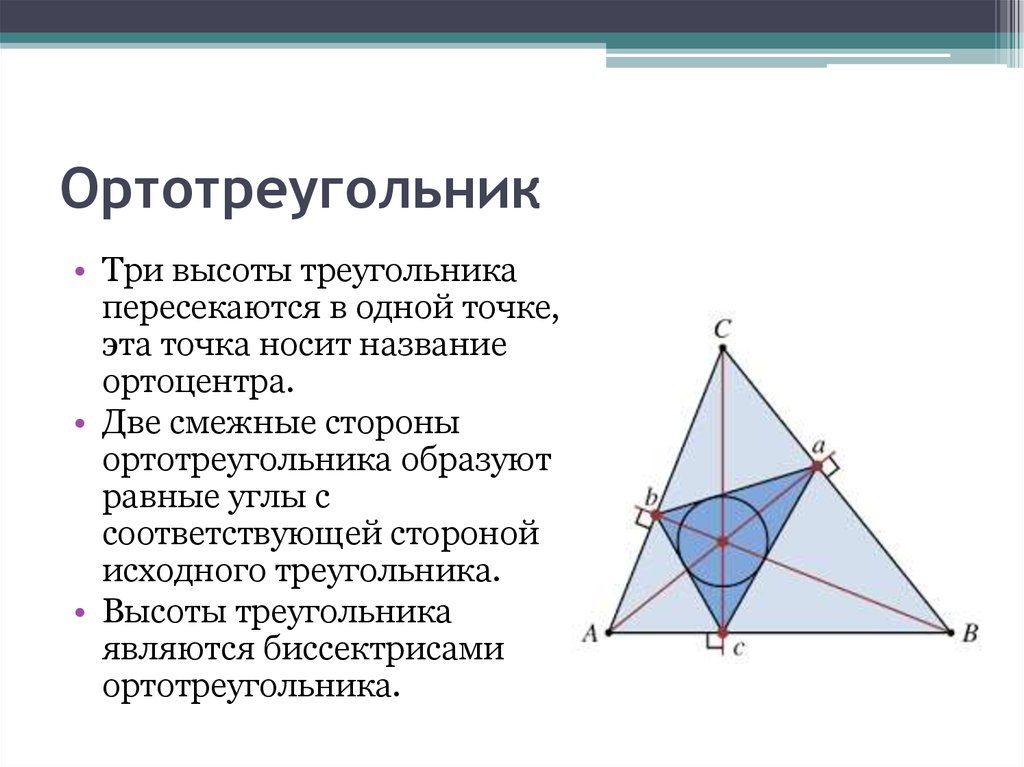
Помните, что точка пересечения высот называется ортоцентром и всегда находится внутри треугольника, если треугольник остроугольный.

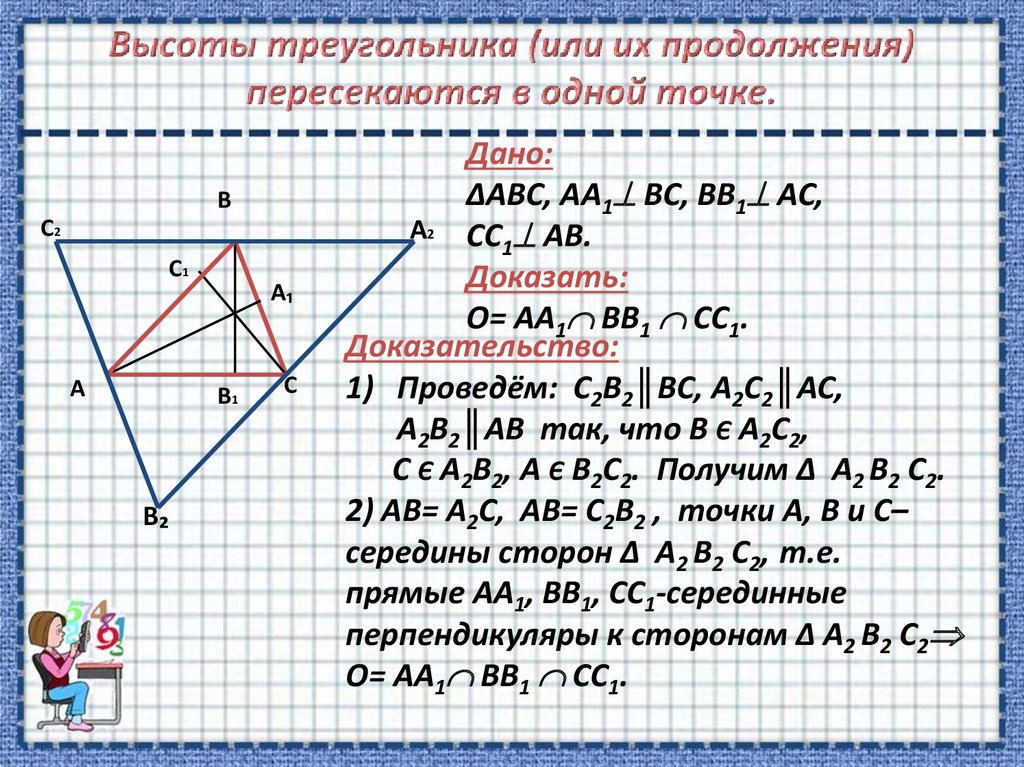
Новое доказательство пересечения высот треугольника в одной точке
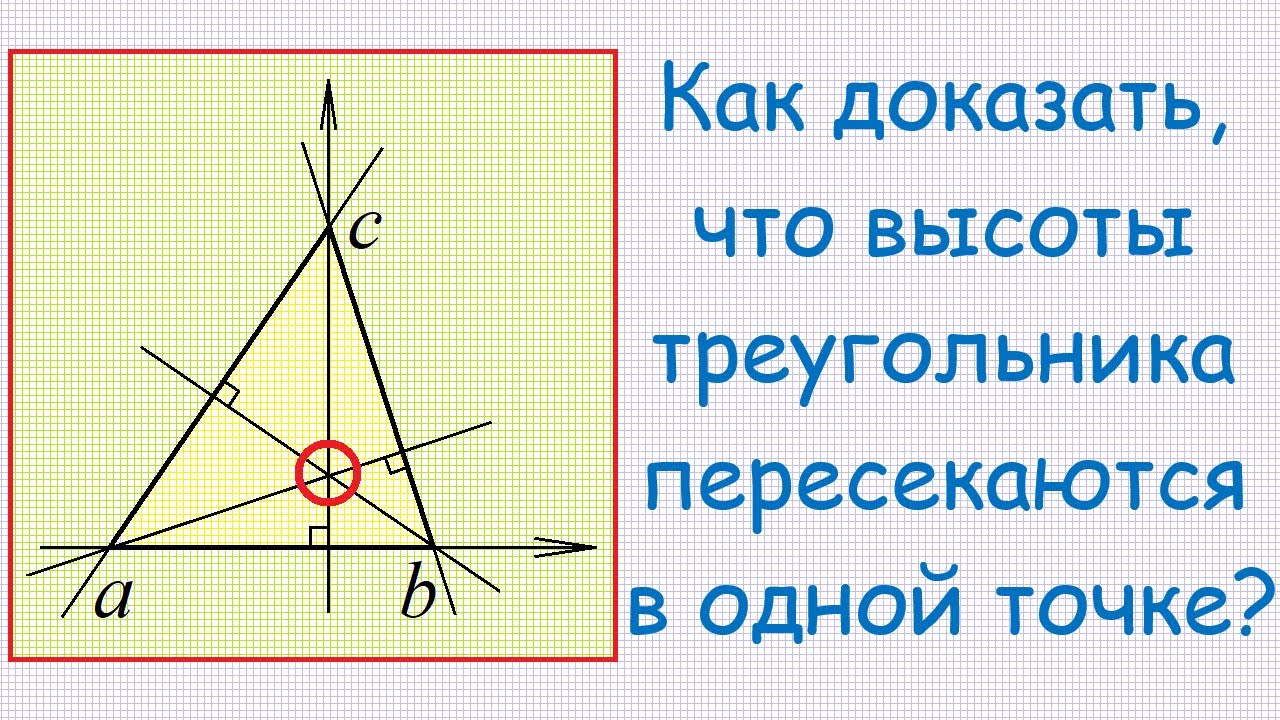
Для тупоугольных треугольников ортоцентр будет находиться вне треугольника.

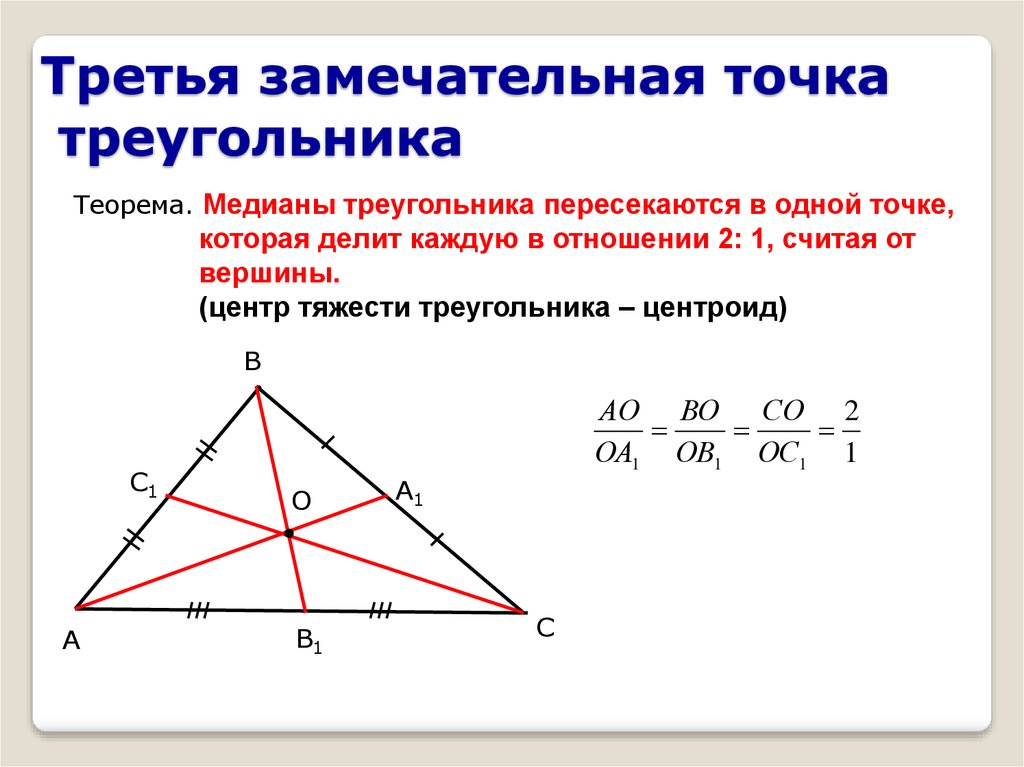
Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.

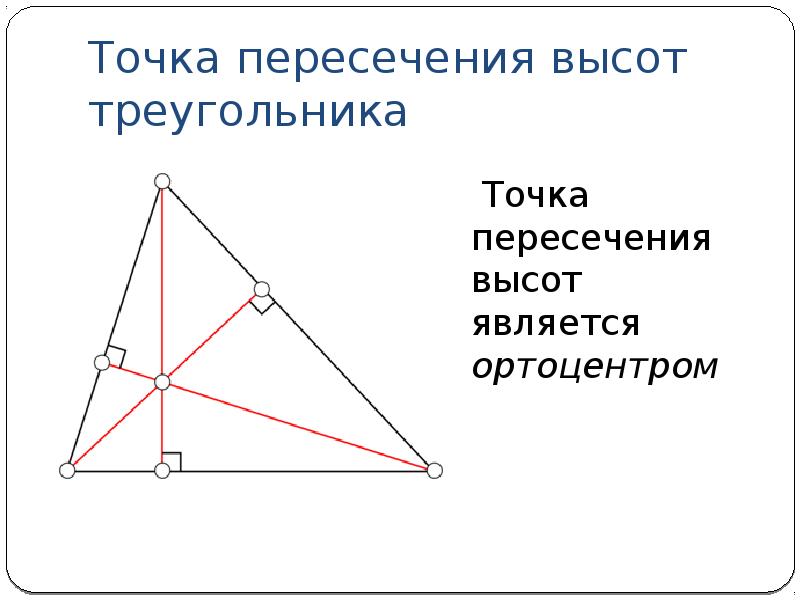
В прямоугольных треугольниках ортоцентр совпадает с вершиной прямого угла.
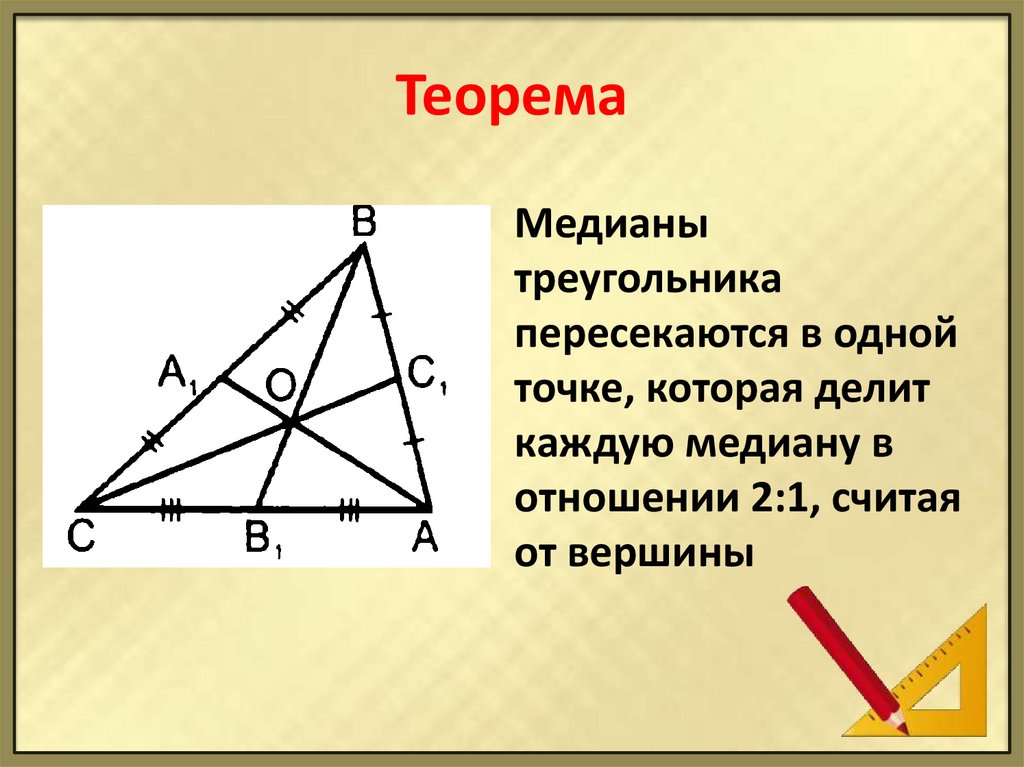
Используйте цветные карандаши или маркеры для обозначения высот и их пересечения на рисунке.
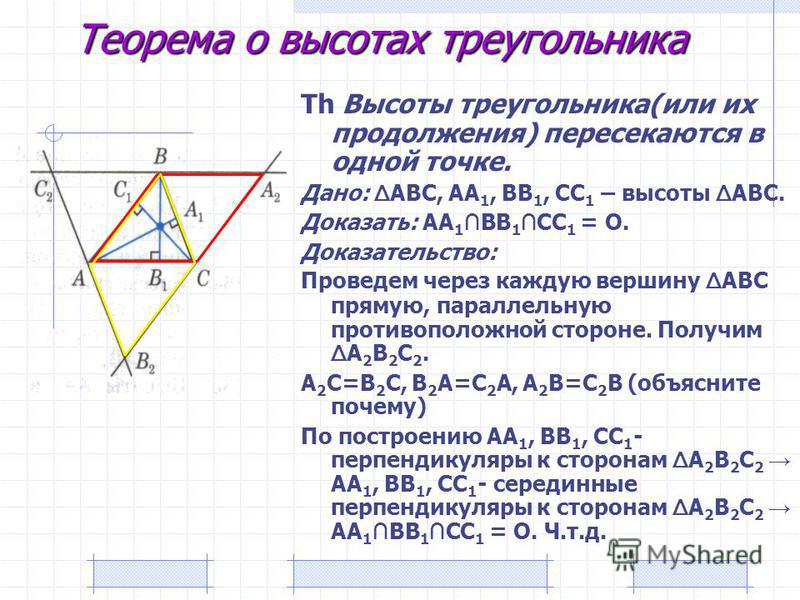
Не забывайте проверять свои построения, чтобы убедиться в их точности.
Регулярно практикуйтесь, решая задачи из учебников и других источников.