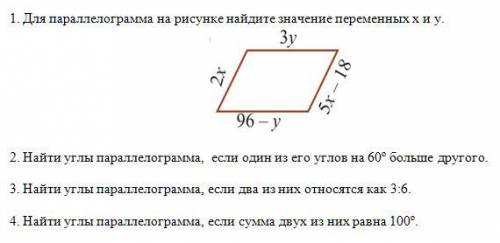
Практическое руководство по вычислению площади параллелограмма на основе векторов
Изучите, как определить площадь параллелограмма, построенного на двух векторах, с помощью простых и наглядных примеров, а также полезных советов для облегчения вычислений.

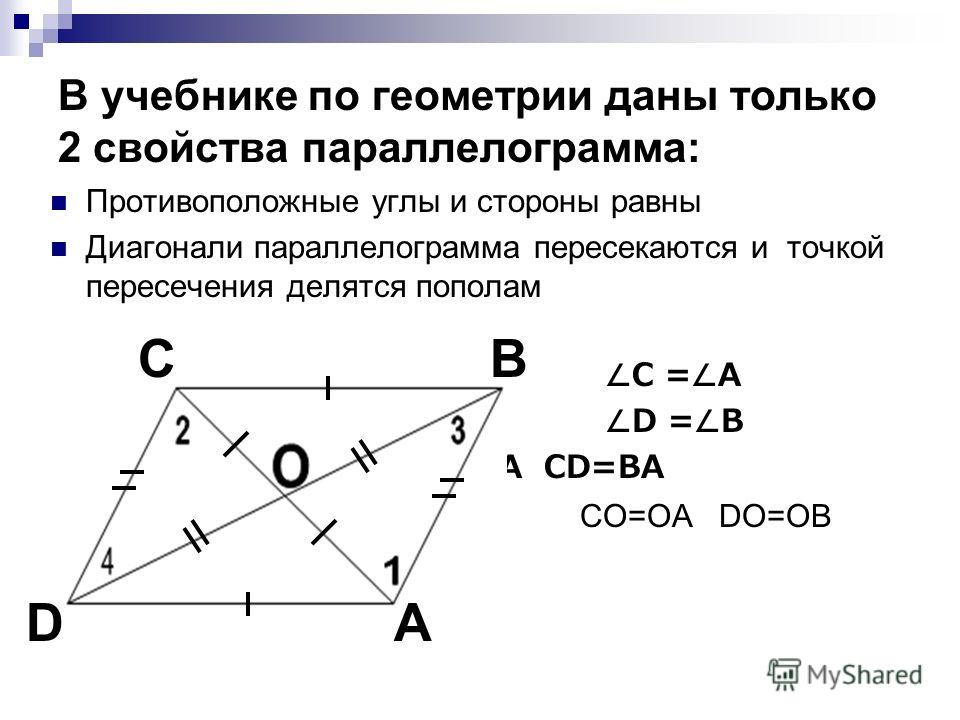
Для расчета площади параллелограмма используйте формулу: |a × b|, где a и b - векторы.
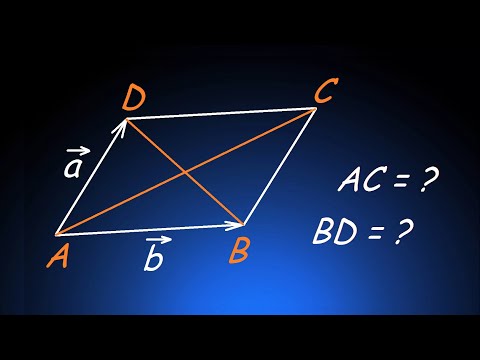
Найдите длины диагоналей параллелограмма, построенного на векторах a=(1;-1;-4) и b=(-5;3;8)

Помните, что результат произведения векторов - это вектор, перпендикулярный плоскости, на которой они лежат.

Решение, вычислить площадь параллелограмма построенного на векторах a и b пример 7 Высшая математика
Для упрощения вычислений используйте координатный метод: |a × b| = |a1 * b2 - a2 * b1| для векторов в двумерном пространстве.

Площадь параллелограмма по векторам


При работе в трехмерном пространстве применяйте детерминант: |a × b| = sqrt((a2b3 - a3b2)^2 + (a3b1 - a1b3)^2 + (a1b2 - a2b1)^2).

Решение, вычислить площадь параллелограмма построенного на векторах a и b пример 5 Высшая математика

Убедитесь, что вы правильно определили компоненты векторов перед началом расчетов.

Решение, найти площадь параллелограмма, построенного на векторах a и b пример 3. Высшая математика.
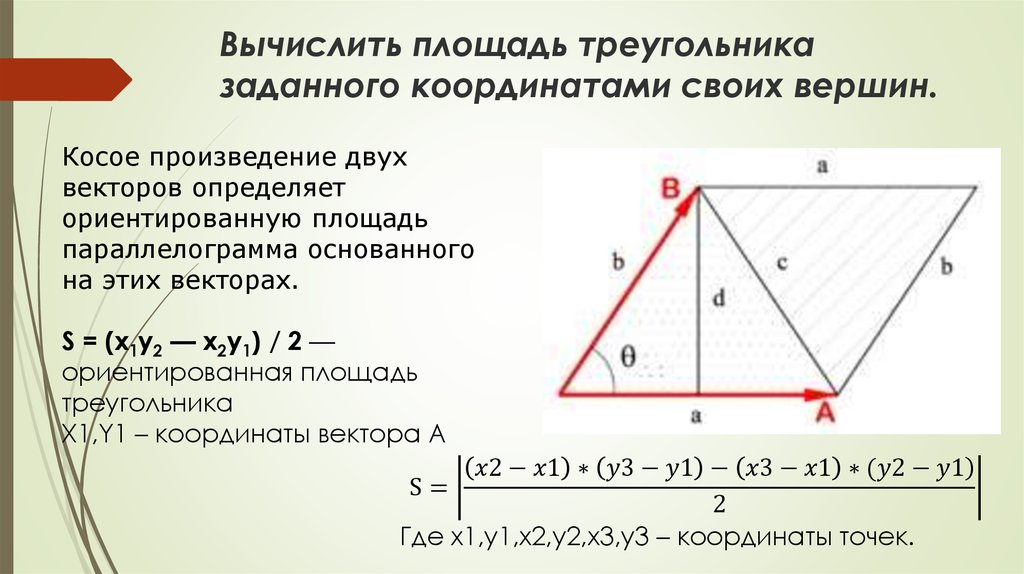
Используйте векторное произведение, чтобы найти направление нормального вектора к плоскости параллелограмма.

как найти площадь параллелограмма построенного на векторах

Проверяйте промежуточные результаты, чтобы избежать ошибок в финальных расчетах.

Решение, вычислить площадь параллелограмма, построенного на векторах а и b пример 1
Если вы используете программные средства для вычислений, убедитесь в их правильной настройке и точности.

Найти площадь параллелограмма, построенного на векторах a=p−3q и b=p+2q; -p-=1/5, -q-=1 пример 16
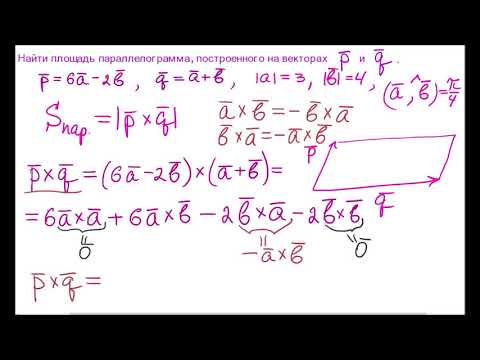
Площадь параллелограмма, построенного на данных векторах
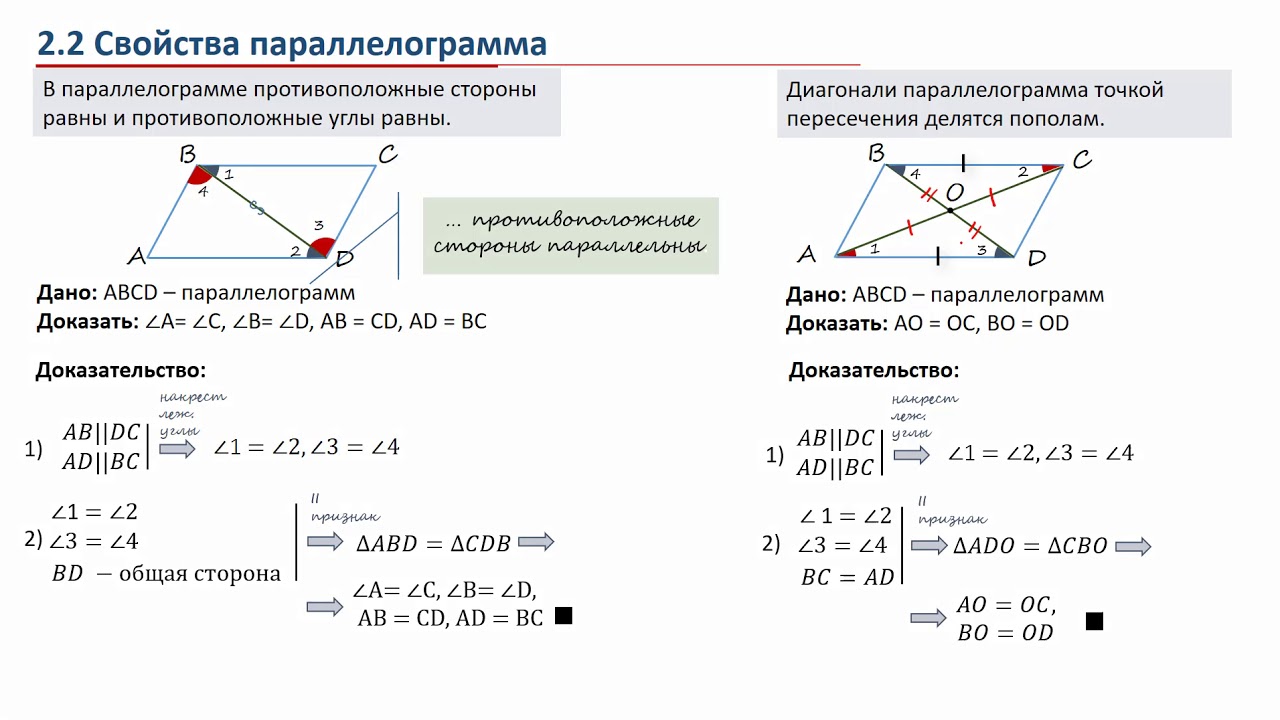

Для визуализации результатов используйте графические программы, чтобы увидеть геометрическую интерпретацию параллелограмма.

Найдите площадь параллелограмма, построенного на векторах


Не забывайте проверять размерности всех величин, чтобы избежать ошибок в расчетах и интерпретации результата.