Радиус вписанной окружности в треугольнике: лучшие методы и фотографии
На этой странице вы найдете подборку фотографий и полезных советов о том, как определить радиус окружности, вписанной в треугольник. Мы предлагаем простые и эффективные методы, которые помогут вам в решении геометрических задач.
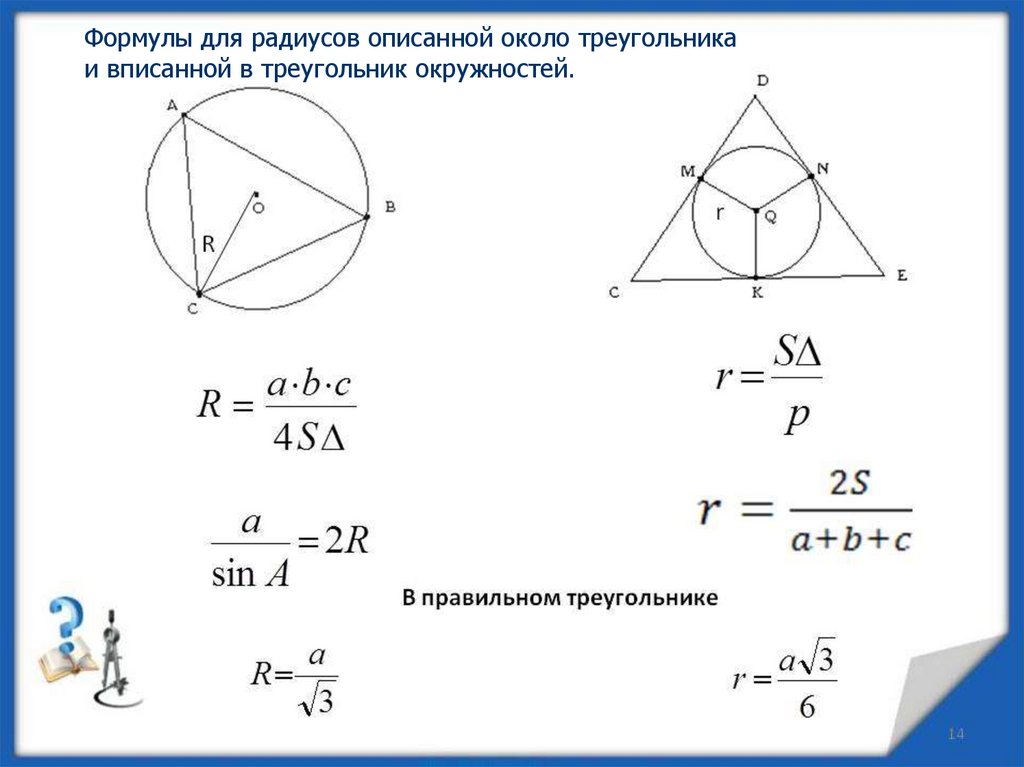

Используйте формулу радиуса вписанной окружности: r = A / s, где A - площадь треугольника, s - полупериметр.

Подобие треугольников Радиус вписанной окружности

Для нахождения полупериметра сложите все стороны треугольника и разделите на два.

как найти радиус вписанной окружности - #егэ #профильнаяматематика #егэпрофиль
Площадь треугольника можно найти по формуле Герона: A = √(s(s-a)(s-b)(s-c)), где a, b, c - стороны треугольника.

ПЛОЩАДЬ ТРЕУГОЛЬНИКА через радиус вписанной окружности

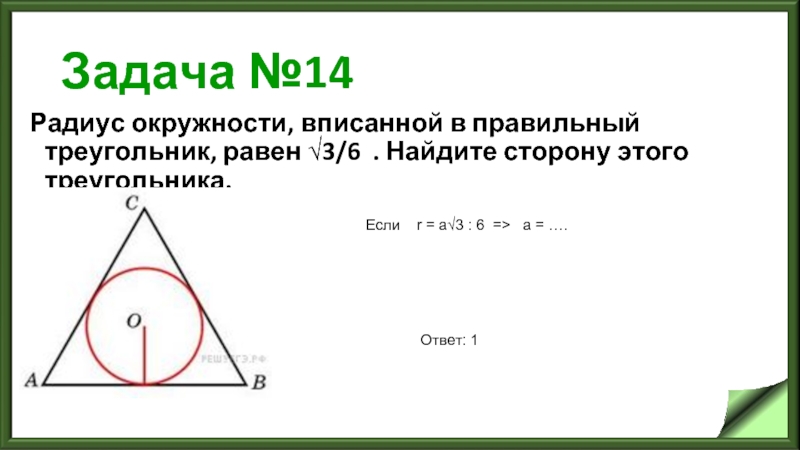
В равностороннем треугольнике радиус вписанной окружности можно найти по формуле: r = a√3 / 6, где a - сторона треугольника.

Построить описанную окружность (Задача 1)


Для прямоугольного треугольника используйте формулу: r = (a + b - c) / 2, где a и b - катеты, c - гипотенуза.
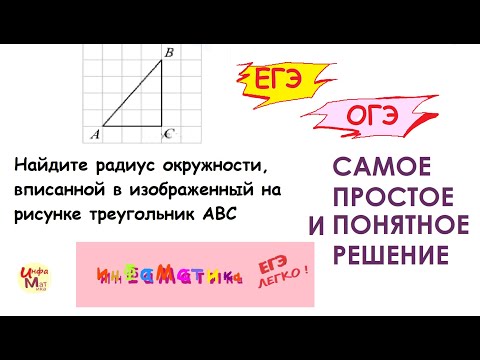
Найдите радиус окружности, вписанной в изображенный на рисунке треугольник ABC
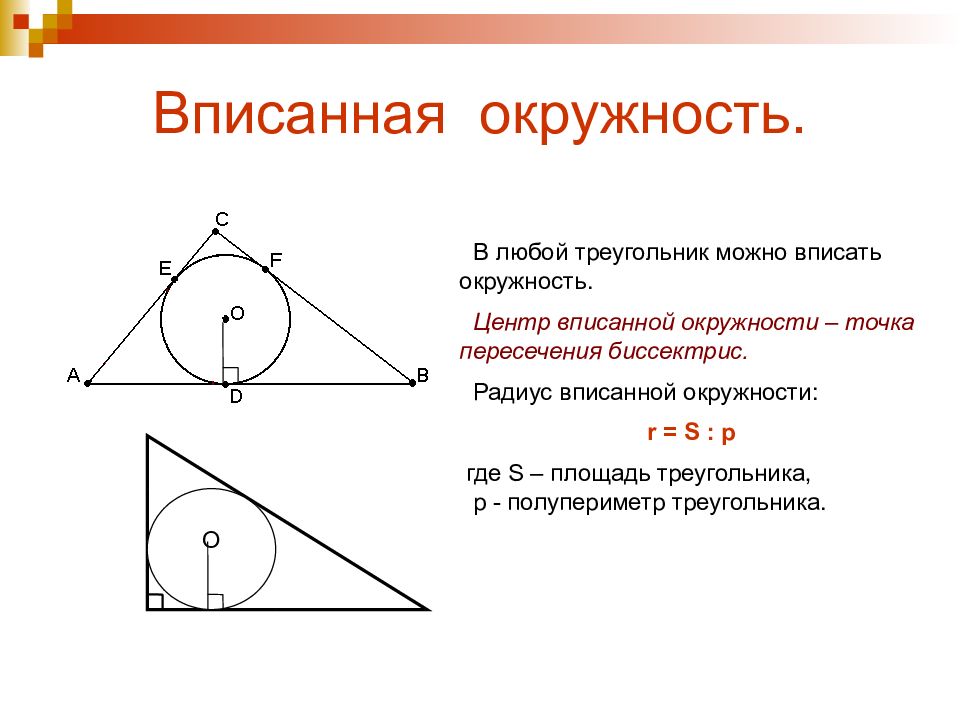
Проверяйте точность своих вычислений, используя разные методы для сравнения результатов.

Окружность вписанная в треугольник и описанная около треугольника.
Не забывайте учитывать точность измерений сторон треугольника, так как это влияет на точность результата.

Строим вписанную в данный треугольник окружность (Задача 2).
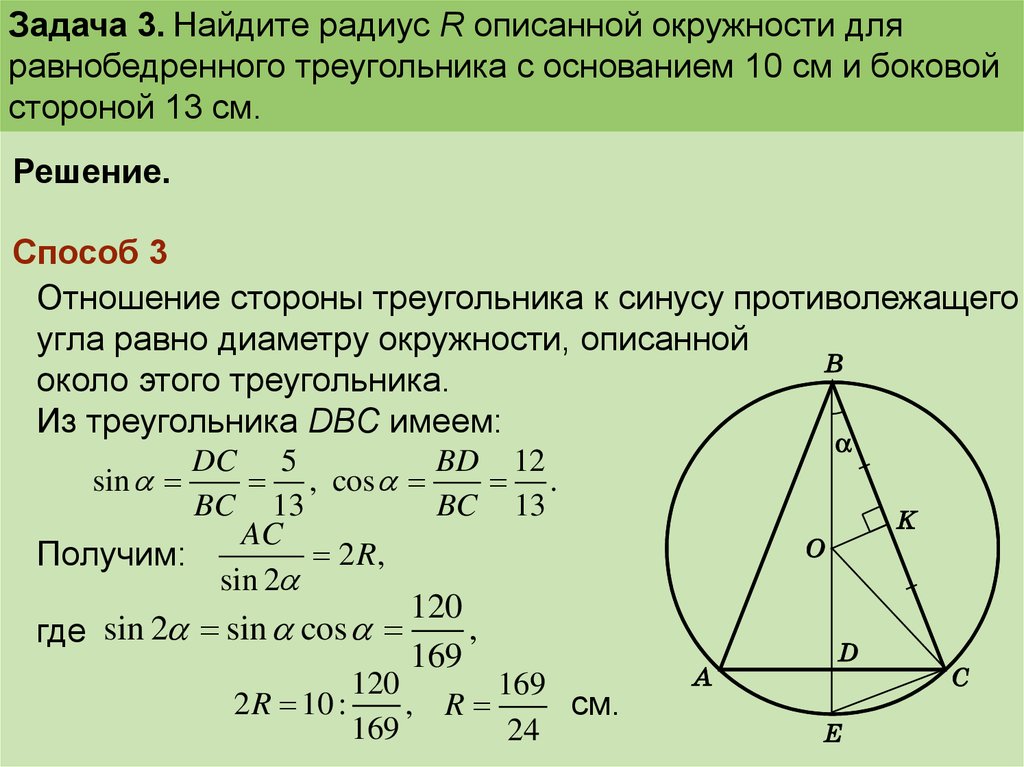

Используйте графические программы или калькуляторы для проверки своих расчетов.
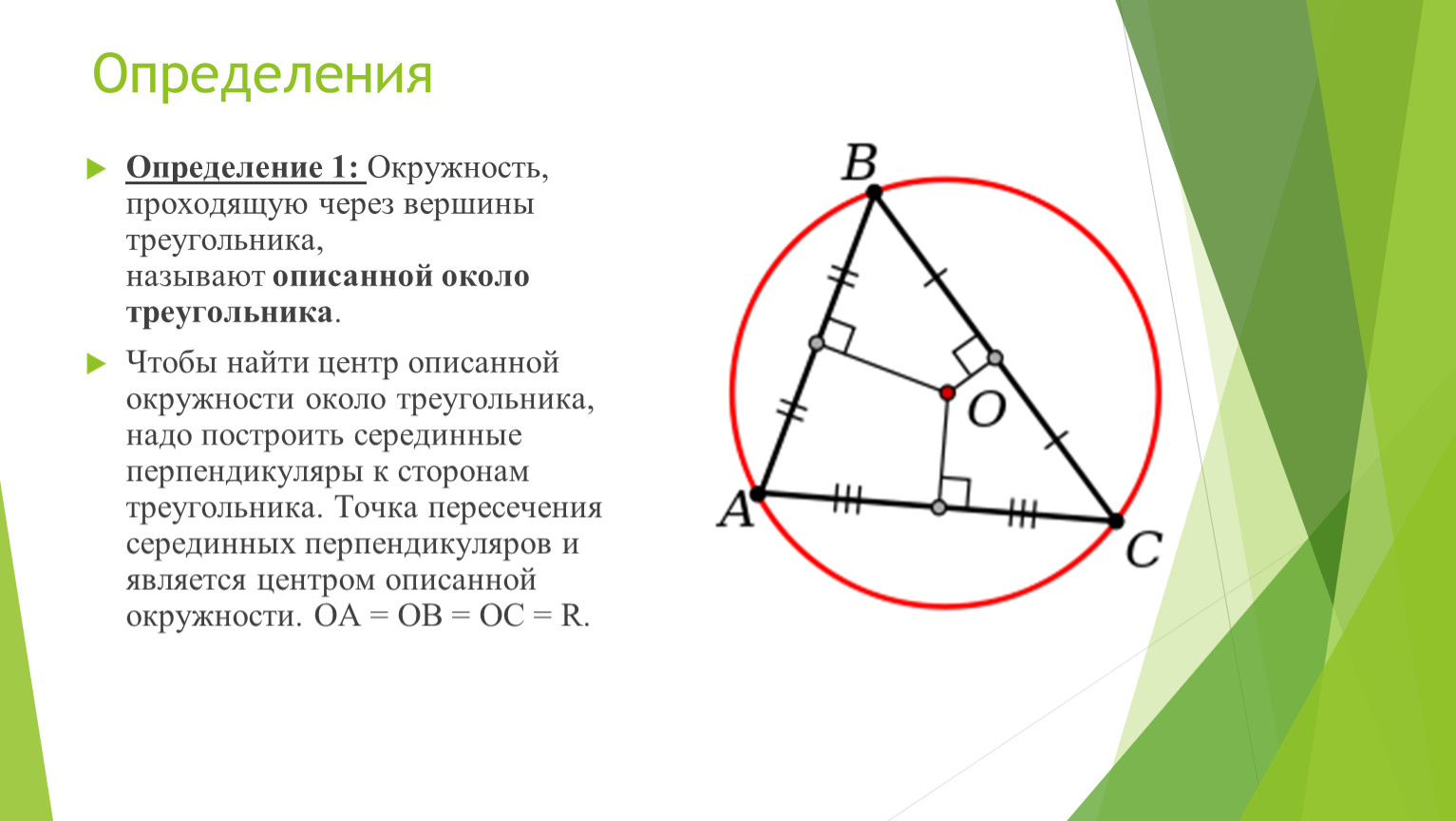
Внимательно изучайте свойства различных типов треугольников, чтобы правильно применять соответствующие формулы.
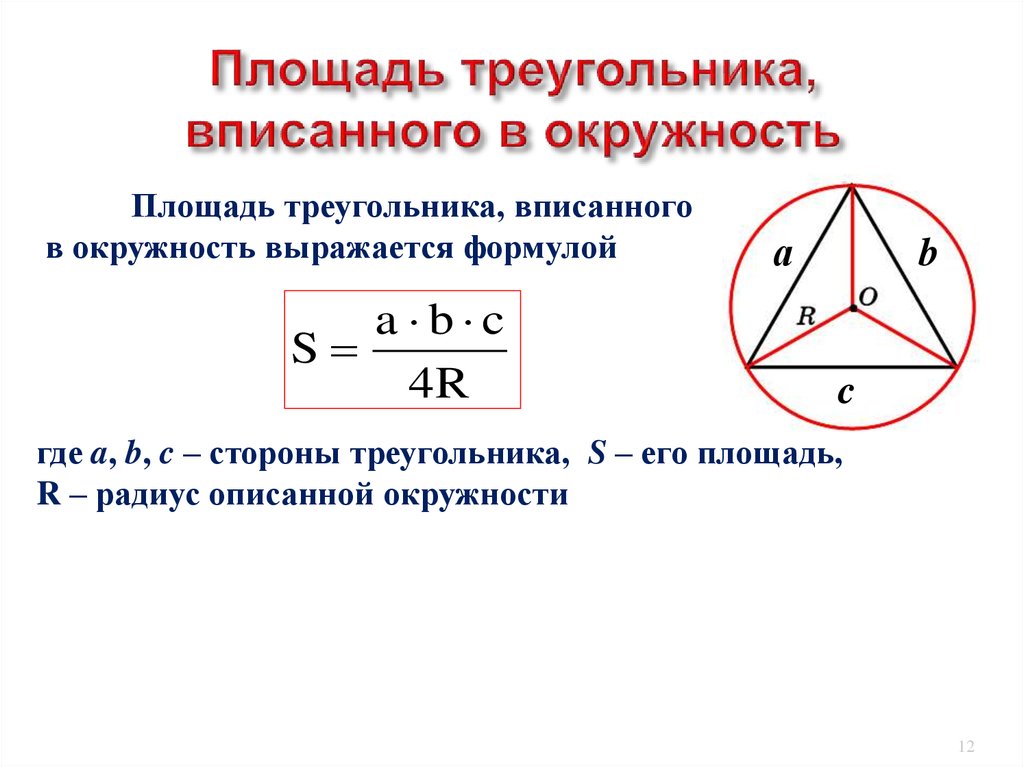
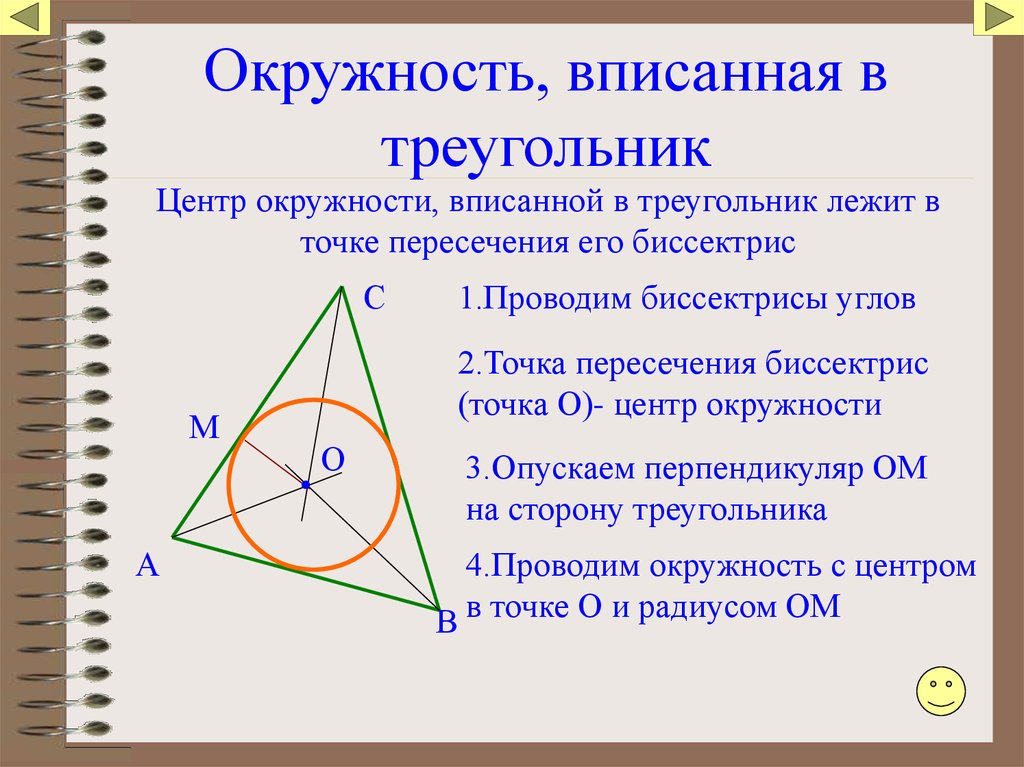
Практикуйтесь на разных примерах и задачах, чтобы лучше понимать процесс нахождения радиуса вписанной окружности.
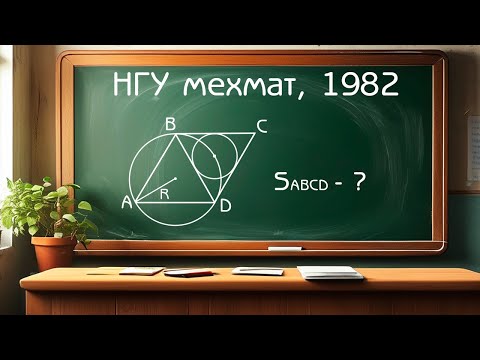
Вступительный экзамен НГУ мехмат 1982 год - Задача по планиметрии
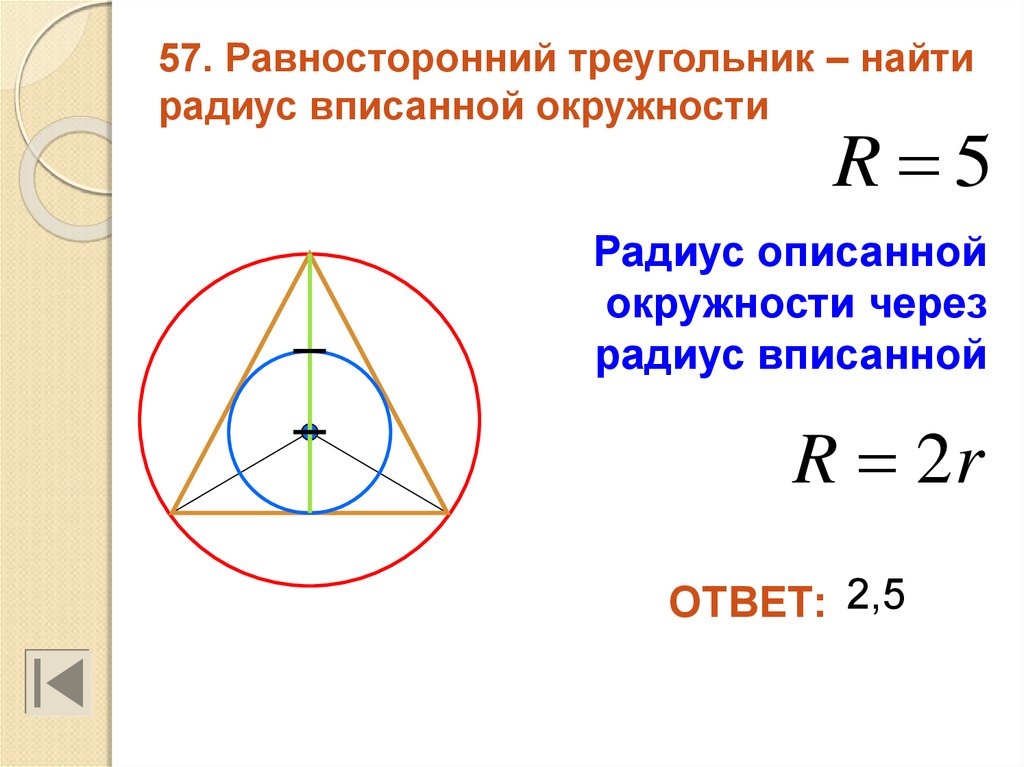
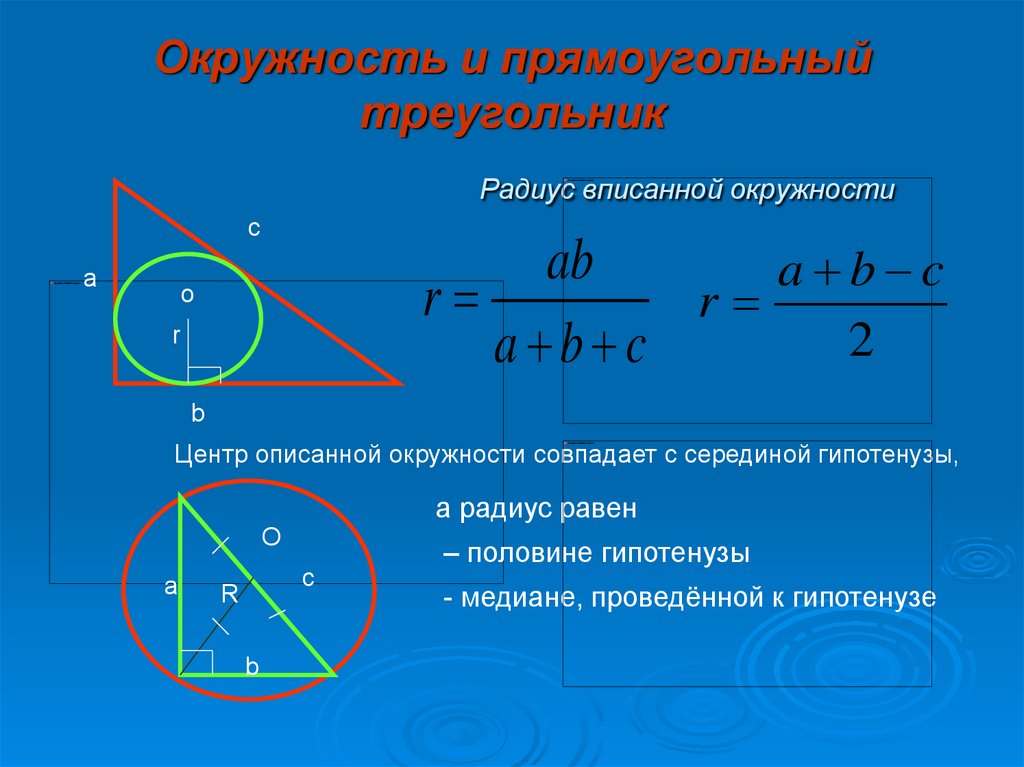

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.