Практическое руководство по методу Зейделя для решения линейных уравнений
На этой странице вы найдете полезные советы и иллюстрации по решению систем линейных уравнений методом Зейделя. Метод Зейделя, также известный как метод последовательных приближений, является эффективным способом нахождения решений систем линейных уравнений, особенно при больших размерах систем. В данном разделе представлены ключевые рекомендации и наглядные примеры, которые помогут вам овладеть этим методом.



Начните с приведения системы линейных уравнений к диагонально доминирующей форме для повышения сходимости метода Зейделя.

Метод простой итерации Пример Решения


Инициализируйте начальные приближения для всех переменных; обычно это набор нулей или другие простые значения.
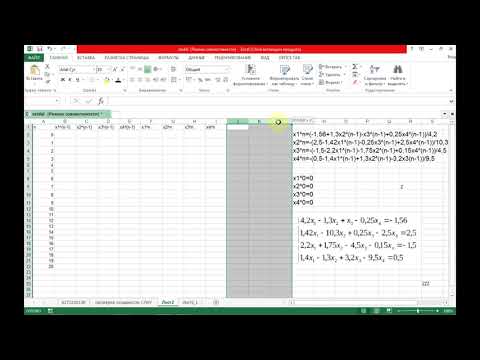
Метод_Зейделя_Excel


Следите за изменениями в значениях переменных на каждой итерации, чтобы убедиться в сходимости к точному решению.

Метод Зейделя

Используйте критерий остановки, основанный на заданной точности или максимальном количестве итераций.

Решение системы трёх линейных уравнений методом Зейделя на VBA

Проверяйте правильность промежуточных расчетов, чтобы избежать накопления ошибок.
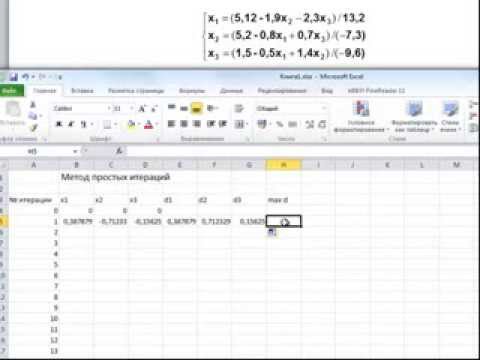
Решение систем линейных уравнений, урок 5/5. Итерационные методы
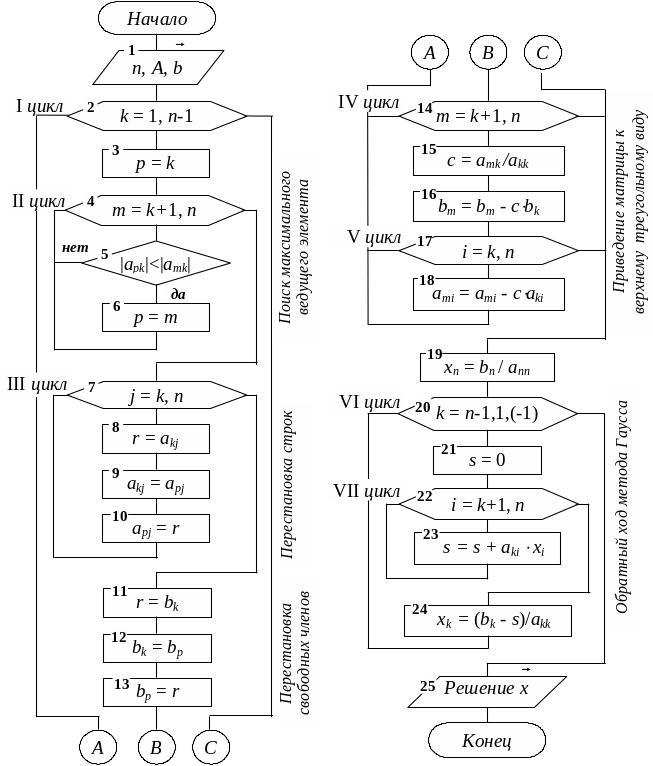

Если метод не сходится, попробуйте переформулировать систему уравнений или изменить начальные приближения.

Эту задачу могут решить лишь единицы
Для ускорения процесса можно использовать релаксацию, увеличивая или уменьшая шаг изменения переменных.

Метод Зейделя Пример Решения

Обязательно документируйте каждый шаг решения для последующего анализа и исправления возможных ошибок.

6 Метод Зейделя Блок-схема Mathcad Calc Excel Решение системы линейных уравнений СЛАУ

9 Метод Зейделя Ручной счет Решение системы линейных уравнений СЛАУ

Сравните полученные результаты с другими методами решения для проверки точности и надежности.
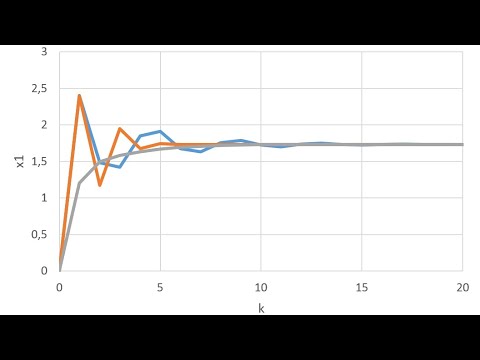
2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)

Изучите примеры и задачи из учебников и научных статей для лучшего понимания и практического применения метода Зейделя.