Теорема Гаусса в интегральной форме: ключевые аспекты и применение
Теорема Гаусса в интегральной форме является одной из фундаментальных теорем векторного анализа и электродинамики. Она описывает связь между потоком вектора через замкнутую поверхность и интегралом дивергенции этого вектора по объему, ограниченному этой поверхностью. В данной подборке представлены фотографии и полезные советы для лучшего понимания и применения теоремы Гаусса.



Изучите основные понятия векторного анализа, такие как дивергенция, поток и поверхность.

Лекция 2.1. Теорема Гаусса

Обратите внимание на математическую формулировку теоремы и ее физический смысл.

5 Дифференциальная форма т Гаусса
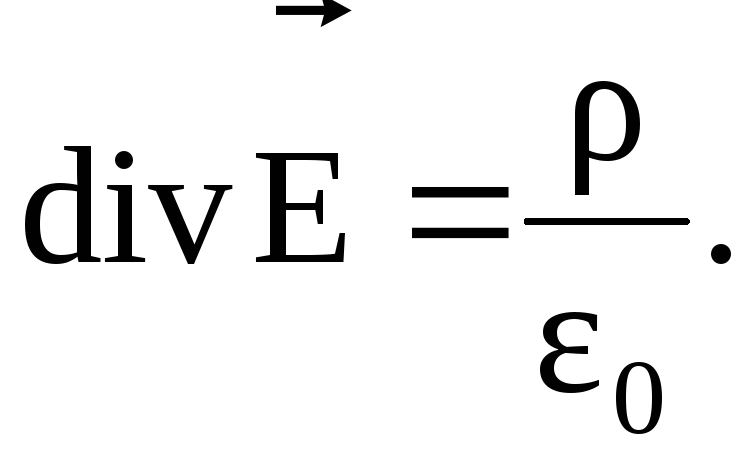

Практикуйтесь в решении задач, связанных с применением теоремы Гаусса в интегральной форме.

Теорема гаусса (общее)

Используйте визуальные материалы, чтобы лучше понять геометрическое представление теоремы.

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.

Изучите примеры из электродинамики, где применяется теорема Гаусса.

Лекция 4-4 Теорема Гаусса в дифференциальной форме

Посетите онлайн-курсы или лекции, посвященные векторному анализу и теореме Гаусса.

Работайте в группах с другими студентами или коллегами для обмена знаниями и идеями.

Билет №02 \


Часто проверяйте свои знания, решая задачи с использованием теоремы Гаусса.

Лекция 2.3. Теорема о циркуляции
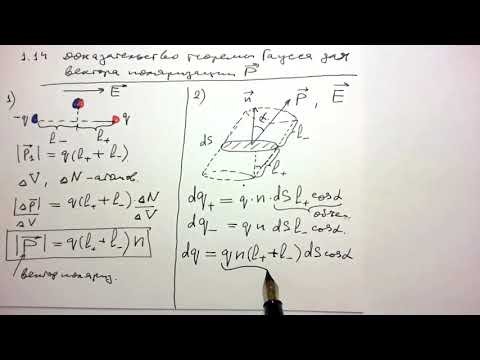
Лекция 4-5 Доказательство теоремы Гаусса для вектора поляризации

Используйте программное обеспечение для моделирования и визуализации полей и потоков.

Следите за новыми публикациями и исследованиями в области векторного анализа и его приложений.

Система уравнений Максвелла. Связь интегральной и дифференциальной формы уравнений.
