Теорема Ролля и ее геометрическое значение в математике
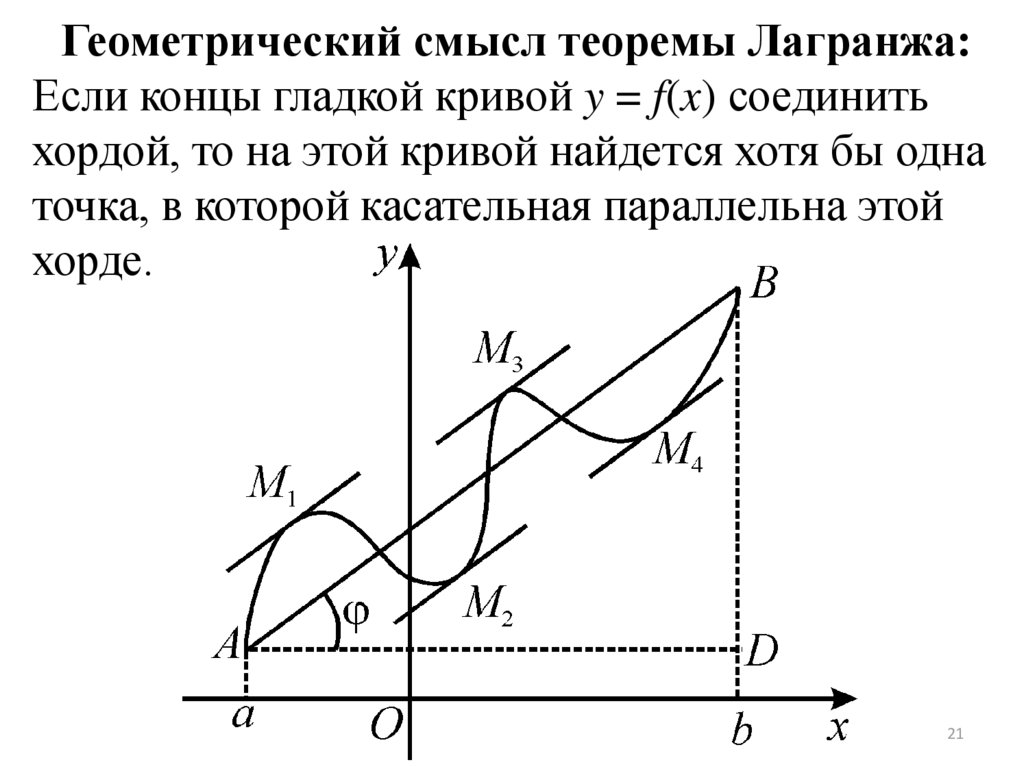
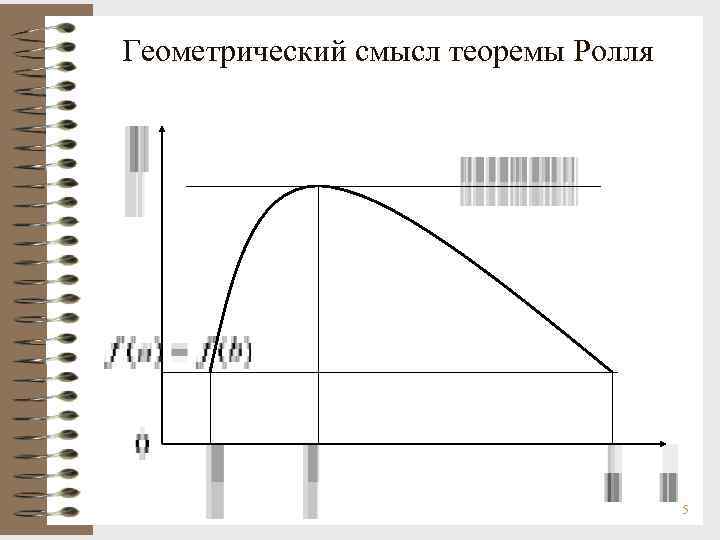
Теорема Ролля является важным результатом в анализе, который иллюстрирует связь между производными функции и геометрией ее графика. Поняв ее геометрический смысл, можно глубже понять поведение функций и их критические точки.
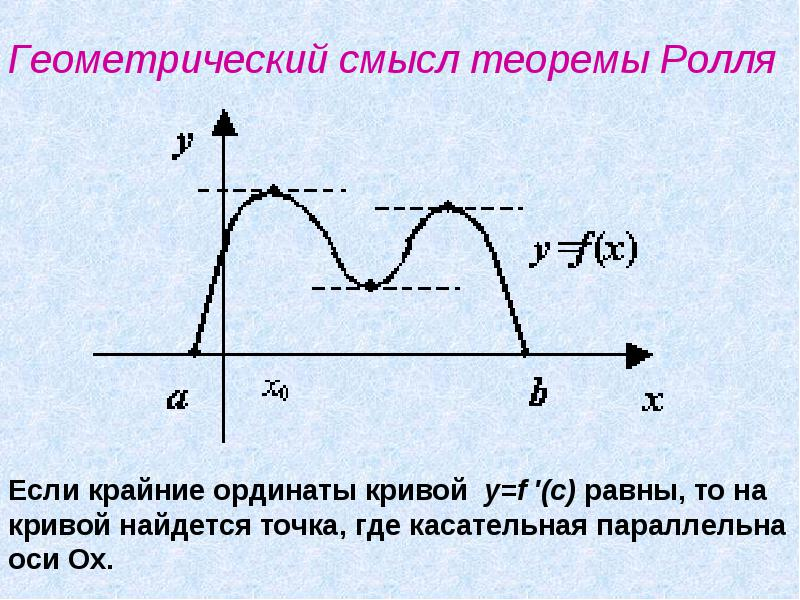

При изучении теоремы Ролля важно визуализировать график функции, чтобы увидеть, где касательная горизонтальна.

Высшая математика. Теорема Ферма, Ролля, Лагранжа, Коши

Используйте графические калькуляторы или программное обеспечение для построения графиков, чтобы лучше понять геометрический смысл теоремы Ролля.

Теорема Ролля / доказательство простыми словами

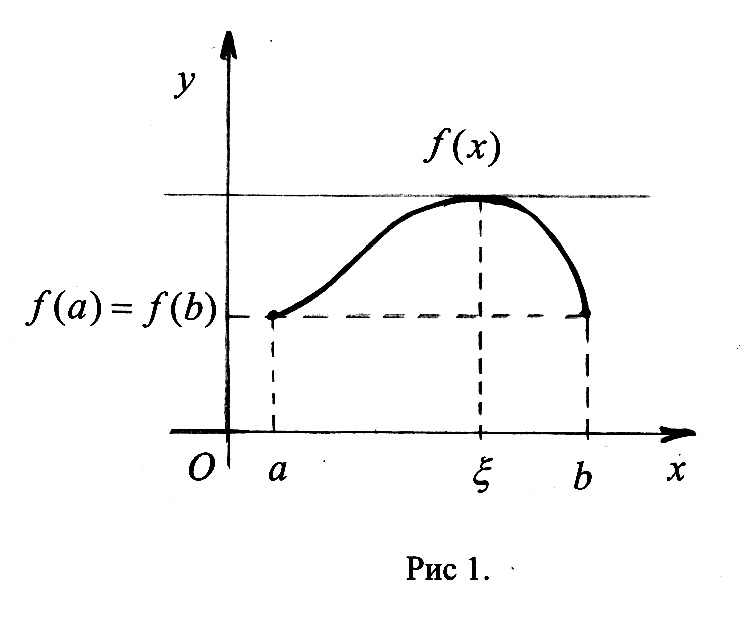
Обратите внимание на условия теоремы: функция должна быть непрерывной на отрезке и дифференцируемой на его интерьере.

Топология. Отражение гипотезы Пуанкаре на 3D моделях.


Понимание примеров и контрпримеров поможет лучше усвоить теорему Ролля и избежать типичных ошибок.

Теорема Лагранжа / простыми словами
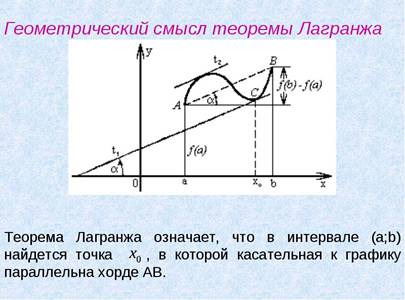
Практикуйтесь на различных функциях, чтобы увидеть, как теорема Ролля применяется в разных ситуациях.

Теорема Ролля, Коши, Лагранжа

Изучайте исторический контекст и развитие теоремы, чтобы оценить ее значимость в математике.

Матан. Теорема Ролля - bezbotvy
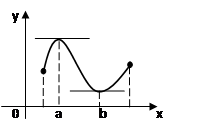
Связывайте теорему Ролля с другими теоремами, такими как теорема Лагранжа, для более глубокого понимания анализа.
Используйте теорему Ролля для проверки гипотез о поведении функций на заданных интервалах.
Практикуйте нахождение критических точек функции, чтобы понять, как теорема Ролля помогает в этом процессе.
Ищите дополнительные ресурсы, такие как видеолекции и статьи, для более глубокого изучения теоремы Ролля.
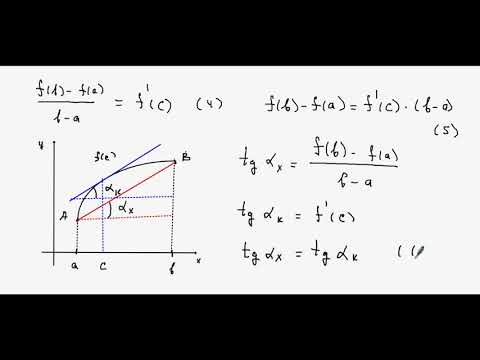
Теорема Лагранжа. Теорема Коши


Что доказал Григорий Перельман?