Исследование гиперболы и её уравнения: вторая степень кривизны
Гипербола является одной из конических кривых, определяемой уравнением второго порядка. На этой странице вы найдете фотографии, иллюстрирующие различные аспекты гиперболы, а также полезные советы по работе с её уравнением.

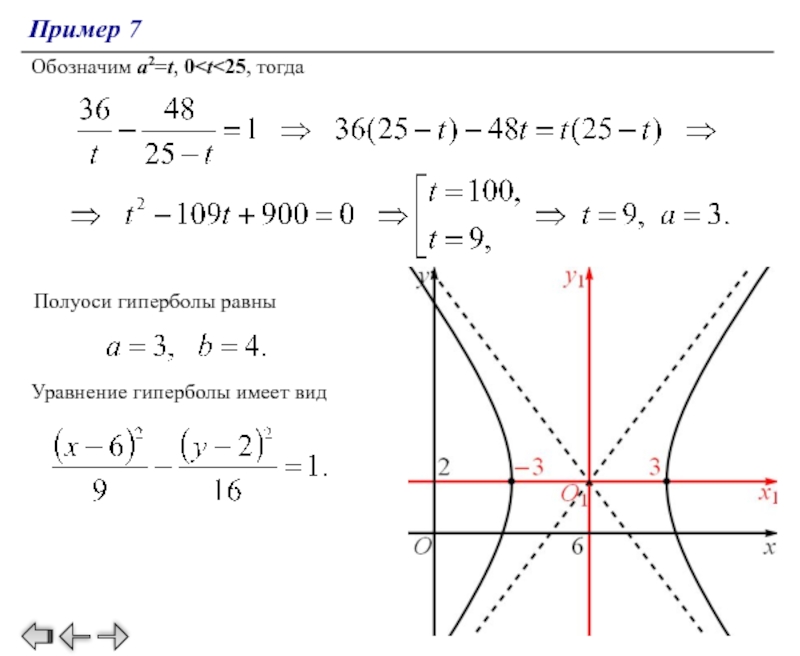
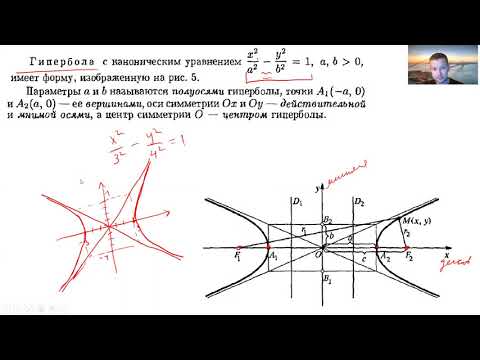
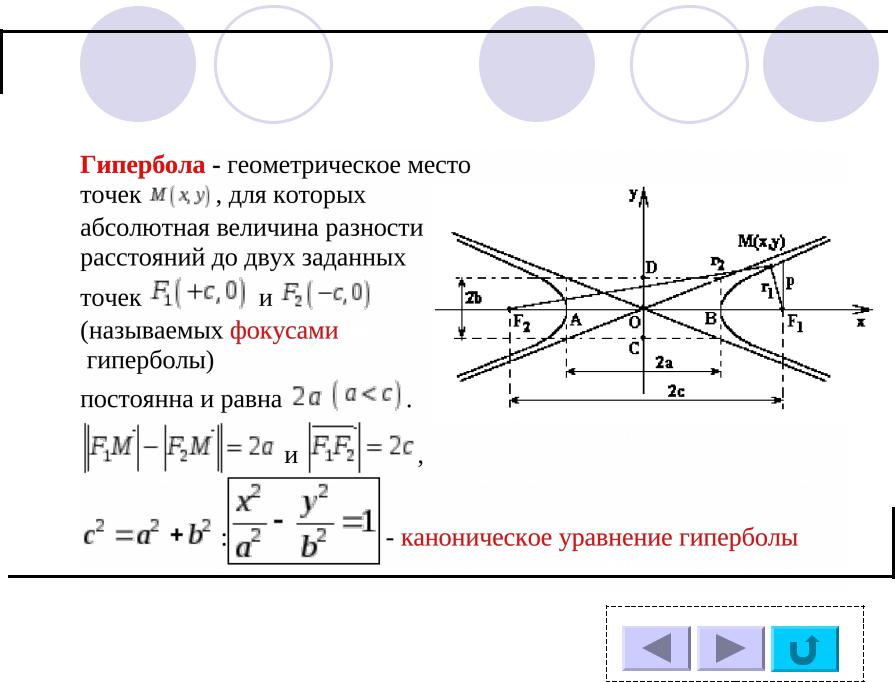
Начните изучение гиперболы с её основного уравнения: x²/a² - y²/b² = 1.

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертеж
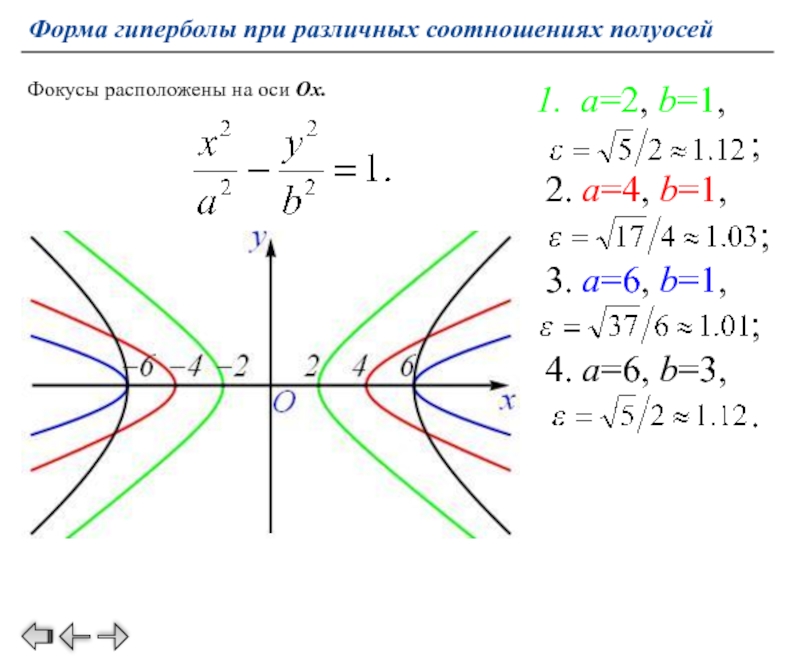
Помните, что гипербола имеет две ветви, которые расходятся в разные стороны.

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математика

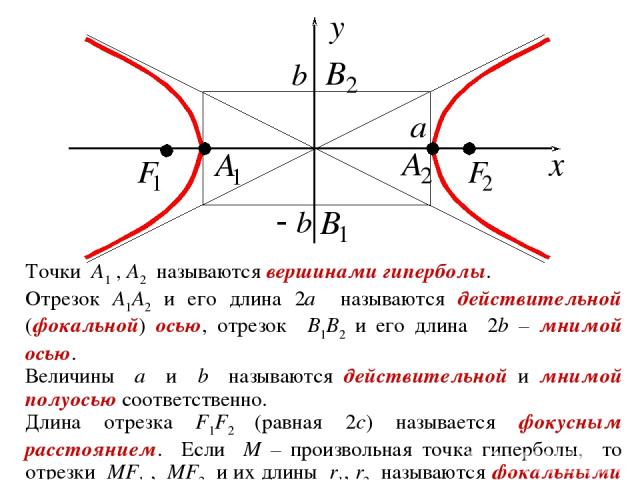
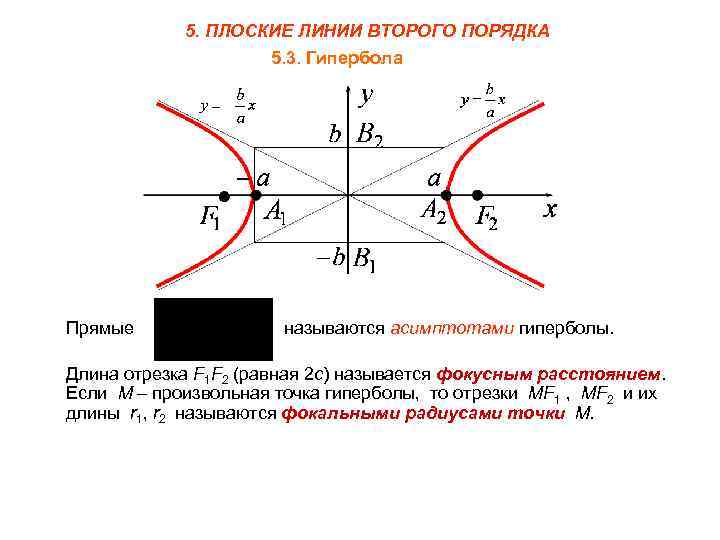
Фокусы гиперболы расположены на главной оси, и расстояние до них можно найти по формуле c² = a² + b².

Видеоурок \


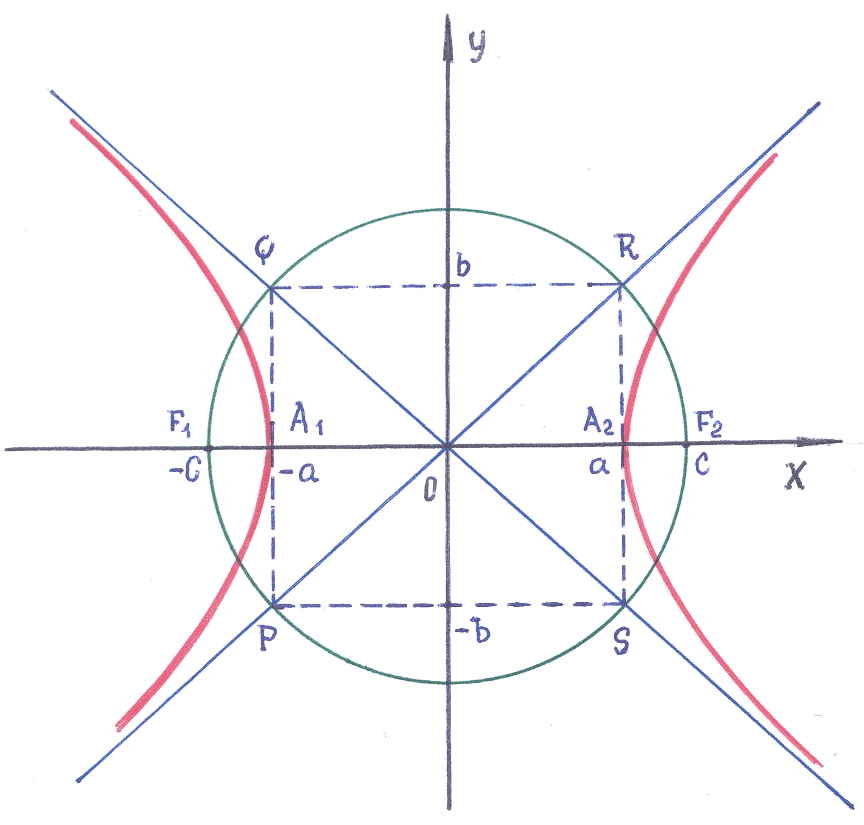
Ассимптоты гиперболы имеют уравнения y = ±(b/a)x, что помогает в построении её графика.
Математика без Ху%!ни. Кривые второго порядка. Эллипс.
Используйте графические калькуляторы для визуализации гипербол и проверки ваших расчетов.

Линал I Л5 Кривые второго порядка. Эллипс. Гипербола. Парабола
Практикуйтесь в преобразовании уравнений гиперболы к канонической форме.

Кривые второго порядка. Гипербола. Приведение к каноническому виду и чертеж

Обратите внимание на различия между гиперболами и другими коническими сечениями, такими как эллипсы и параболы.
Кривые второго порядка. Гипербола
Рассмотрите использование гипербол в реальных приложениях, таких как навигация и физика.

Лекция 31.1. Кривые второго порядка. Эллипс

Изучите влияние параметров a и b на форму и расположение гиперболы.

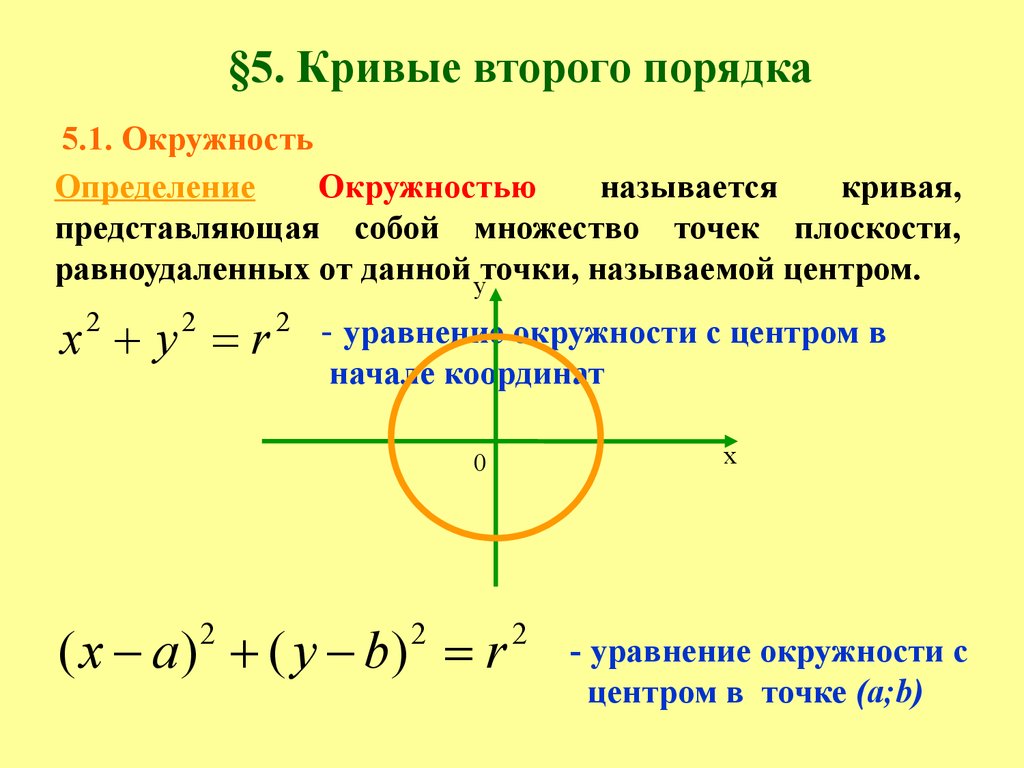
Кривые второго порядка

Помните, что гипербола симметрична относительно своих ассимптот и осей координат.

Лекция 31.2. Кривые второго порядка. Гипербола.

