Эффективные способы решения неоднородных дифференциальных уравнений
В данной статье рассматриваются различные методы и приемы для нахождения частных решений неоднородных дифференциальных уравнений. Приведены полезные советы и примеры для облегчения понимания и практического применения.



Перед началом решения убедитесь, что вы правильно определили тип уравнения и его неоднородную часть.
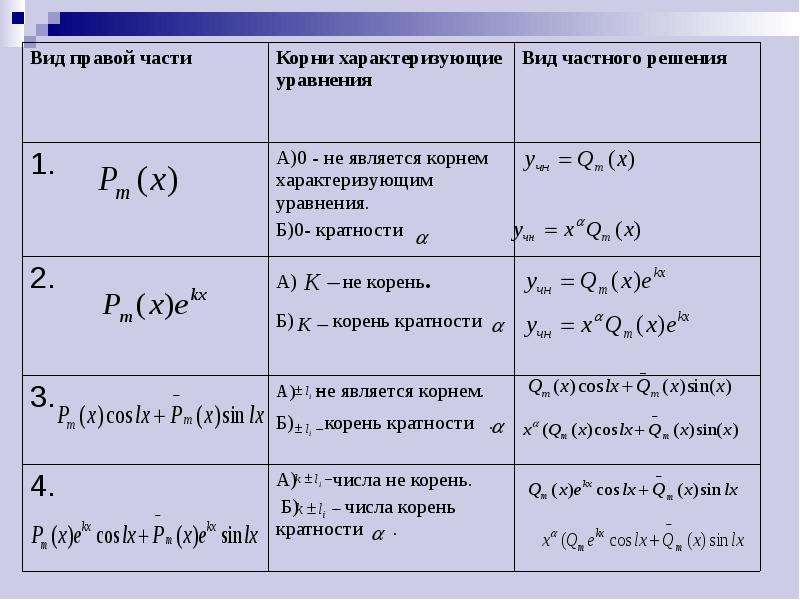
Нахождение вида частных решений ЛНДУ

Используйте метод подбора частного решения, подставляя предполагаемую форму решения в уравнение.

Математика без Ху%!ни. Линейные неоднородные дифференциальные уравнения 2 порядка.
Для линейных неоднородных уравнений с постоянными коэффициентами рассмотрите метод вариации постоянных.

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
Помните, что общее решение неоднородного уравнения состоит из частного решения и общего решения соответствующего однородного уравнения.

Математика без Ху%!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.

Для простоты расчетов можно использовать программное обеспечение, такое как Mathematica или MATLAB.

Чеголин А П Видео лекция \

Проверяйте свои решения, подставляя их обратно в исходное уравнение.

Изучите различные методы решения неоднородных уравнений, такие как метод неопределенных коэффициентов и метод интегрирующего множителя.
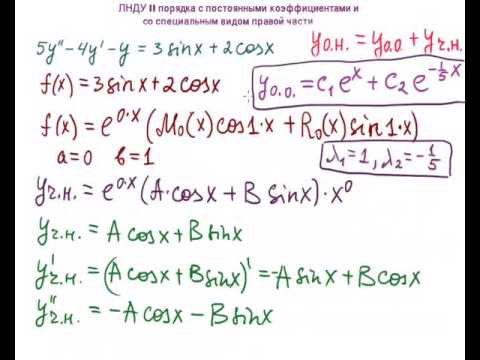
ЛНДУ II п. со спец. правой ч. (sin, cos)


Обратите внимание на граничные условия и особенности конкретной задачи, чтобы выбрать наиболее подходящий метод решения.

Регулярно практикуйтесь на различных примерах, чтобы укрепить понимание и навыки решения таких уравнений.

Не стесняйтесь обращаться за помощью к преподавателям или использовать онлайн-ресурсы для дополнительного обучения.


Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1