Способы вычисления второго катета в прямоугольном треугольнике
В этой статье мы рассмотрим различные методы нахождения второго катета в прямоугольном треугольнике. Вы узнаете, как использовать теорему Пифагора и тригонометрические функции для решения задач.


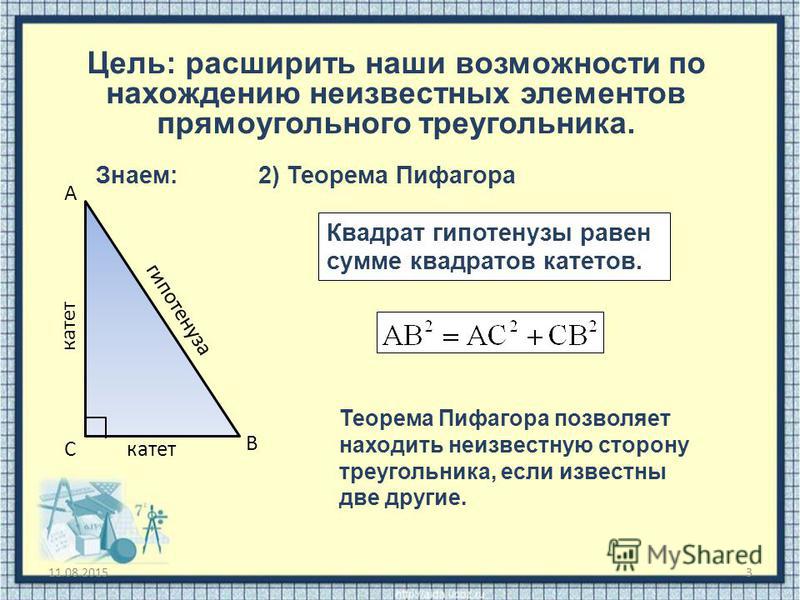
Для нахождения второго катета используйте теорему Пифагора: c2=a2+b2c^2 = a^2 + b^2c2=a2+b2, где ccc — гипотенуза, а aaa и bbb — катеты.
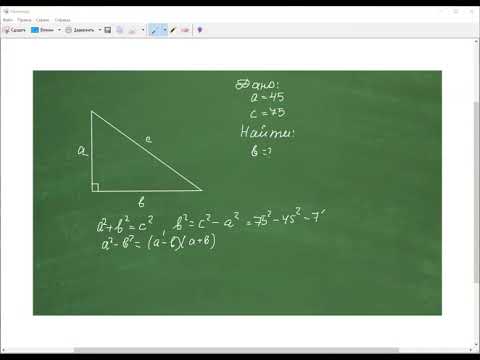
Лайфхак нахождения катета в прямоугольном треугольнике
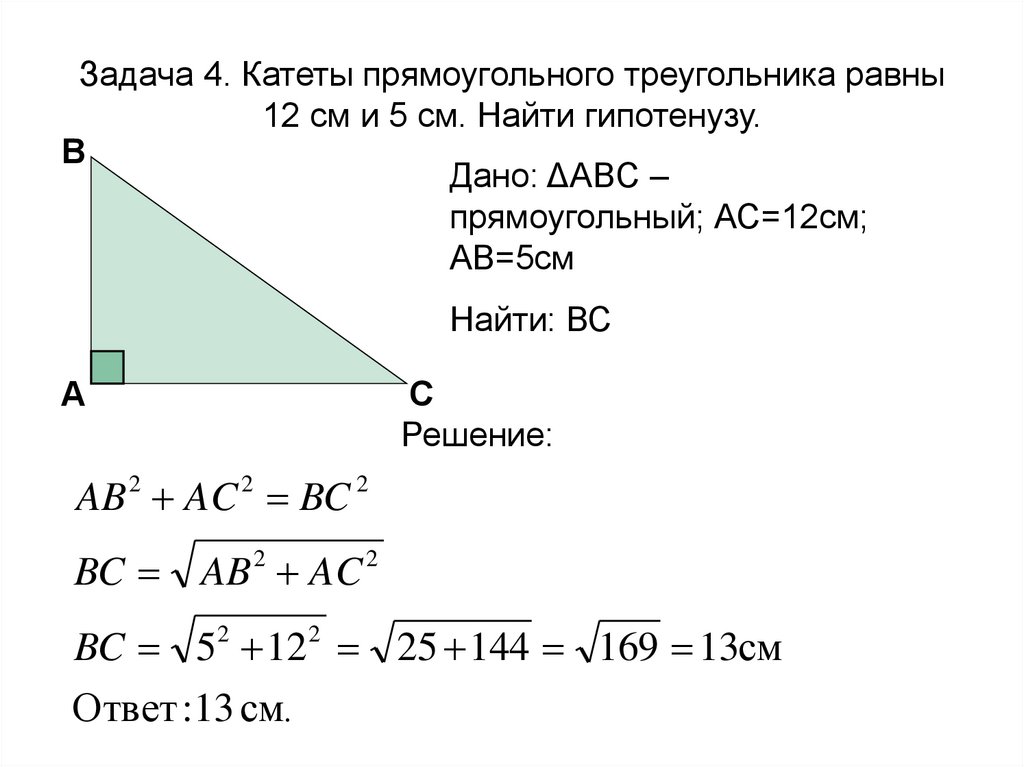
Если известен один катет и гипотенуза, второй катет можно найти по формуле: b=c2−a2b = /sqrt{c^2 - a^2}b=c2−a2.

Геометрия Один из катетов прямоугольного треугольника равен 21 см, а второй катет на 7 см меньше
В случаях, когда известны углы, используйте тригонометрические функции, такие как синус и косинус, для нахождения катетов.

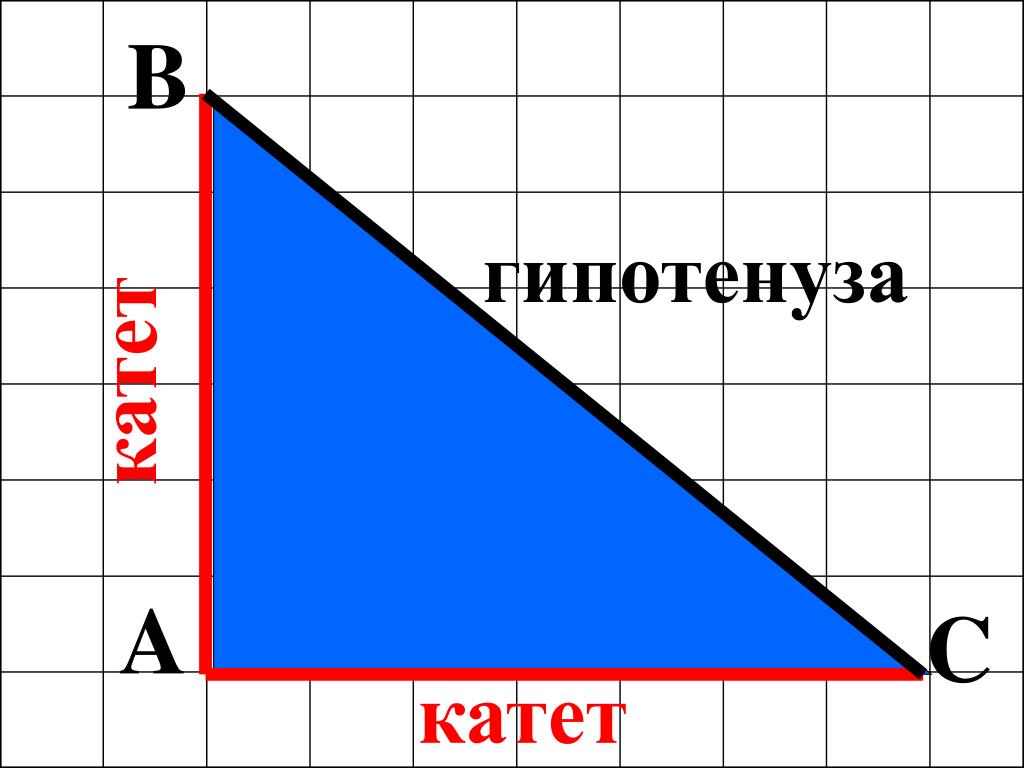
Катеты и гипотенуза

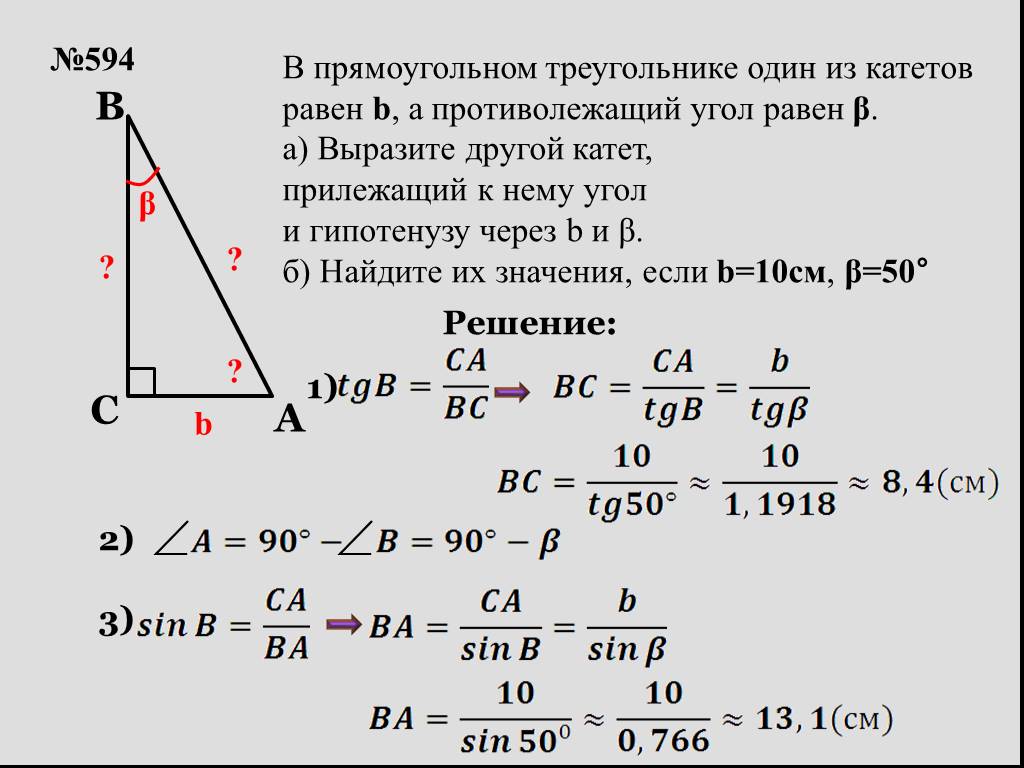
Синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе: sin(α)=ac/sin(/alpha) = /frac{a}{c}sin(α)=ca.

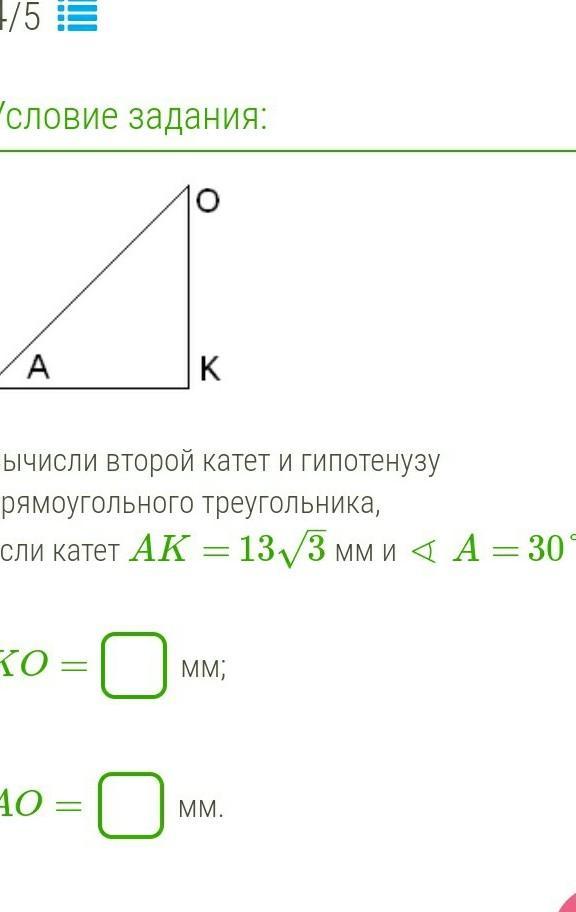
Классный способ для разметки любого угла без транспортира.
Косинус угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе: cos(α)=bc/cos(/alpha) = /frac{b}{c}cos(α)=cb.

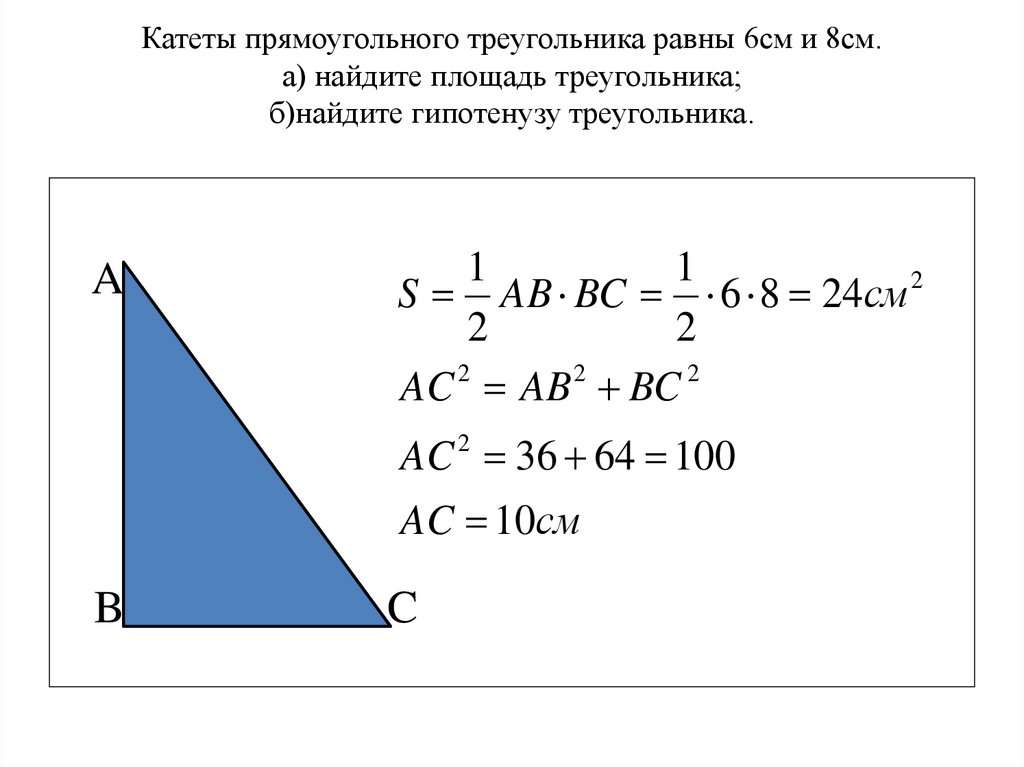
1710 два катета прямоугольного треугольника равны 8 и 7 найдите площадь этого треугольника
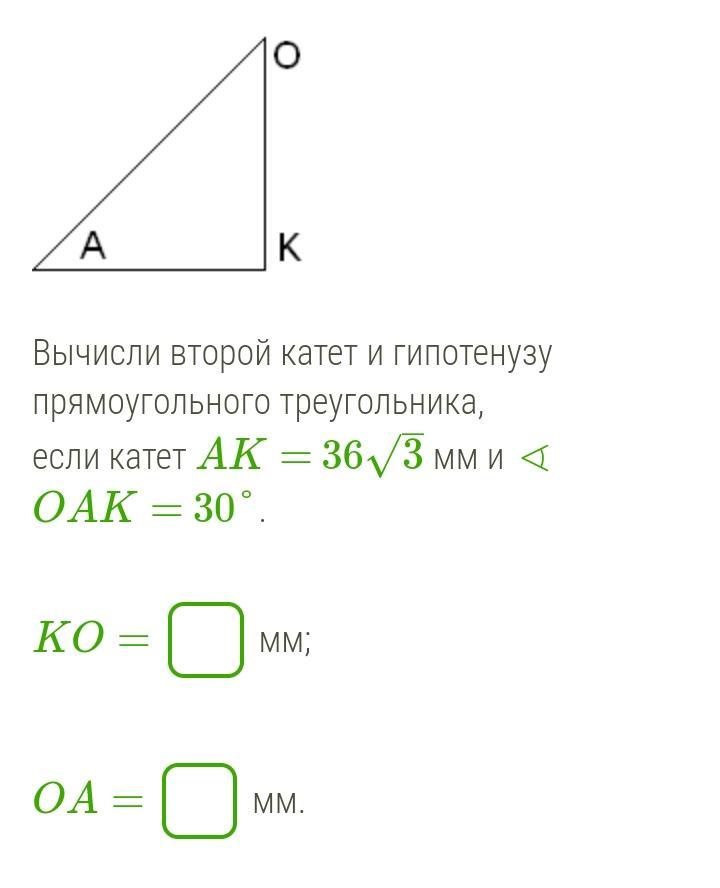
Тангенс угла равен отношению противолежащего катета к прилежащему: tan(α)=ab/tan(/alpha) = /frac{a}{b}tan(α)=ba.

Теорема Пифагора для чайников)))
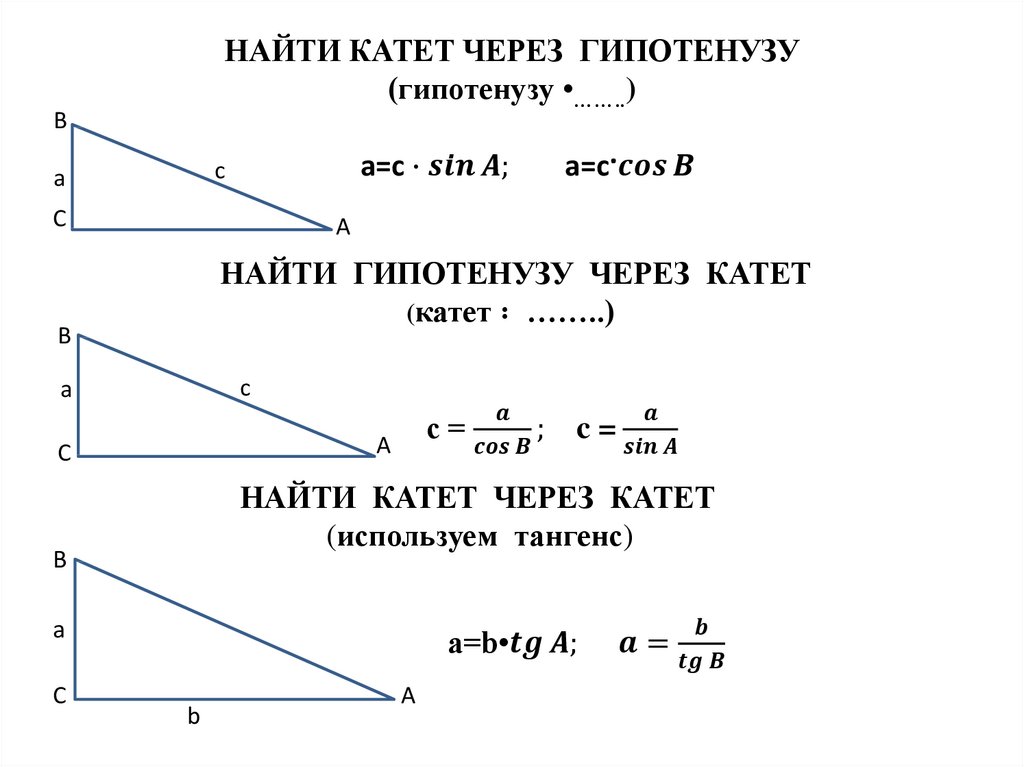
Если известен один катет и прилежащий угол, второй катет можно найти по формуле: a=b⋅tan(α)a = b /cdot /tan(/alpha)a=b⋅tan(α).

Для нахождения катета по синусу используйте формулу: a=c⋅sin(α)a = c /cdot /sin(/alpha)a=c⋅sin(α).
Для нахождения катета по косинусу используйте формулу: b=c⋅cos(α)b = c /cdot /cos(/alpha)b=c⋅cos(α).
Если нужно найти катет в прямоугольном треугольнике на координатной плоскости, используйте расстояние между точками: (x2−x1)2+(y2−y1)2/sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}(x2−x1)2+(y2−y1)2.

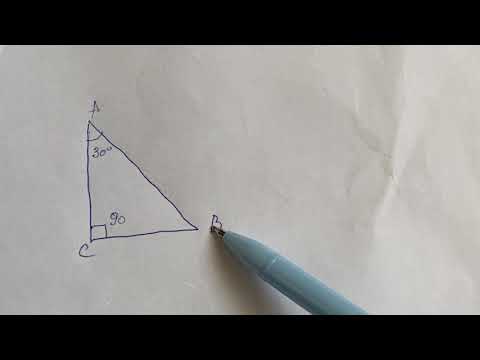
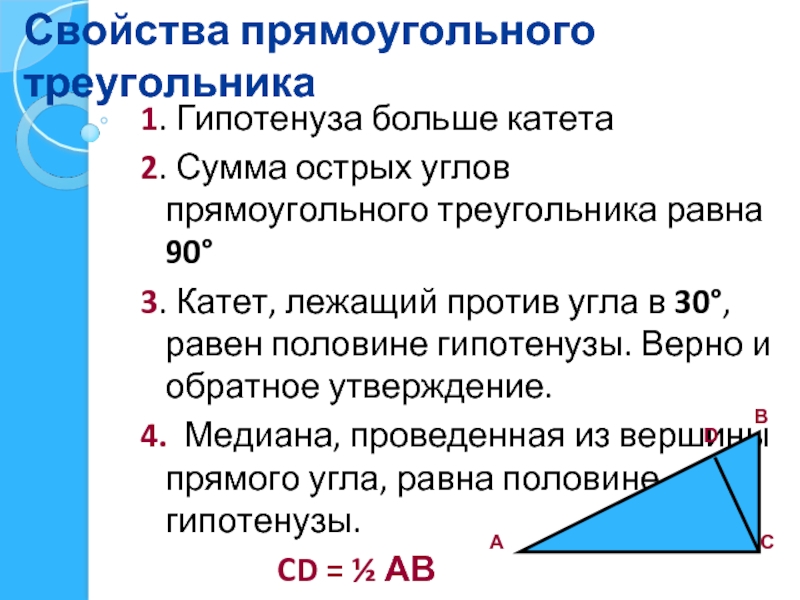
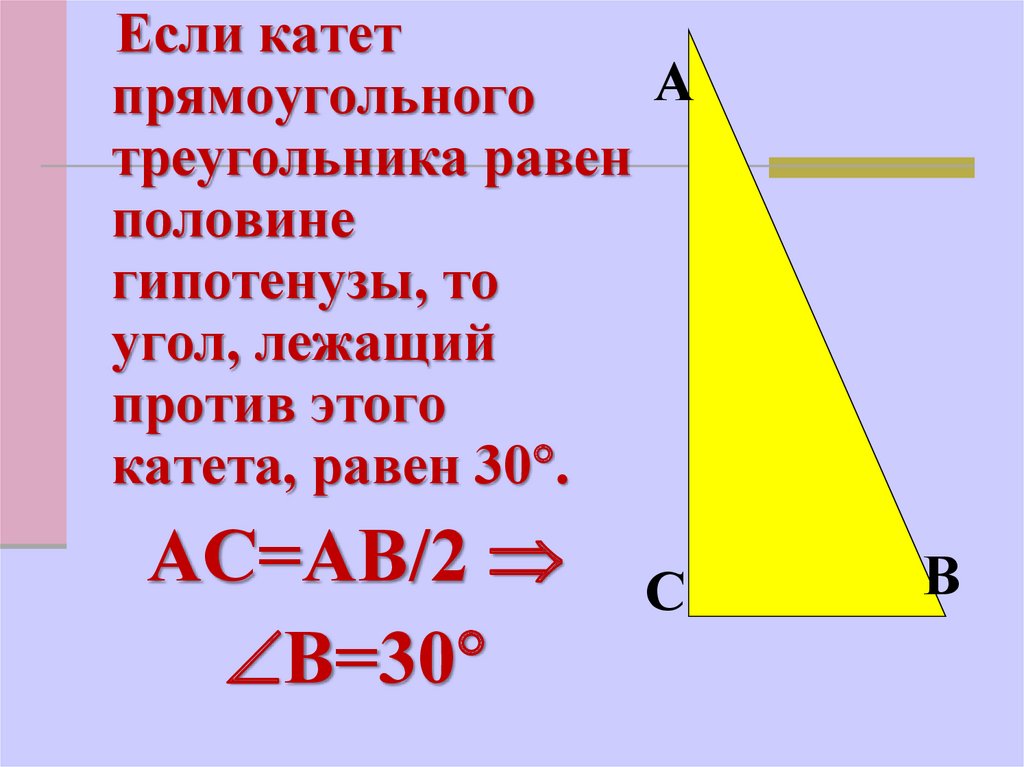
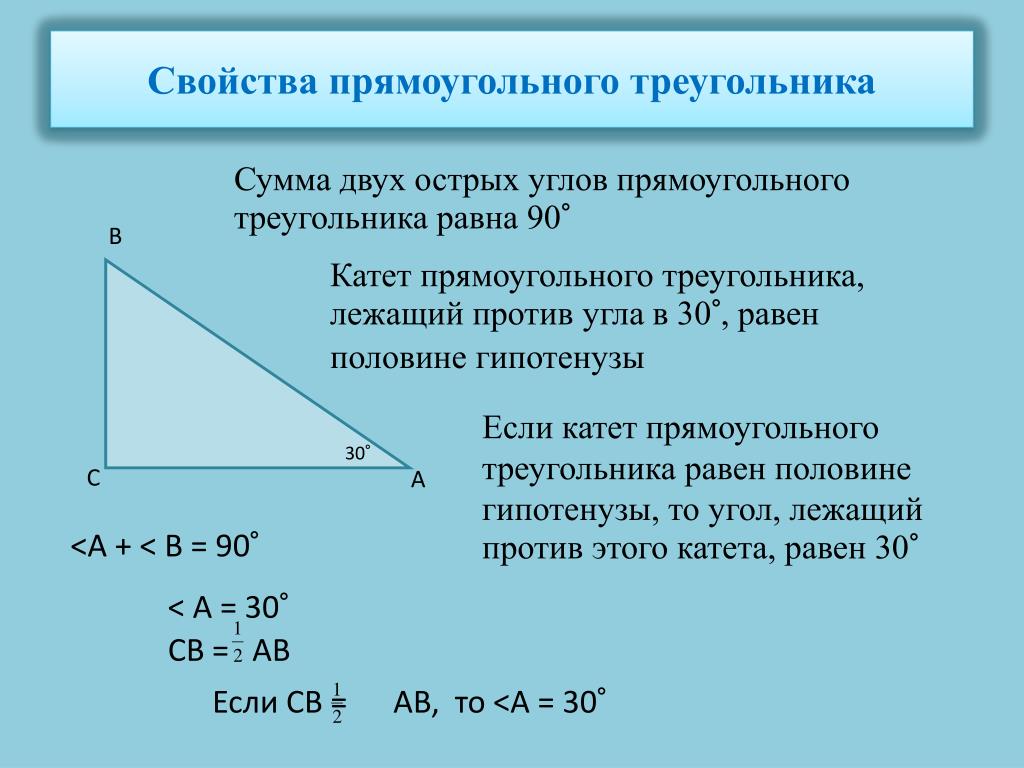
7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»