Методы доказательства подобия треугольников: пошаговые советы
На этой странице вы найдете подборку фотографий и полезные советы по доказательству подобия треугольников, изображенных на рисунке. Мы предлагаем пошаговое руководство и различные методы для доказательства.
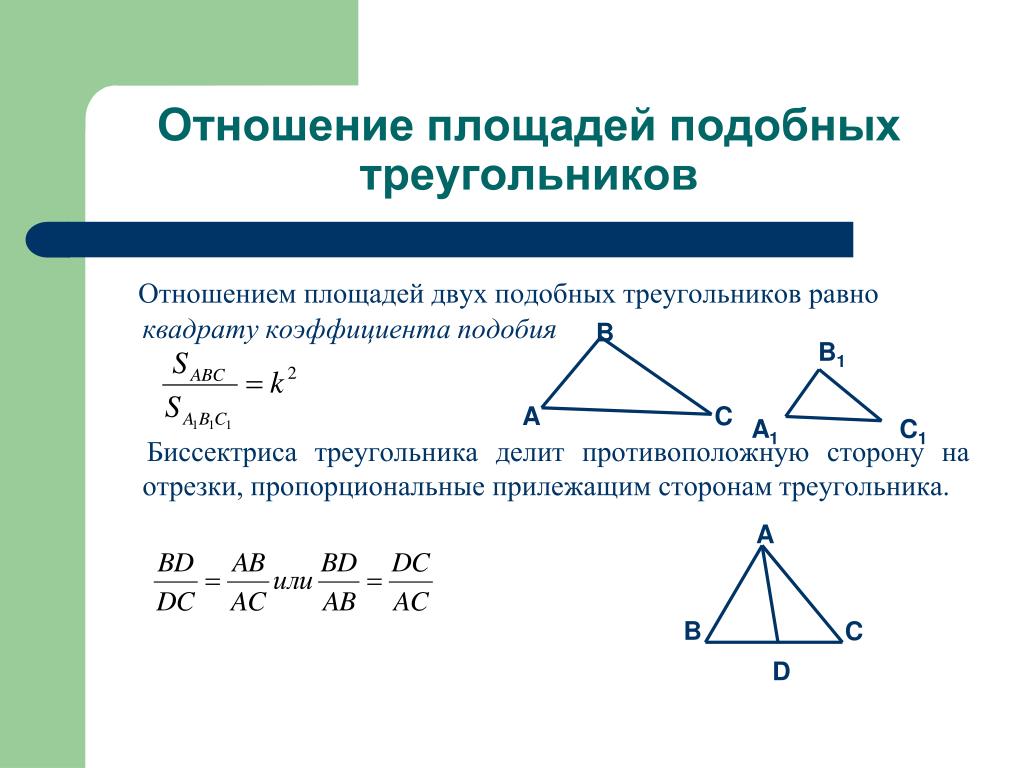
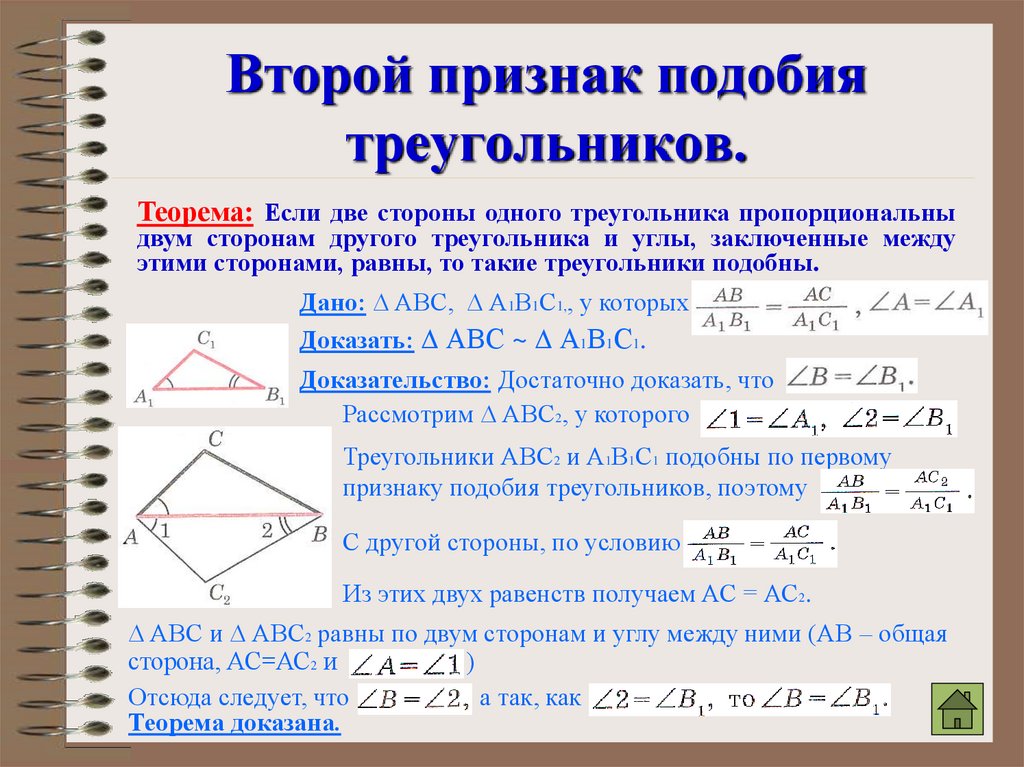

Используйте признак равенства углов для доказательства подобия треугольников.

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ коэффициент подобия 8 класс

Проверьте соотношение сторон двух треугольников: если оно одинаковое, треугольники подобны.

Подобие треугольников. Вся тема за 9 минут - ОГЭ по математике - Молодой Репетитор
Измерьте углы треугольников и сравните их. Если два угла одного треугольника равны двум углам другого, треугольники подобны.

Свойство биссектрисы треугольника с доказательством


Обратите внимание на признаки подобия треугольников: AA (два угла), SAS (сторона-угол-сторона) и SSS (три стороны).

Геометрия Укажите пары подобных треугольников, изображенных на рисунке, найдите длину отрезка x
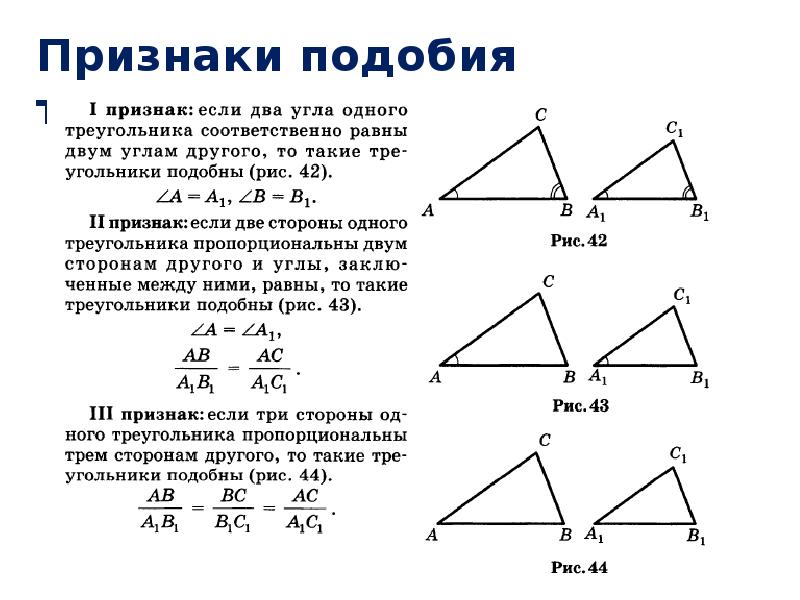
Используйте метод наложения: если один треугольник можно наложить на другой путем масштабирования, они подобны.

Геометрия Докажите, что в подобных треугольниках высоты, проведенные из вершины соответственных

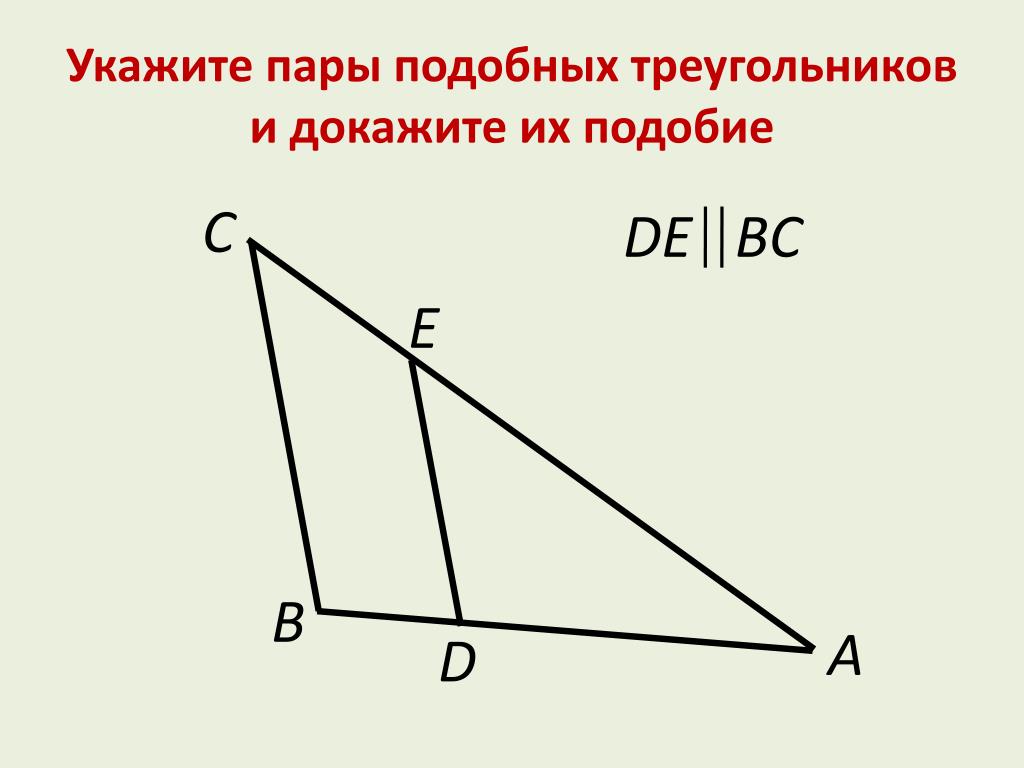
Проверьте параллельность сторон: если стороны одного треугольника параллельны сторонам другого, треугольники подобны.

ОГЭ Задание 25. Задача по геометрии на доказательство. Подобные треугольники.
Используйте теорему о средней линии: если в одном треугольнике проведена средняя линия, параллельная одной из его сторон, она делит треугольник на два подобных треугольника.

Примените теорему о биссектрисе угла: если биссектриса угла делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам, треугольники подобны.
Используйте пропорциональность сторон и углов в подобных треугольниках для доказательства их подобия.

Первый признак подобия треугольников. Доказательство. 8 класс.

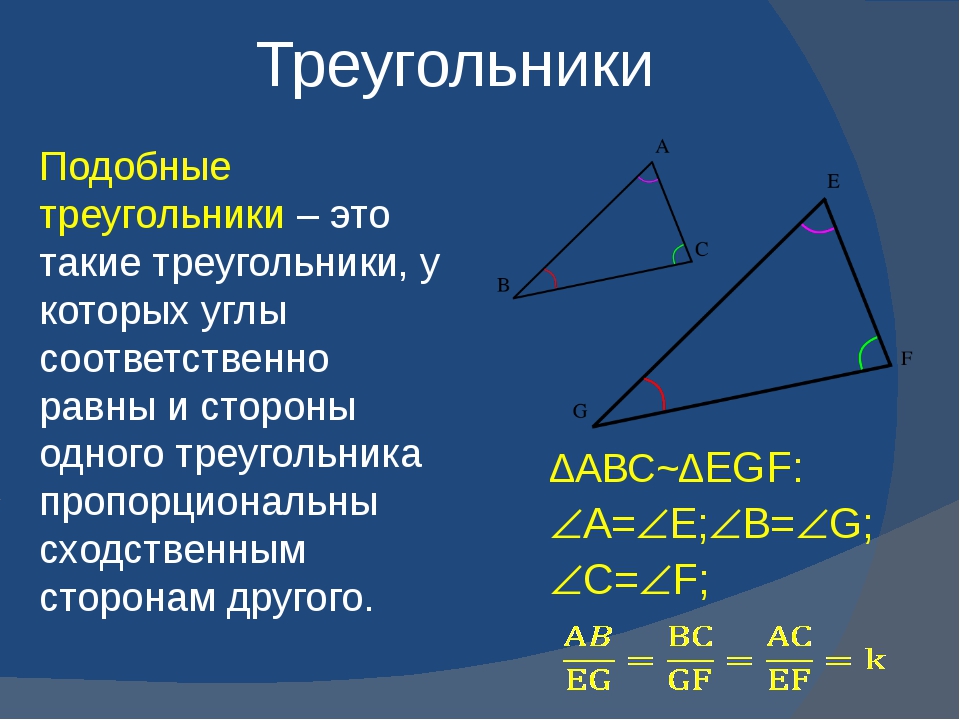
Проверьте, сохраняются ли углы и стороны при изменении масштаба одного из треугольников: если да, треугольники подобны.
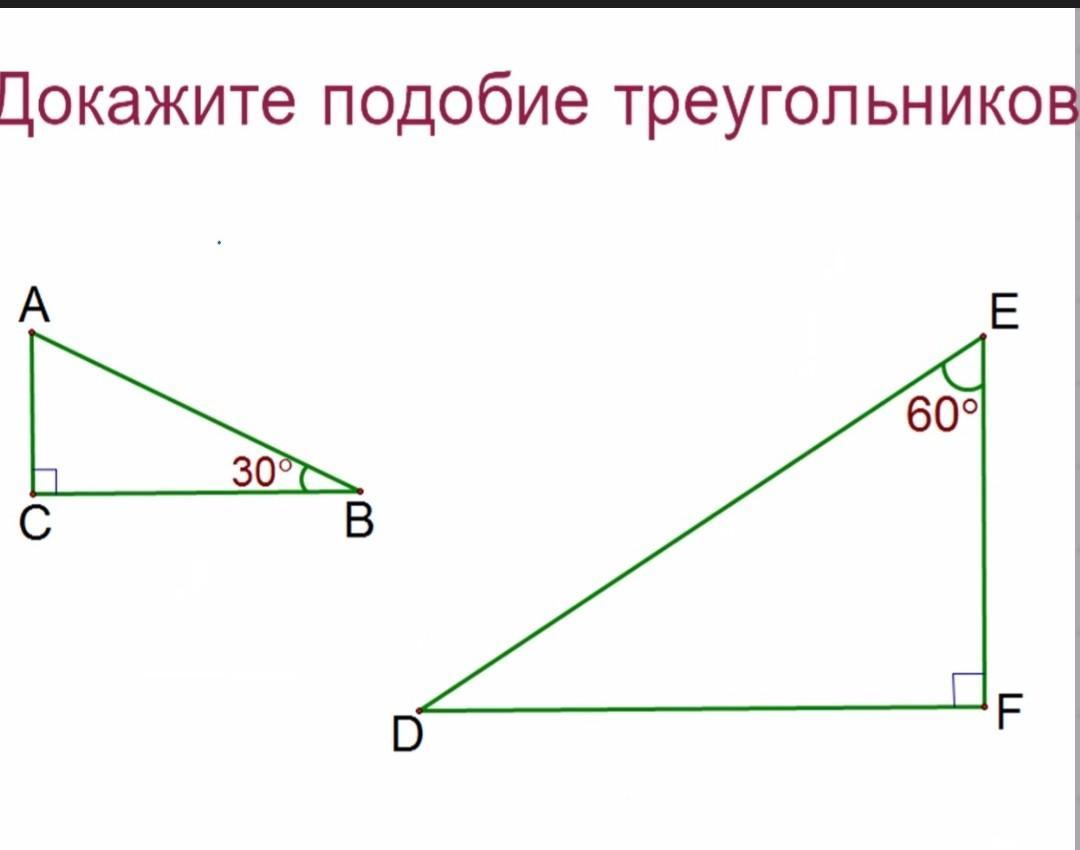

Подобие треугольников. Признаки подобия треугольников (часть 1) - Математика