Как использовать формулу полного квадратного уравнения: полное руководство
На этой странице вы найдете полное руководство по формуле полного квадратного уравнения. Узнайте, как применять эту важную математическую формулу для решения квадратных уравнений, а также получите полезные советы, которые помогут вам лучше понять и использовать эту формулу в практике.


Запомните, что полное квадратное уравнение имеет вид ax² + bx + c = 0, где a, b и c — коэффициенты, а x — переменная.
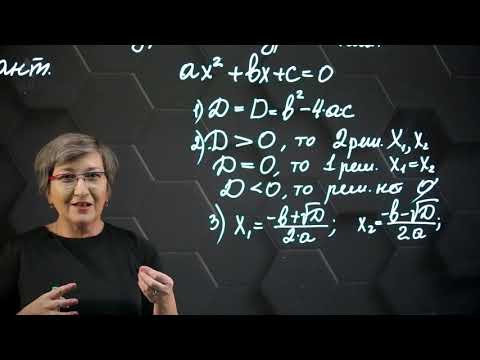
Решение квадратных уравнений. Дискриминант. 8 класс.
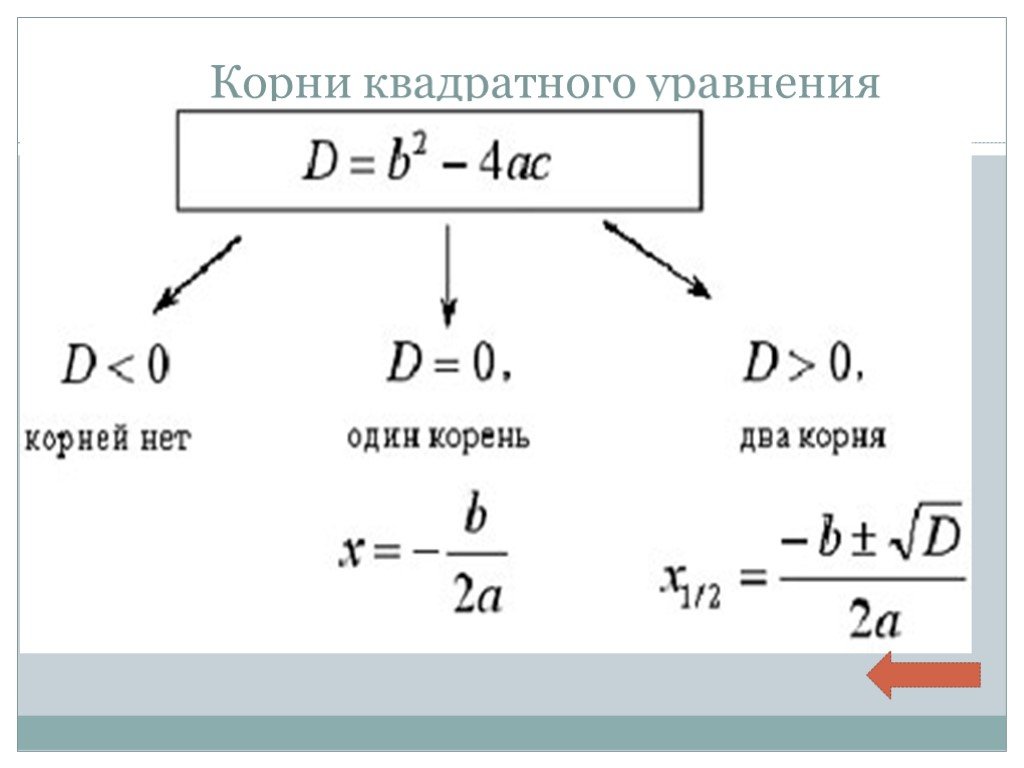
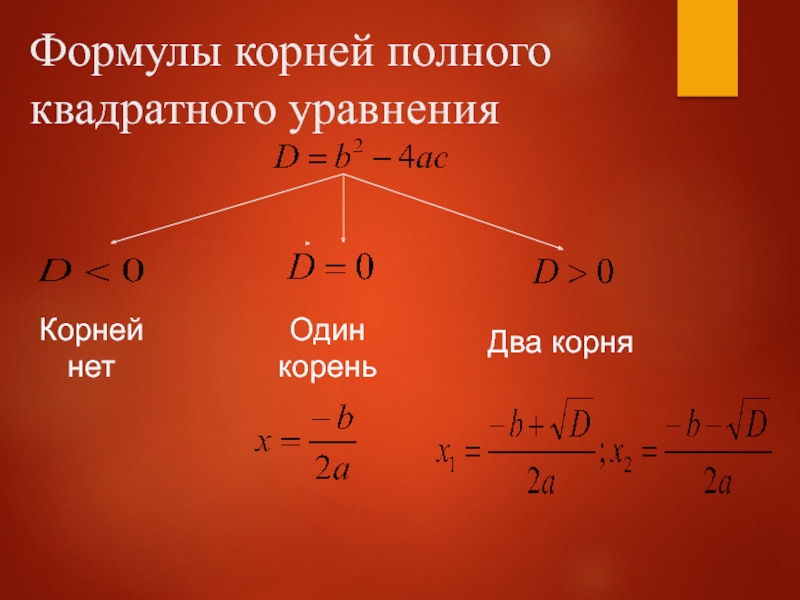
Для упрощения решения уравнения часто используют формулу дискриминанта: D = b² - 4ac. Это поможет определить количество и тип корней уравнения.

Решение квадратного уравнения с выводом формулы корней

Помните, что если дискриминант равен нулю, уравнение имеет один корень, а если положителен — два различных корня.

Формула корней квадратного уравнения (Доказательство)

В случае отрицательного дискриминанта уравнение не имеет действительных корней, а только комплексные.

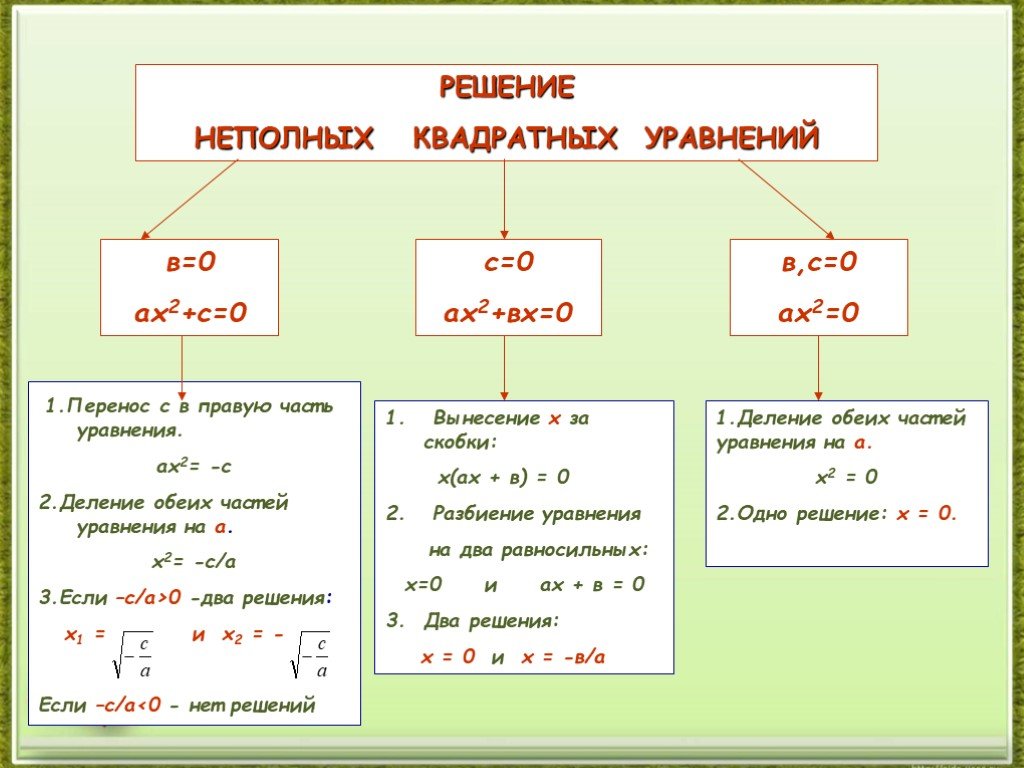
Как решать квадратные уравнения Решите уравнение 8 класс 9 класс Дискриминант Теорема Виета Формулы
Не забудьте про правило изменения знака при подстановке в формулу: x = (-b ± √D) / (2a).

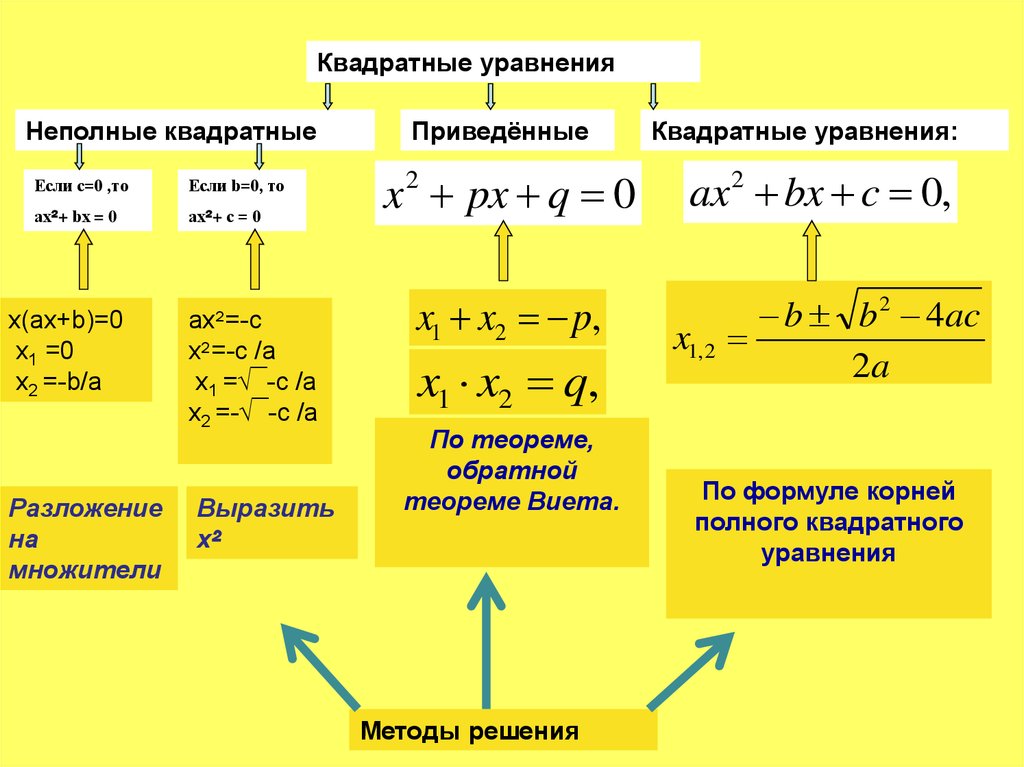
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?

Практикуйтесь на различных примерах, чтобы уверенно применять формулу в различных ситуациях.
Метод выделения полного квадрата. 8 класс.


Используйте графический метод для визуализации решений уравнения, это может помочь лучше понять процесс решения.

Записывайте промежуточные шаги, чтобы избежать ошибок при вычислениях.

Математик (2.2). Закон Мерфи - Максим Керн

Внимательно проверяйте все вычисления, особенно при работе с корнями и дробями.

Если вы сталкиваетесь с трудностями, не стесняйтесь обращаться к учебным пособиям или онлайн-ресурсам для дополнительной практики.

Формула корней квадратного уравнения. Алгебра, 8 класс

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета - Математика