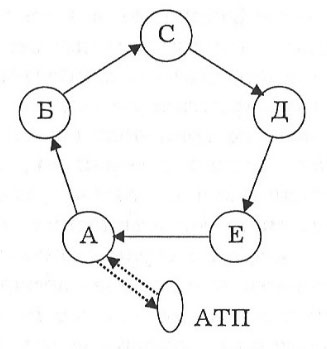
Эффективные кольцевые маршруты: советы по оптимизации транспортных задач
Кольцевые маршруты являются важной частью логистики, особенно в решении транспортных задач. Правильно составленный маршрут помогает сократить время в пути и оптимизировать использование ресурсов, что в итоге приводит к значительной экономии затрат и повышению эффективности. В этой статье мы рассмотрим, как составлять эффективные кольцевые маршруты, чтобы справиться с транспортной задачей наиболее рационально.
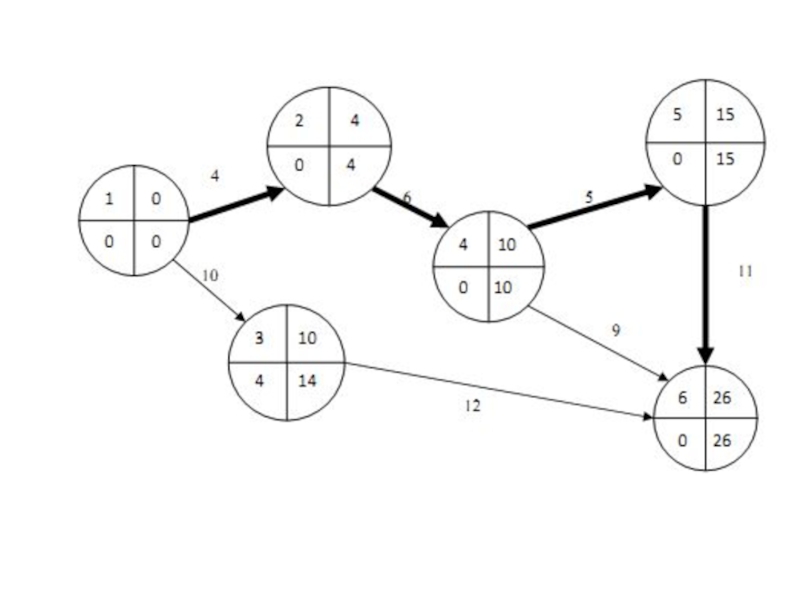

Анализируйте существующие маршруты, чтобы выявить наиболее эффективные пути и определить возможности для улучшения.

Лекция 5 Транспортная задача


Учитывайте время пиковых нагрузок, чтобы минимизировать задержки и улучшить скорость доставки.
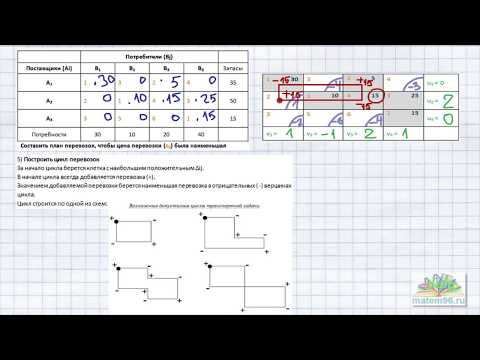
Транспортная задача (закрытая, с циклом). Метод потенциалов - подробно и понятно
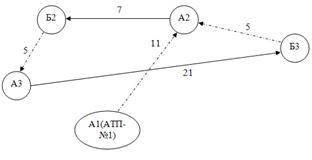
Используйте современные технологии, такие как GPS и системы управления транспортом, для точного мониторинга маршрутов.

Пример 1. Транспортная задача. Опорное решение. Метод северо-западного угла.
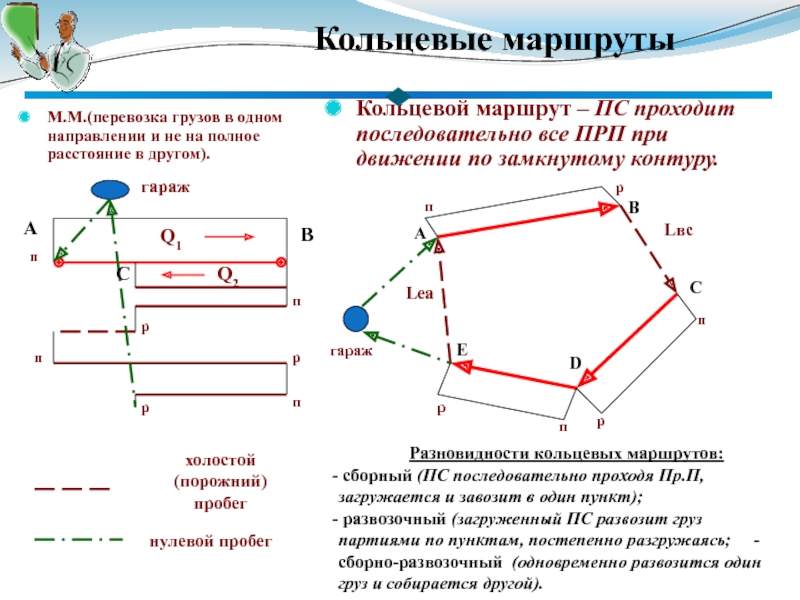
Разрабатывайте маршруты с учетом изменений в дорожных условиях и закрытия дорог, чтобы избежать непредвиденных задержек.
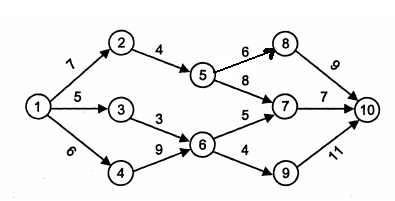
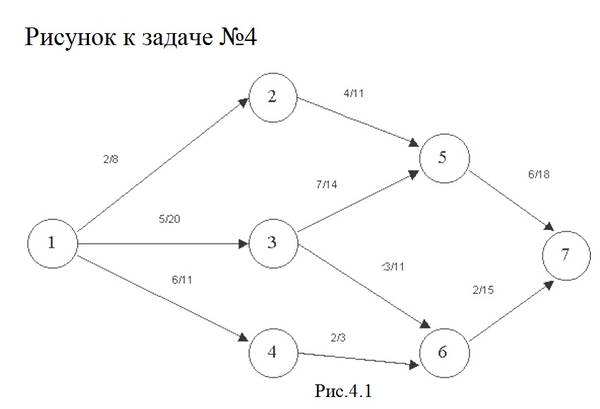
Транспортная задача
Старайтесь уменьшить количество пустых рейсов, планируя маршруты так, чтобы транспорт всегда был загружен по максимуму.

Транспортная задача для чайников по шагам за 15 минут. Применение транспортной задачи в экономике

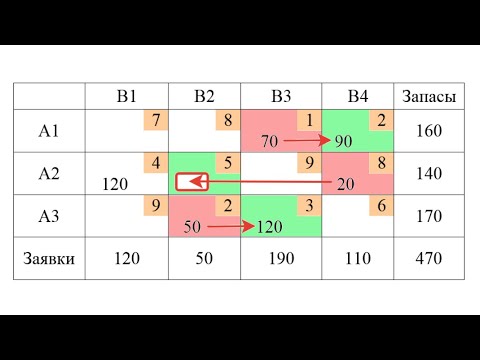
При планировании маршрута учитывайте возможные изменения в погодных условиях, которые могут повлиять на время в пути.

Транспортная задача
Планируйте регулярные остановки для технического обслуживания транспортных средств, чтобы предотвратить поломки на маршруте.

Метод ПОТЕНЦИАЛОВ. Транспортная задача
Обучайте водителей навыкам эффективного вождения, чтобы снизить затраты на топливо и увеличить безопасность на дорогах.
Решение транспортной задачи закрытого типа Поиском решений
Используйте математические модели и алгоритмы для оптимизации маршрутов и улучшения их эффективности.
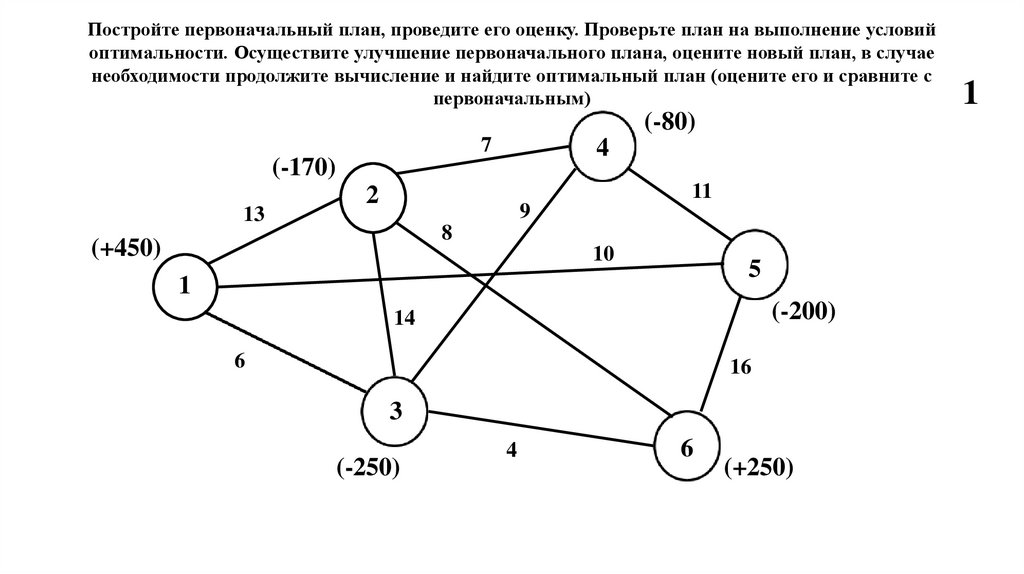

Всегда имейте резервный план на случай неожиданных обстоятельств, чтобы избежать задержек и дополнительных расходов.

Пример 1. Транспортная задача. Опорное решение. Метод минимального элемента.

Транспортная задача (открытая, без цикла). Метод потенциалов - подробно и понятно