Формулы и советы для вычисления косинуса угла в равнобедренном треугольнике
На этой странице вы найдете подборку фотографий и полезные советы по вычислению косинуса угла при вершине равнобедренного треугольника, а также необходимые формулы и примеры.
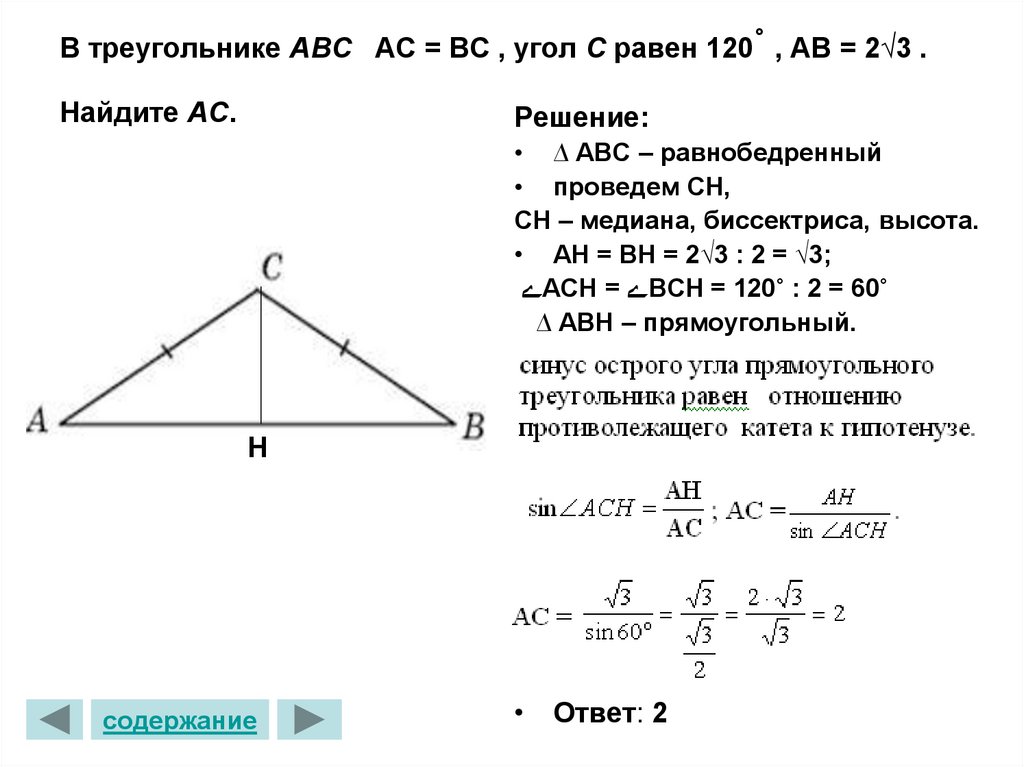
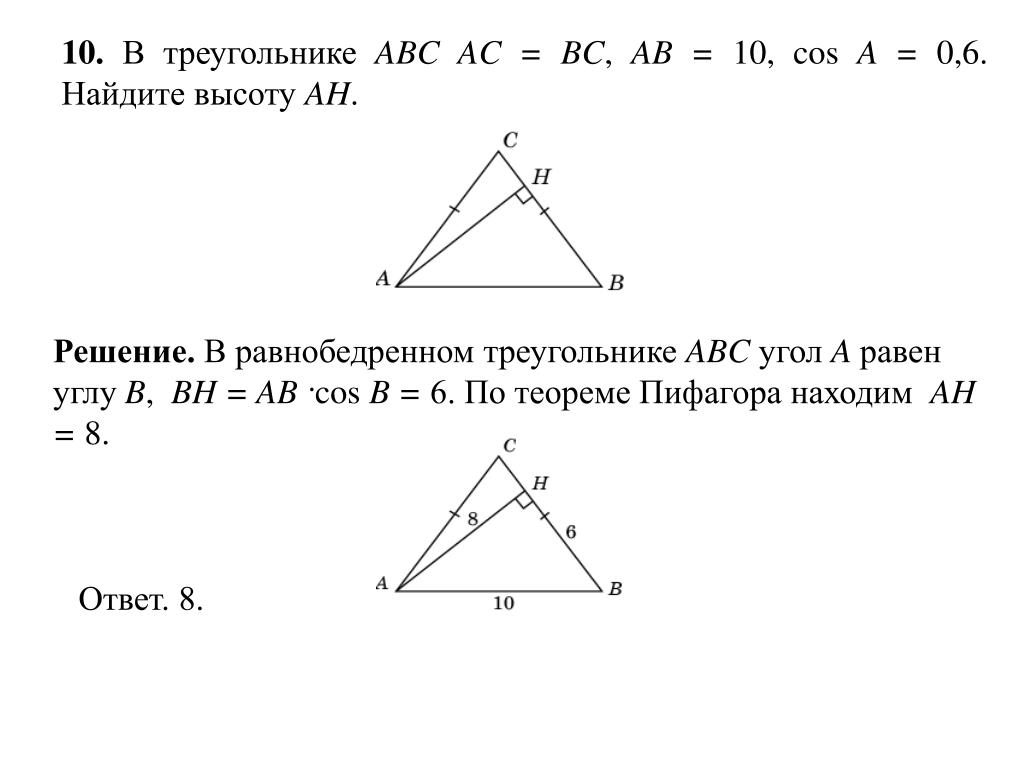
Используйте теорему косинусов для нахождения угла при вершине, если известны длины всех сторон треугольника.

1839 угол при вершине противолежащей основанию равнобедренного треугольника
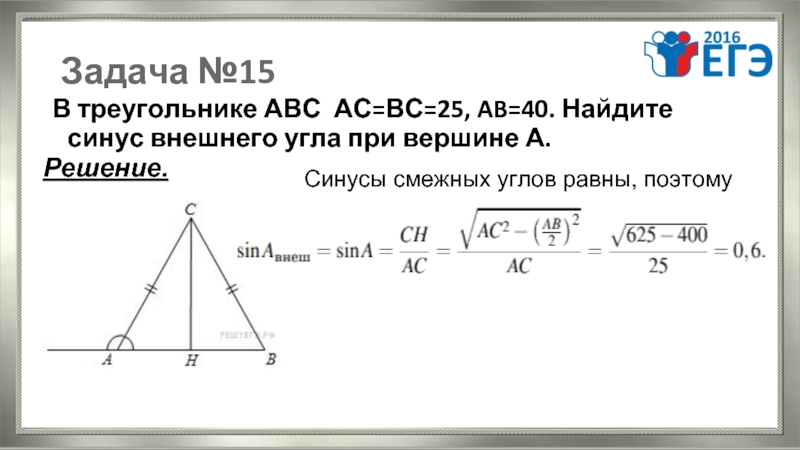
В равнобедренном треугольнике косинус угла при вершине можно найти через высоту, проведенную к основанию.

угол при вершине противолежащей основанию равнобедренного треугольника равен 150
Не забывайте, что углы при основании равнобедренного треугольника равны между собой.

Тригонометрия с нуля - Синус, косинус, тангенс и котангенс - Умскул - Средняя школа

Для нахождения косинуса угла при вершине можно использовать формулу: cos(α) = (a² + b² - c²) / (2ab), где a и b - боковые стороны, а c - основание треугольника.
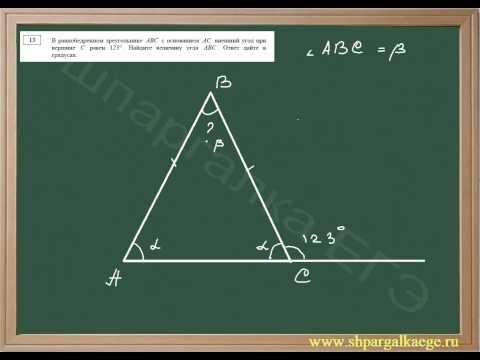
Определение угла равнобедренного треугольника

Высота, опущенная на основание равнобедренного треугольника, делит его на два равных прямоугольных треугольника.

Задача 6 №27900 ЕГЭ по математике. Урок 128
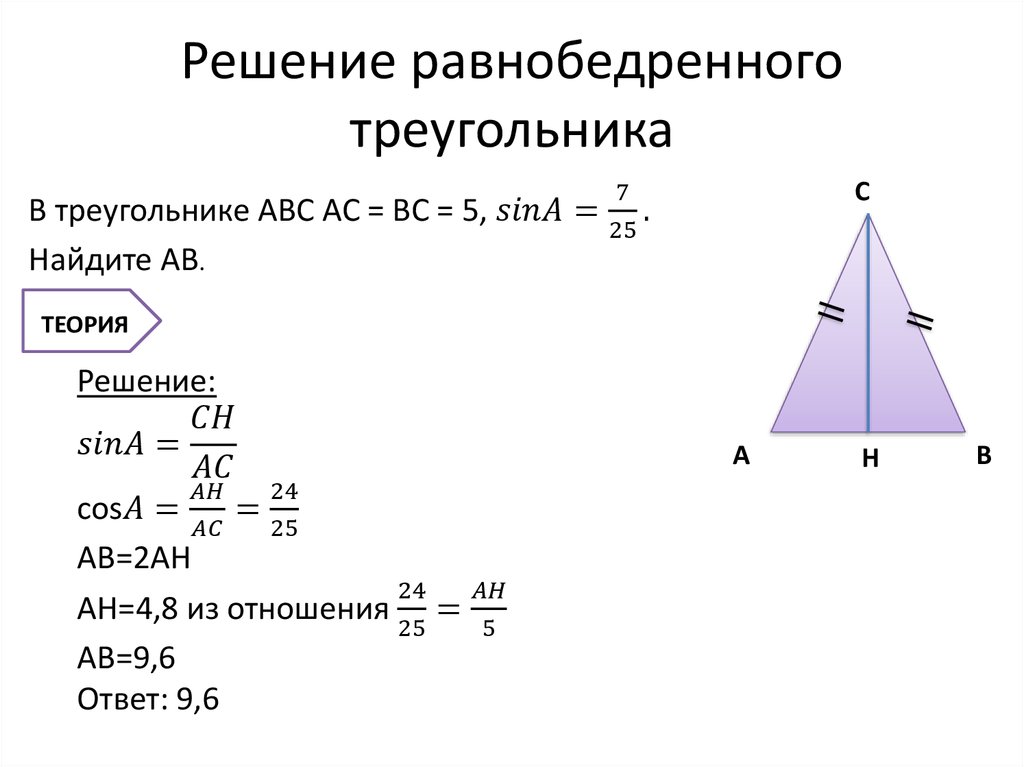
Для упрощения расчетов можно использовать специальные математические калькуляторы.

Геометрия Угол при вершине равнобедренного треугольника равен β, высота, проведенная к боковой

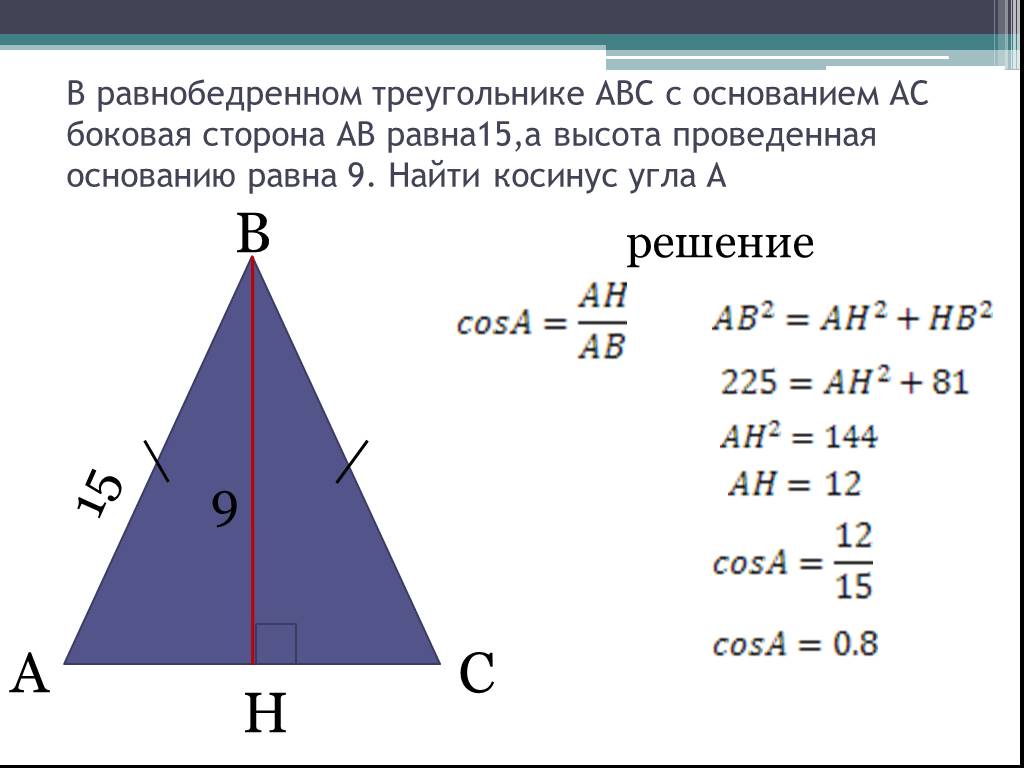
Проверяйте свои вычисления несколько раз, чтобы избежать ошибок.
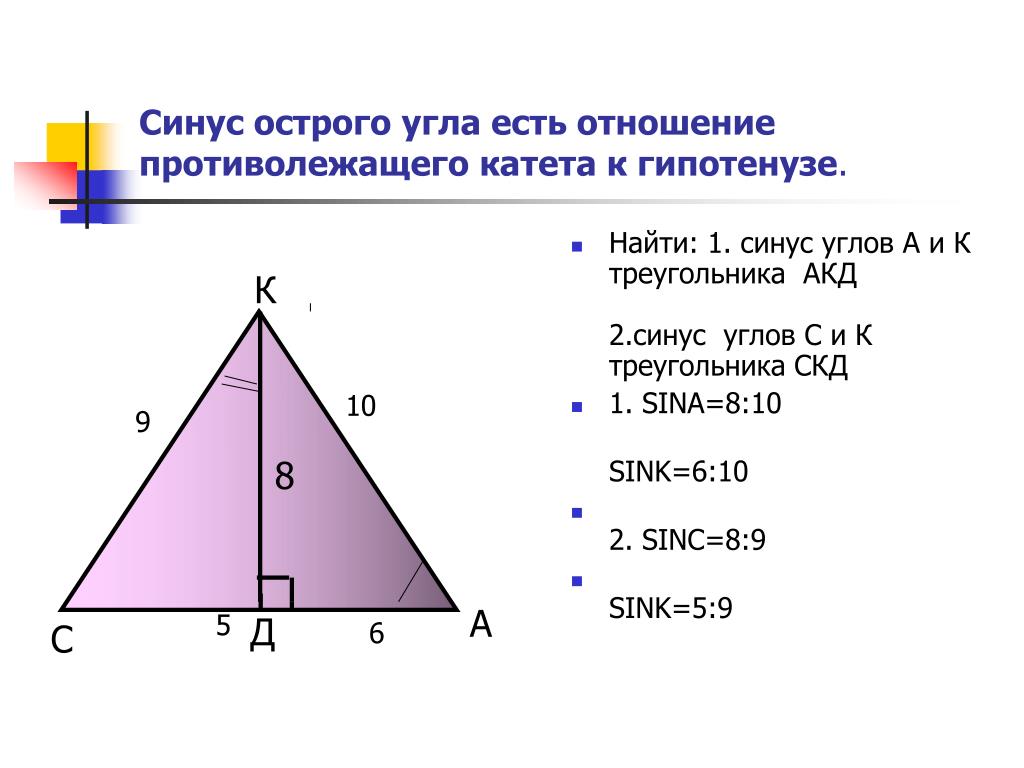
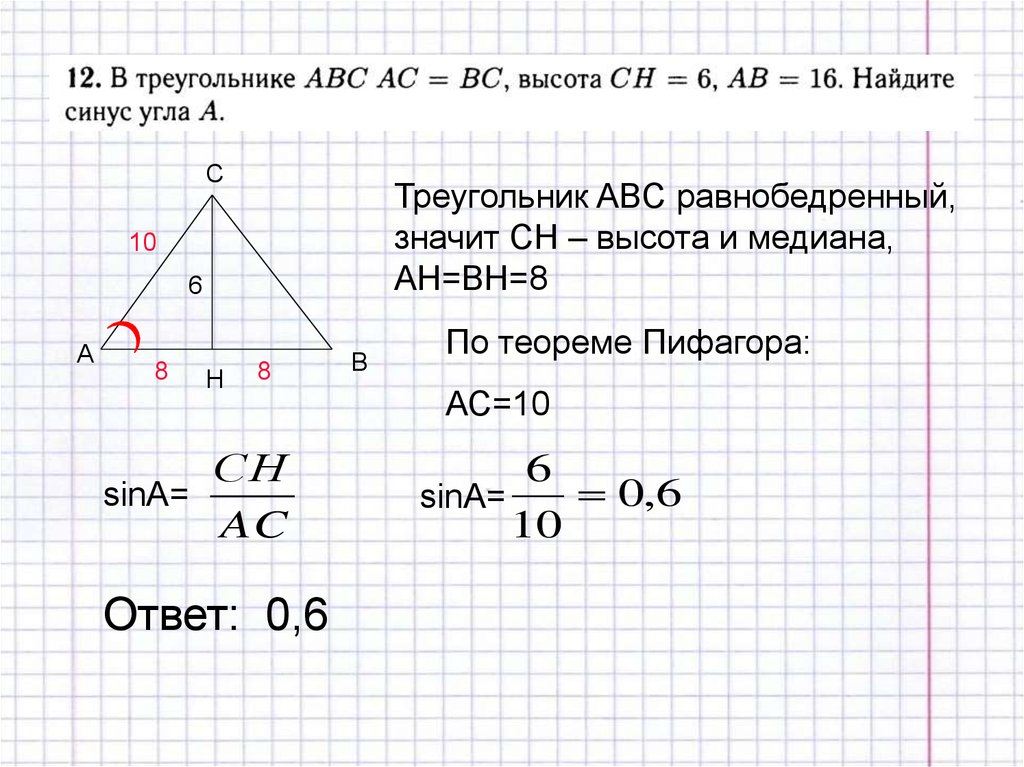
При решении задач на нахождение косинуса угла используйте наглядные рисунки и схемы.
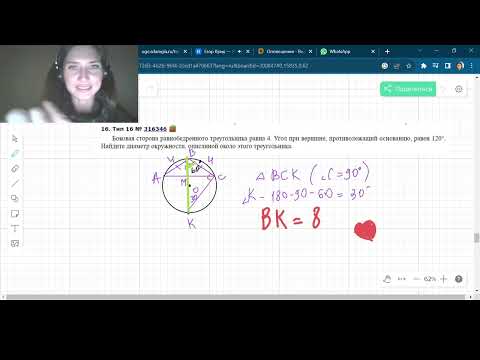
Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащей основанию, ра
Изучите примеры решения задач, чтобы лучше понять методику вычисления косинуса угла при вершине равнобедренного треугольника.
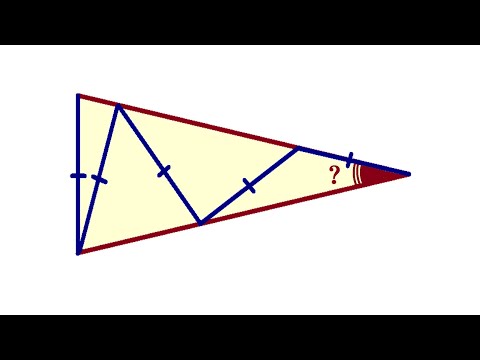
Найдите угол при вершине равнобедренного треугольника ★ Задача от Атанасяна #299

Не стесняйтесь обращаться за помощью к преподавателям или коллегам, если возникают трудности в расчетах.

Задача 6 №27620 ЕГЭ по математике. Урок 68
