Как работать с несовместными системами линейных уравнений: практические советы
Несовместная система линейных уравнений — это система, у которой нет решений. В этой статье мы рассмотрим, как определить такую систему и какие шаги предпринять для её анализа и решения.



Для определения несовместной системы проверьте ранги матрицы коэффициентов и расширенной матрицы.

Метод Гаусса. Исследование системы на совместность. Несовместная система


Используйте метод Гаусса для приведения матрицы к ступенчатому виду.

Общее, частное, базисное решение системы линейных уравнений Метод Гаусса
Если ранги матрицы коэффициентов и расширенной матрицы различны, система несовместна.

Решаем СИСТЕМЫ УРАВНЕНИЙ с двумя неизвестными С НУЛЯ - Саша Тёплая - 100балльный


Проверяйте наличие противоречий в системе уравнений.
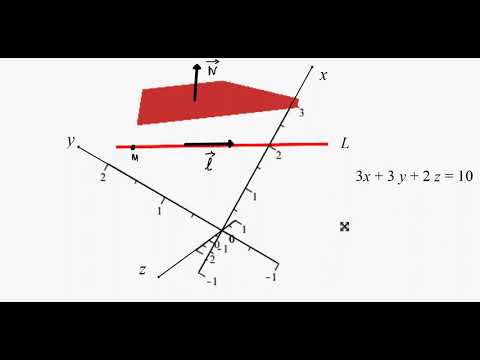
622. Несовместная система линейных алгебраических уравнений

Используйте графическое представление для визуализации системы уравнений.

Решение систем линейных уравнений методом Гаусса. Несовместные системы.

При решении обратите внимание на числовые коэффициенты, чтобы избежать ошибок.

Математика без Ху%!ни. Метод Гаусса. Совместность системы. Ранг матрицы.


Изучите теорию линейной алгебры для глубокого понимания методов решения.
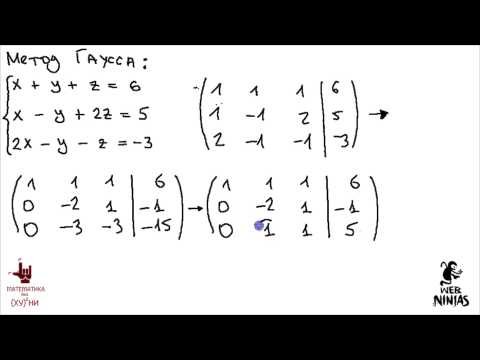
Математика без Ху%!ни. Метод Гаусса.


Практикуйтесь на примерах различных систем уравнений для лучшего усвоения материала.
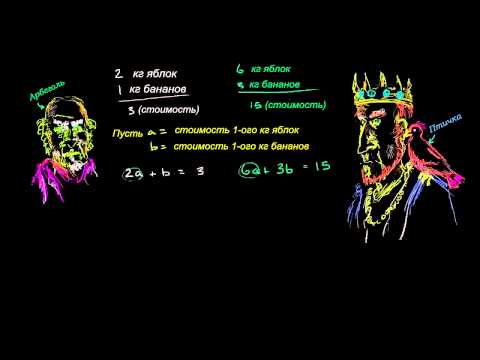
Несовместные системы уравнений

Решение систем линейных уравнений Несовместные системы

Обращайтесь к специализированной литературе для получения дополнительной информации.

Совместные и несовместные, определенные и неопределенные системы линейных уравнений


Используйте программное обеспечение для решения сложных систем уравнений.