Формула расчета скорости на наклонной плоскости: понятное руководство
В этой статье вы узнаете, как правильно рассчитать скорость объекта, скользящего по наклонной плоскости. Мы объясним основные принципы, формулы и предоставим примеры для лучшего понимания.


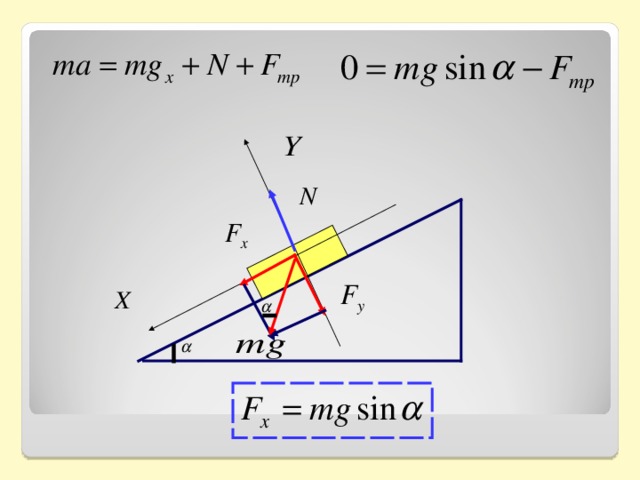
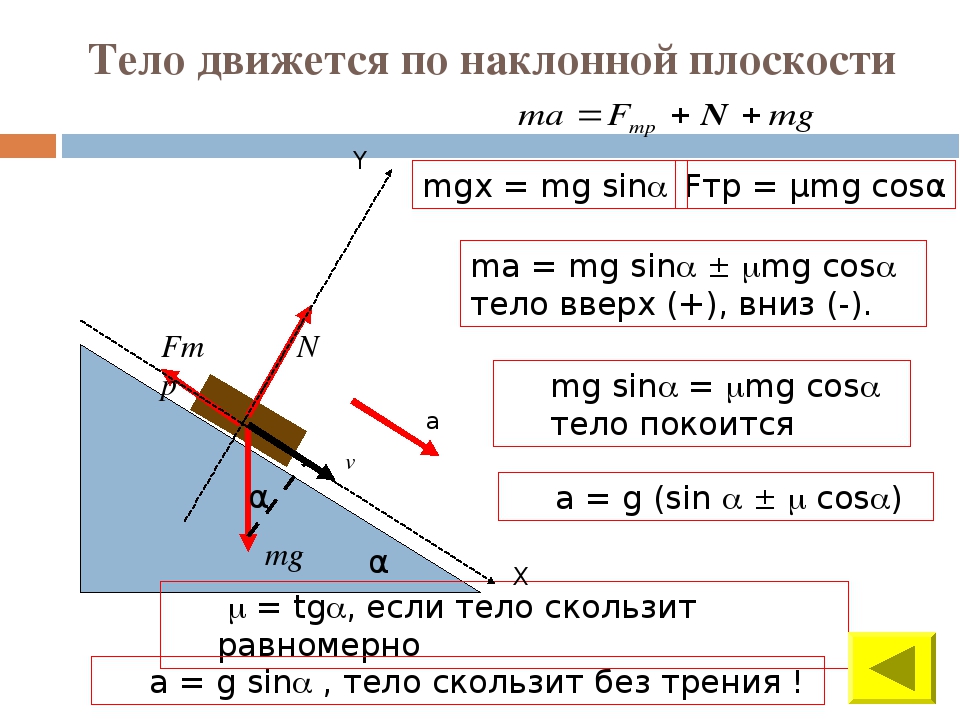
Для вычисления скорости объекта, скользящего по наклонной плоскости, используйте формулу v = sqrt(2 * g * h / sin^2(θ)), где g — ускорение свободного падения, h — высота, θ — угол наклона плоскости.

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 класс

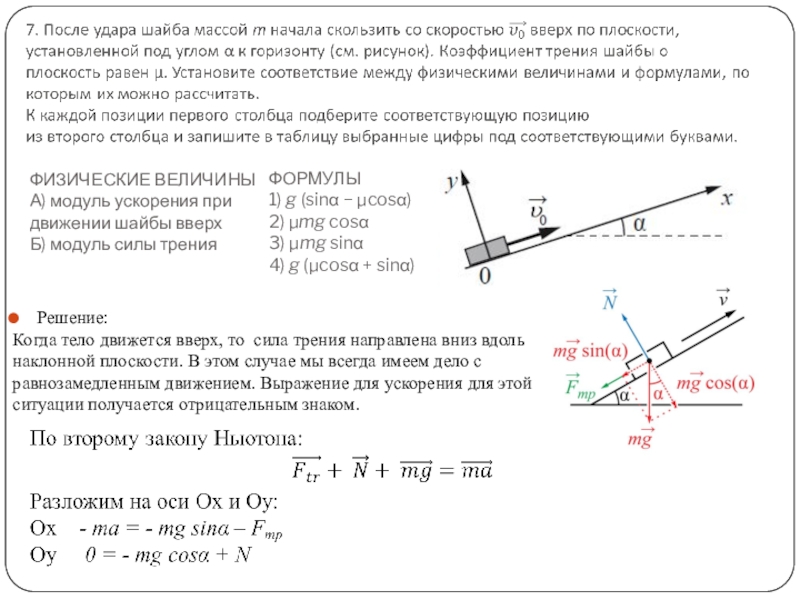
Убедитесь, что правильно измеряете угол наклона и высоту, так как погрешности в этих данных могут значительно повлиять на результат расчета скорости.

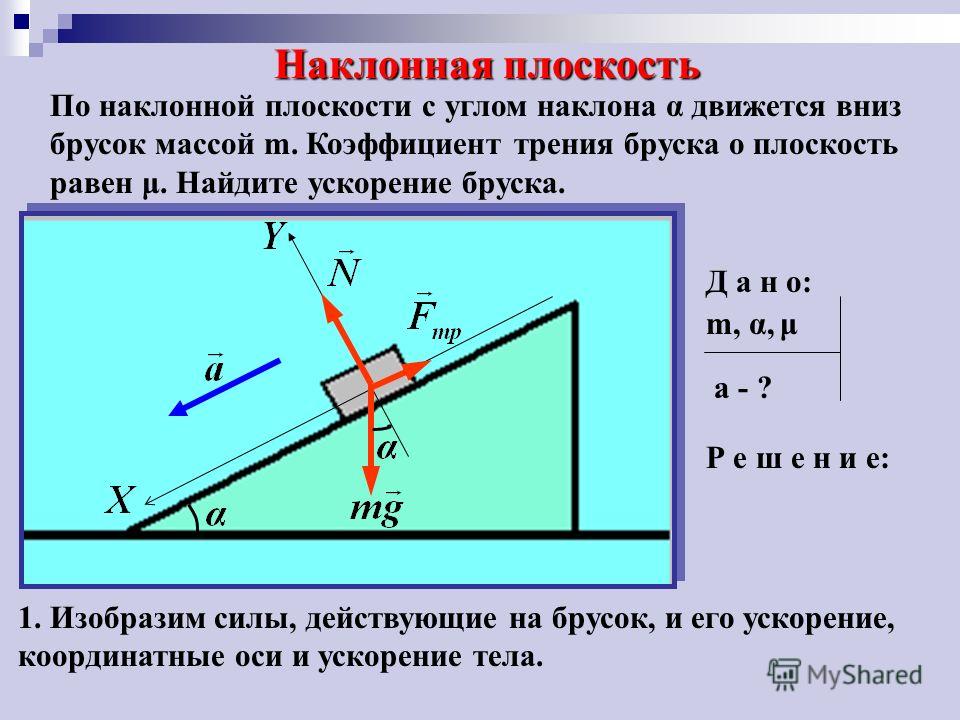
Соскальзывание бруска с наклонной плоскости.
При решении задач с наклонной плоскостью учитывайте силу трения, если это важно для вашей задачи, так как она может замедлить скорость объекта.

Урок 87. Движение по наклонной плоскости (ч.1)
Если необходимо провести точные расчеты, используйте калькуляторы или специальные программы для физики, которые помогут вам избежать ошибок в вычислениях.

Урок 101. Скатывание тела с наклонной плоскости

Перед началом расчетов проверьте, что ваши измерения единиц соответствуют системе, используемой в формуле (например, метры и секунды).

Скатывание цилиндров с наклонной плоскости

При выполнении практических экспериментов убедитесь, что поверхность наклонной плоскости гладкая и не содержит неровностей, чтобы минимизировать влияние трения.

Лабораторная работа 1. Определение ускорения тела, движущегося по наклонной плоскости
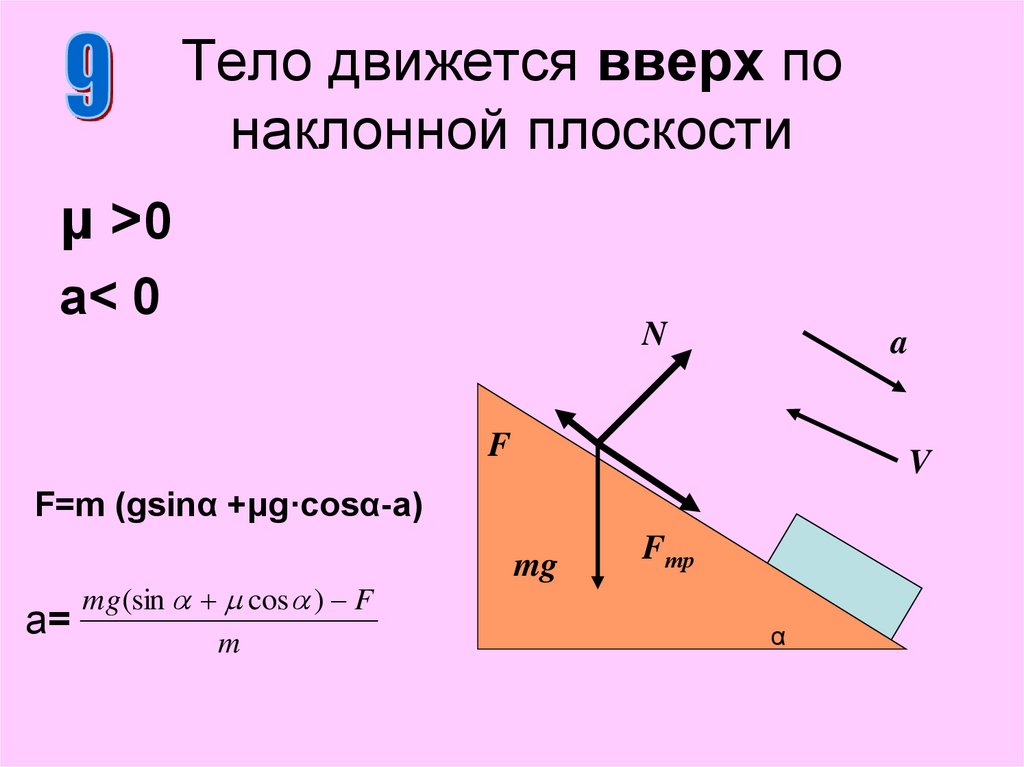
Используйте графики и диаграммы для визуализации зависимостей между переменными, такими как угол наклона и скорость, чтобы лучше понять физические процессы.
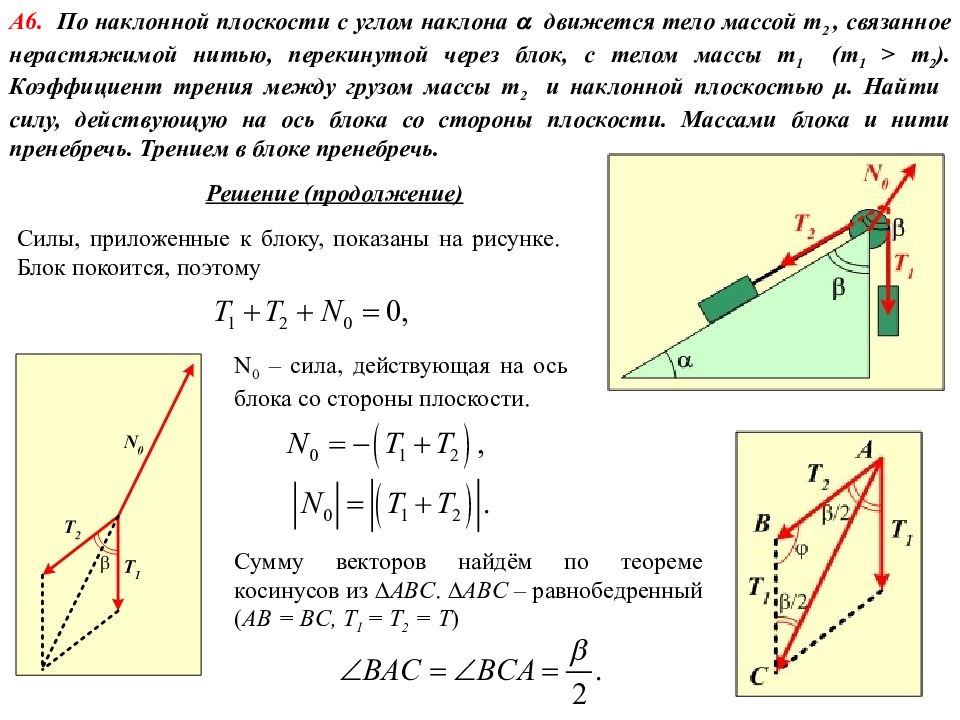
Решайте практические задачи и примеры, чтобы закрепить понимание формулы и принципов расчета скорости на наклонной плоскости.
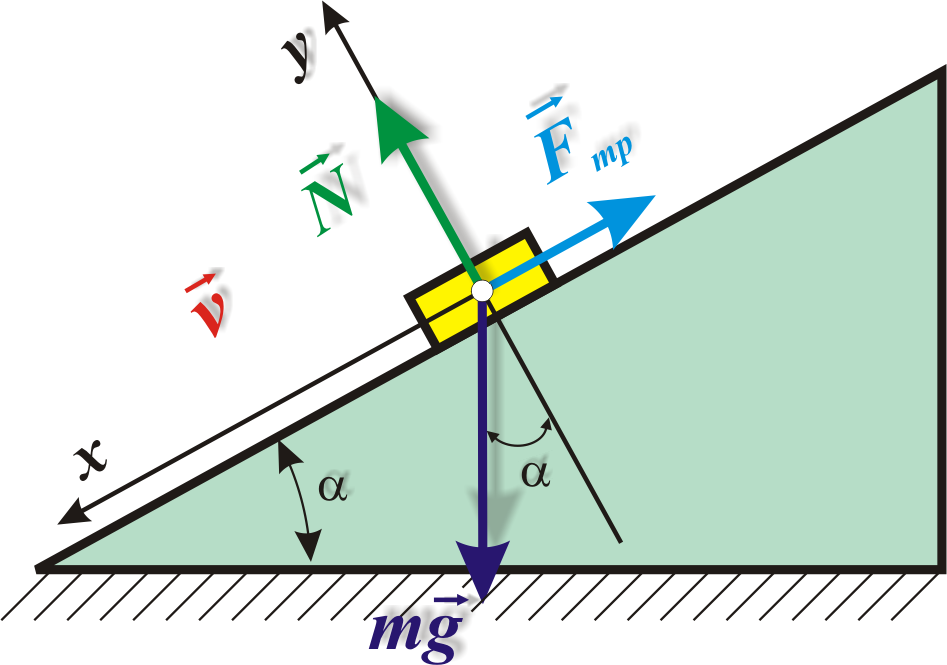
Обратите внимание на единицы измерения, чтобы избежать ошибок в расчетах. Например, если высота дана в сантиметрах, преобразуйте ее в метры.

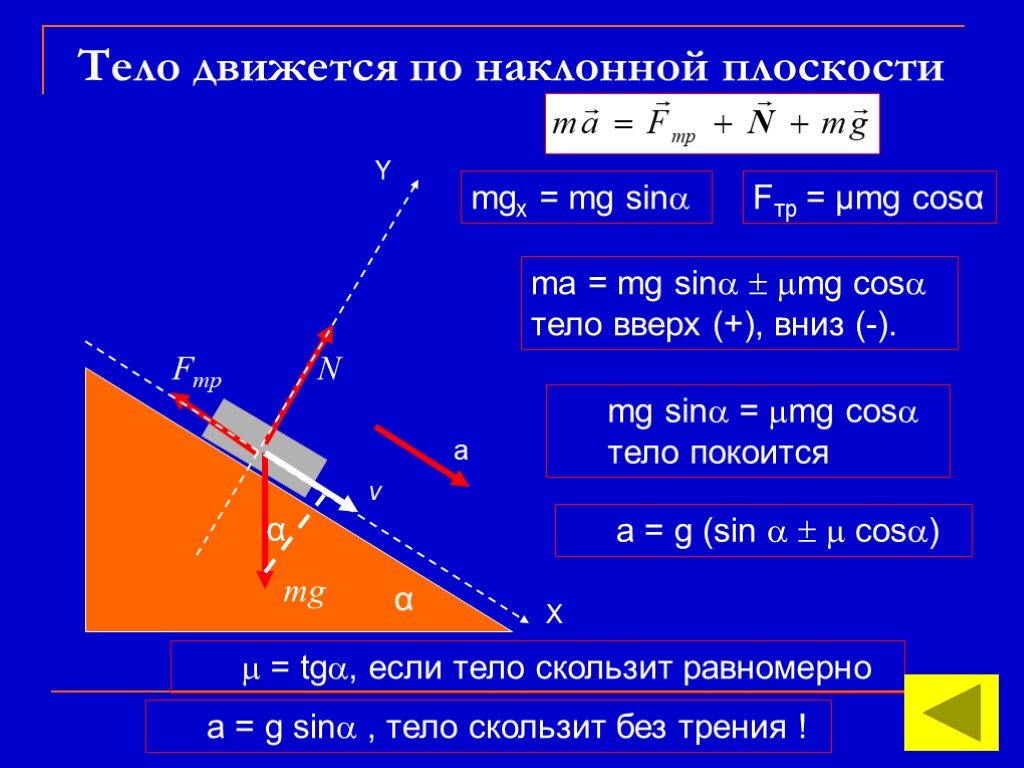
Включайте в свои расчеты погрешности измерений, чтобы получить более точные результаты и учитывать возможные отклонения.