Ключевые свойства центрального угла и их применение
Центральный угол - это угол, вершина которого находится в центре окружности, а стороны проходят через две точки на окружности. Он имеет важные свойства, которые находят применение в различных задачах геометрии.
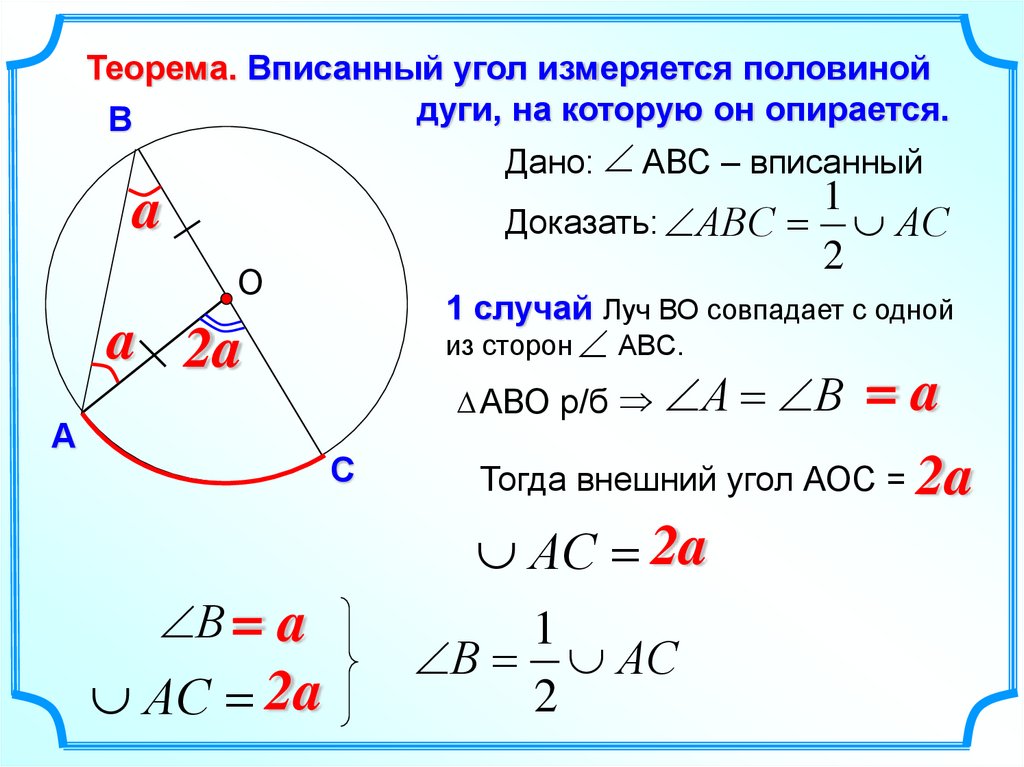

Всё про вписанные и центральные углы за 4 минуты - Борис Трушин -
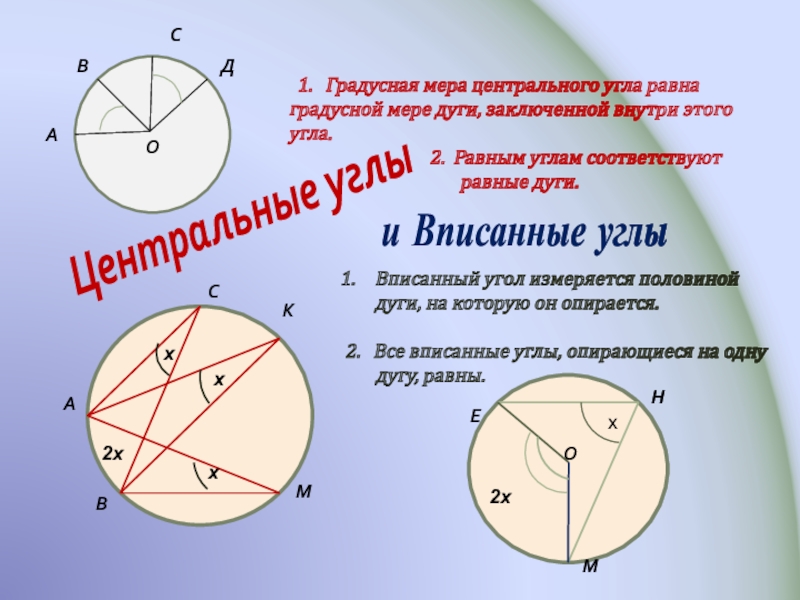
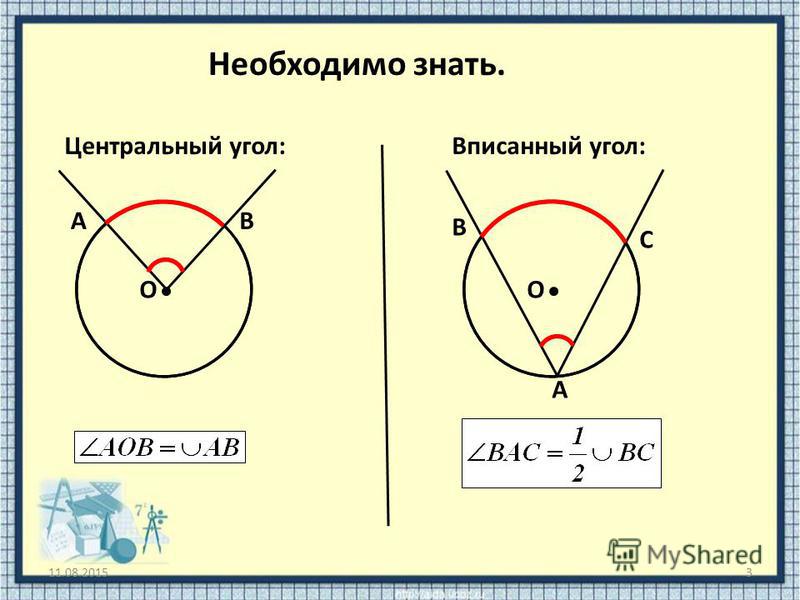
Сумма всех центральных углов, исходящих из одного центра, равна 360 градусам.

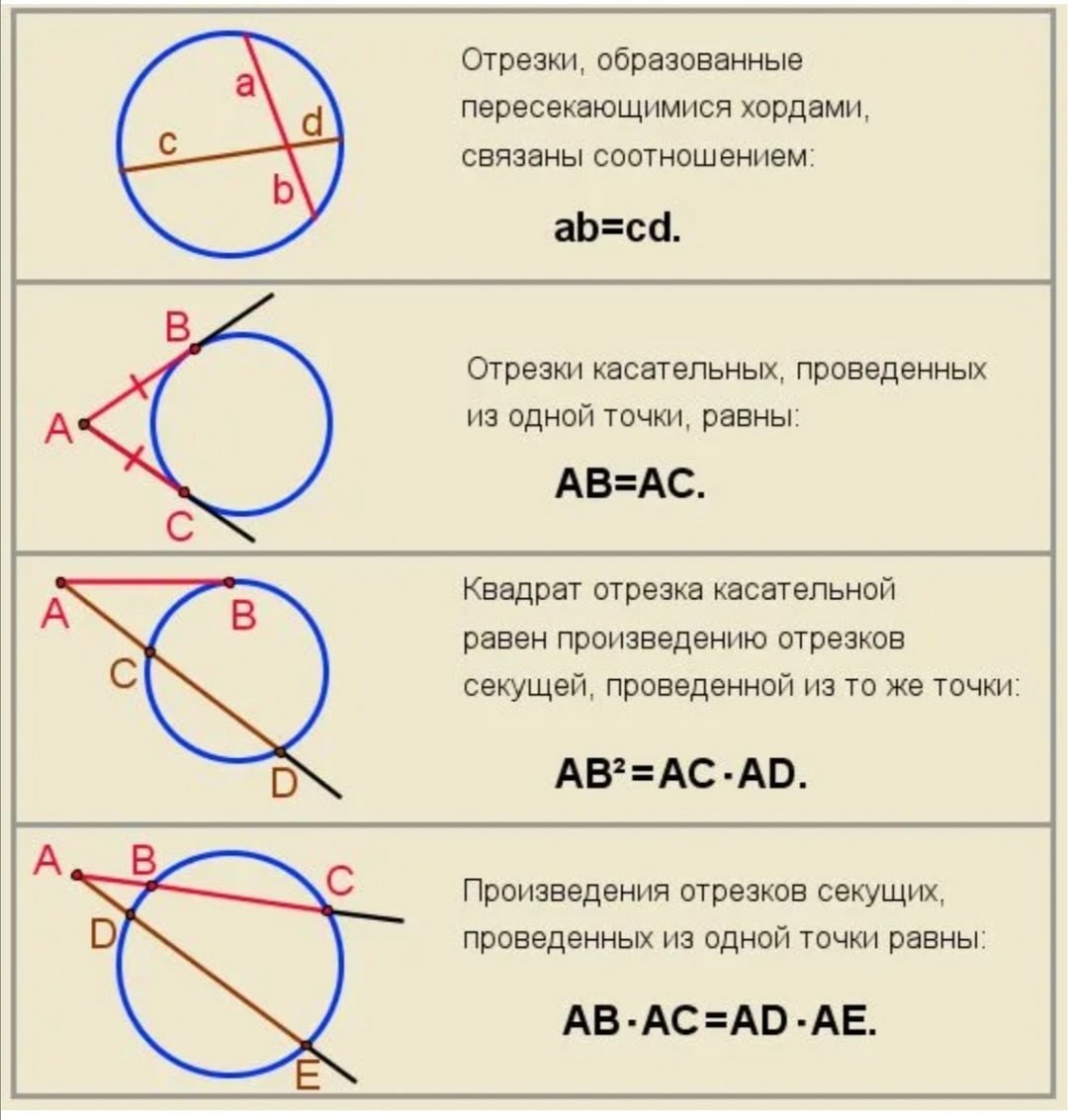
Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.
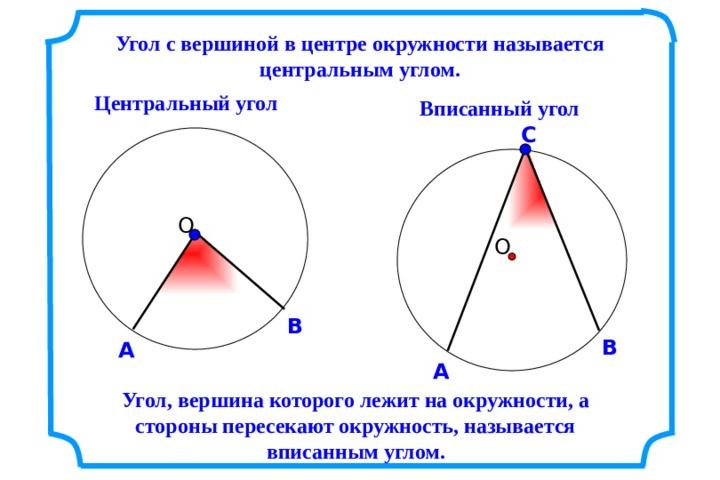
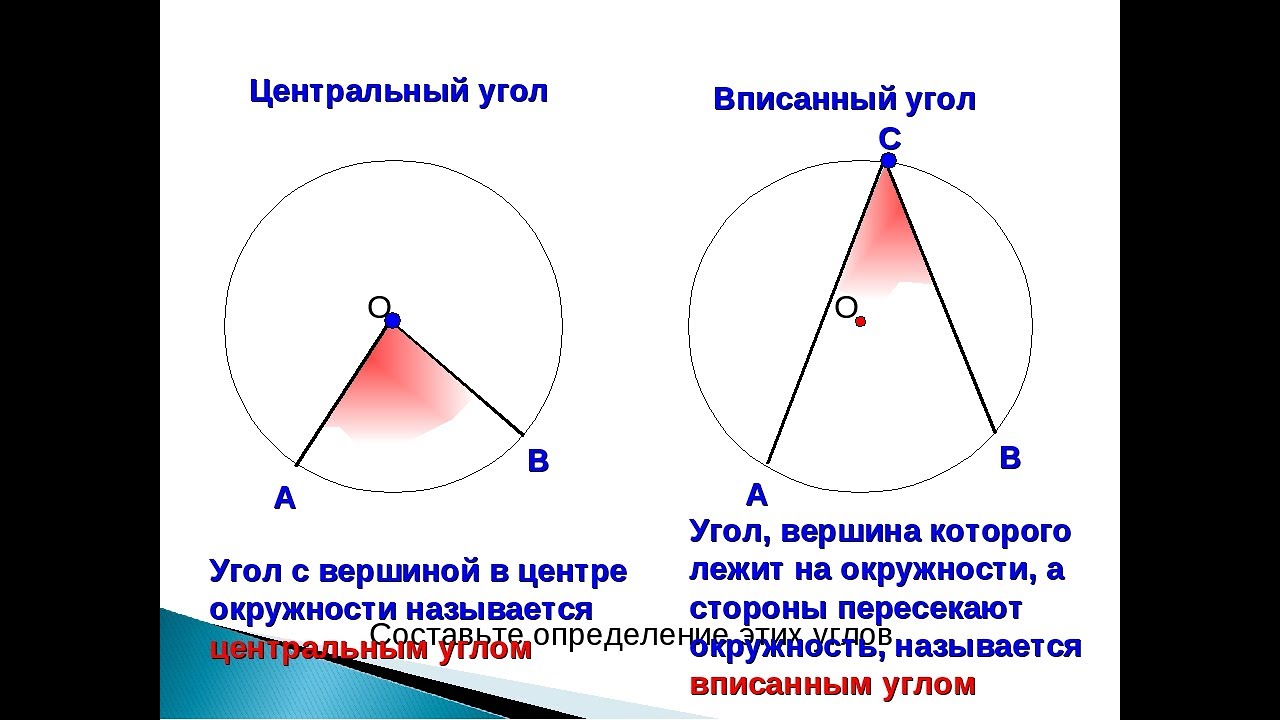
Если два центральных угла опираются на одинаковые дуги, то они равны.

Углы, вписанные в окружность. 9 класс.

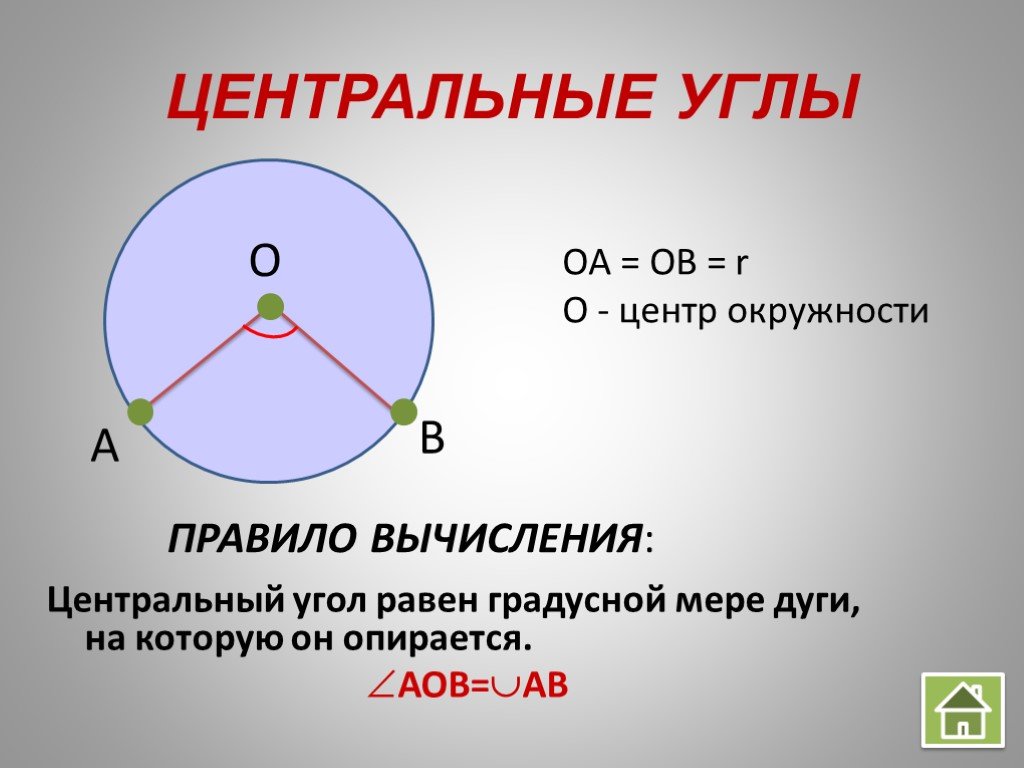
Центральный угол в полукруге всегда равен 180 градусам.

Центральные и вписанные углы - геометрия 8 класс

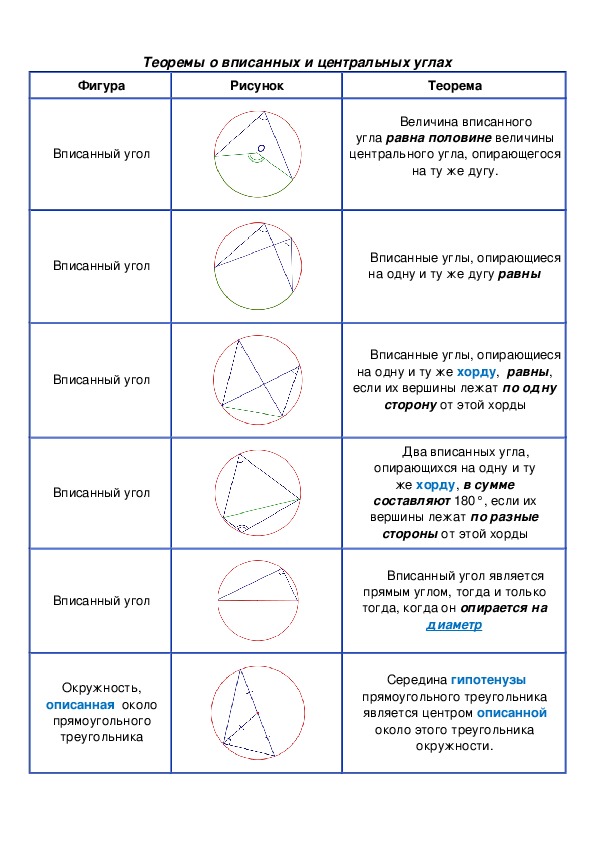
Центральный угол, опирающийся на меньшую дугу, всегда меньше угла, опирающегося на большую дугу.

Всё про углы в окружности. Геометрия - Математика
Для вычисления центрального угла используйте формулу: угол = дуга / радиус.
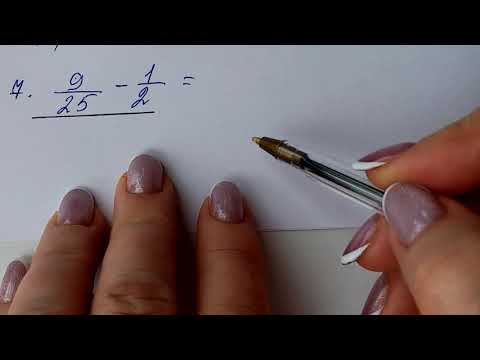
ОГЭ для НОЛИКОВ. Задание-6
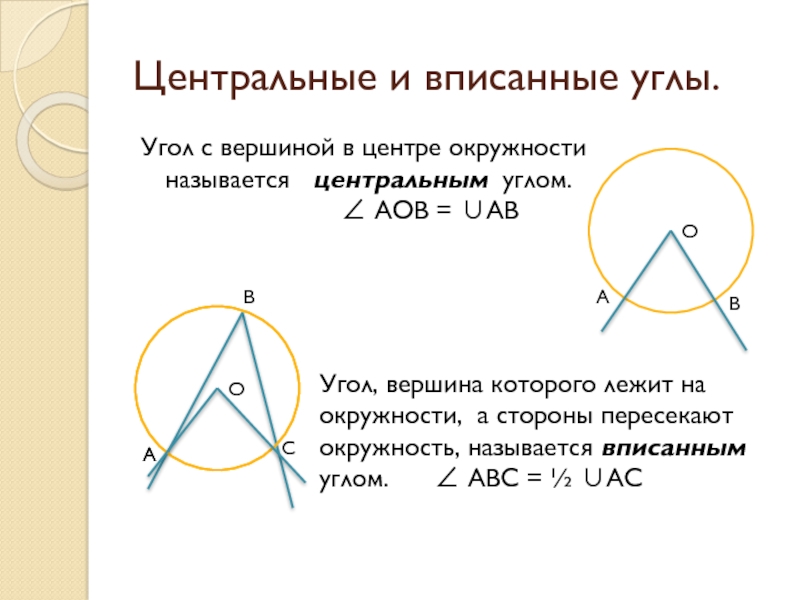
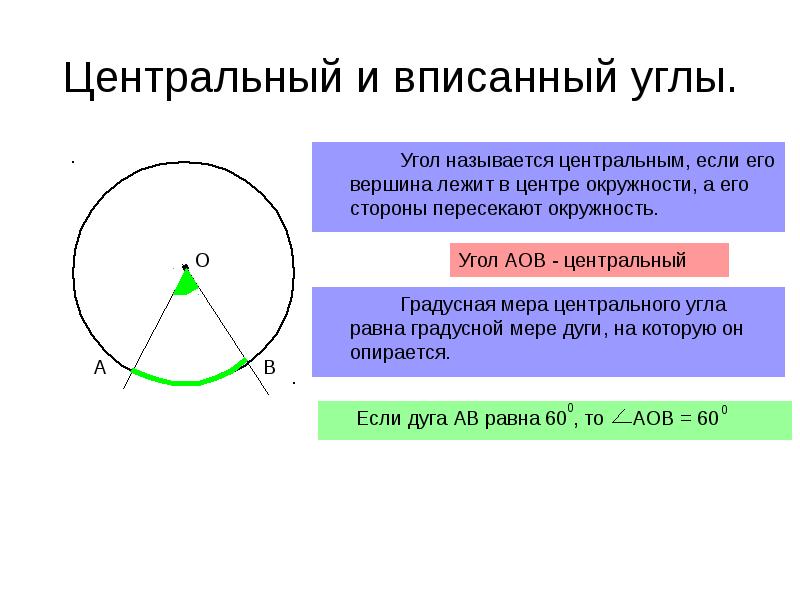
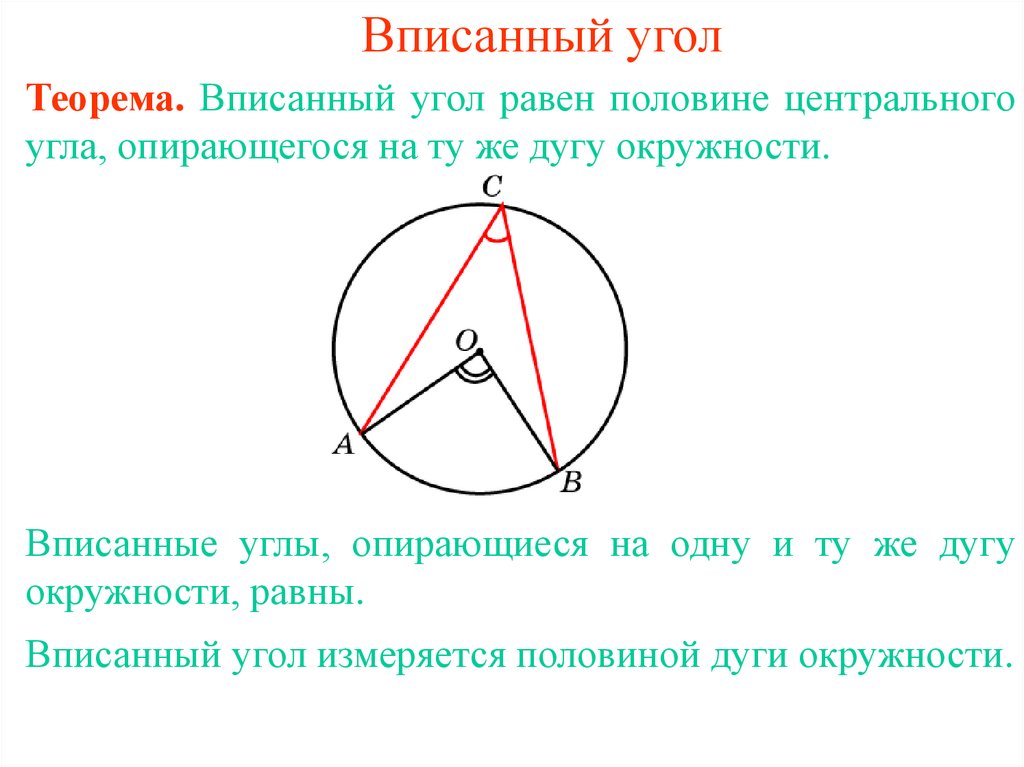
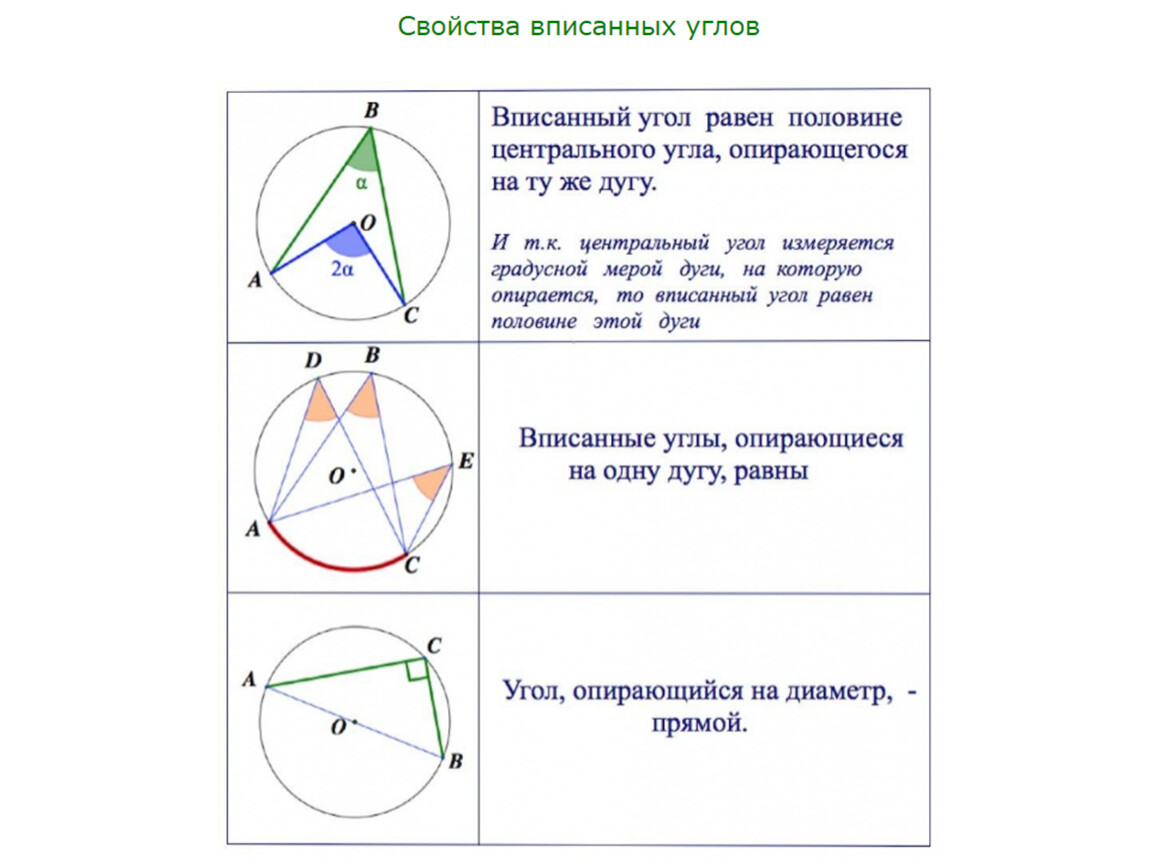
Центральный угол и соответствующий ему вписанный угол всегда соотносятся как 2:1.

В задачах на нахождение длины дуги, зная центральный угол, можно использовать формулу: длина дуги = радиус * угол (в радианах).
Центральный угол помогает в построении правильных многоугольников, так как центральный угол каждого сектора равен 360 градусам, деленным на число сторон многоугольника.

Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСС
Использование свойств центрального угла упрощает решение многих задач по геометрии, связанных с окружностями и дугами.

ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный Угол