Понимание свойств биссектрисы треугольника и их роль в подобии
В данном разделе представлены основные свойства биссектрисы треугольника и их связь с подобием треугольников. Эти свойства играют ключевую роль в различных геометрических задачах и доказательствах.
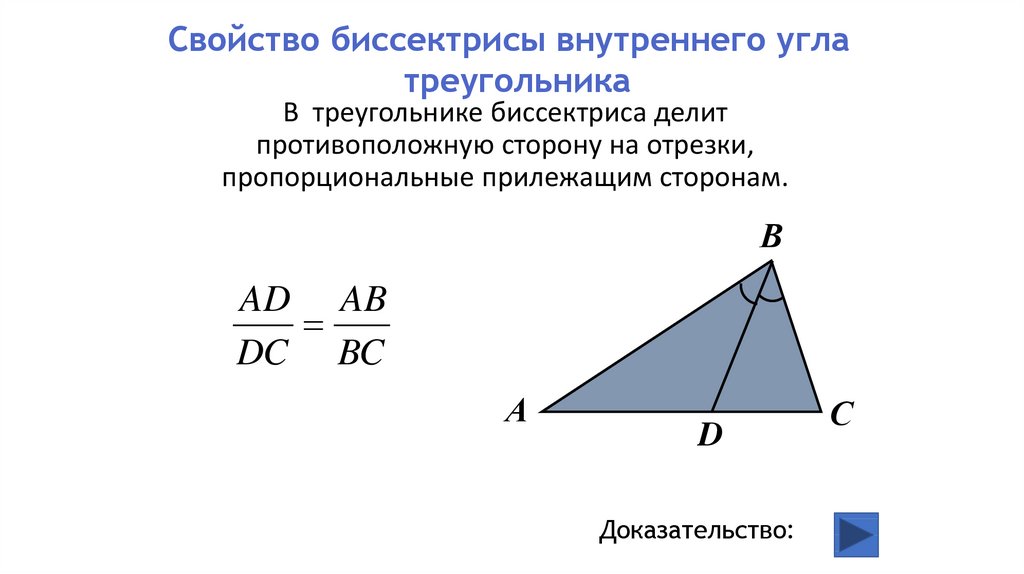
Проверьте, что биссектрисы треугольника пересекаются в одной точке, называемой инцентром, и эта точка равноудалена от всех сторон треугольника.
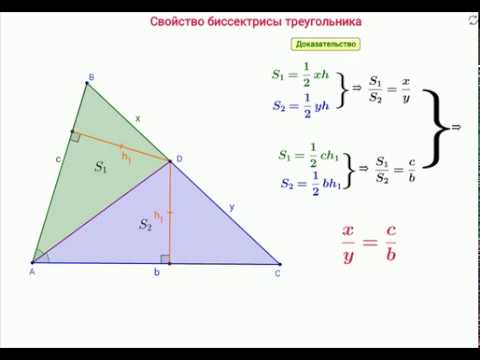
Свойство биссектрисы треугольника

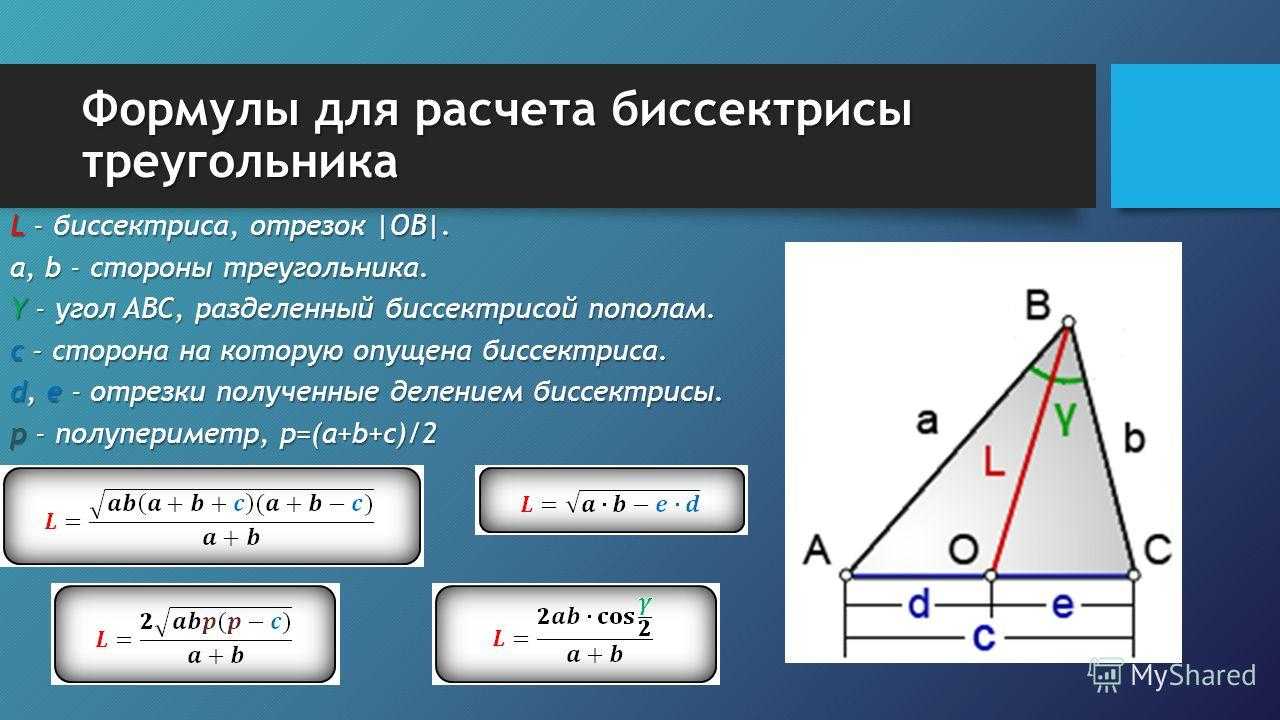
Используйте свойства биссектрисы для доказательства подобия треугольников, так как угол между биссектрисами может дать подсказки о соотношении сторон.

Задание 26 Свойство биссектрисы треугольника Подобные треугольники
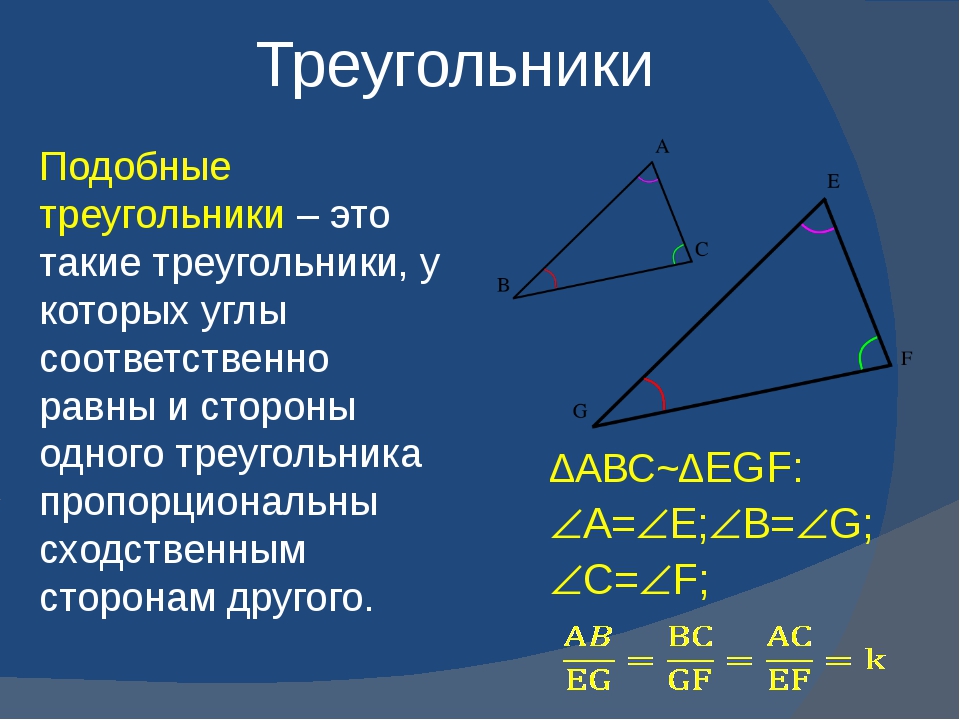
Не забывайте, что биссектрисы треугольника делят углы на два равных угла, что может быть полезно для вычисления углов в сложных задачах.
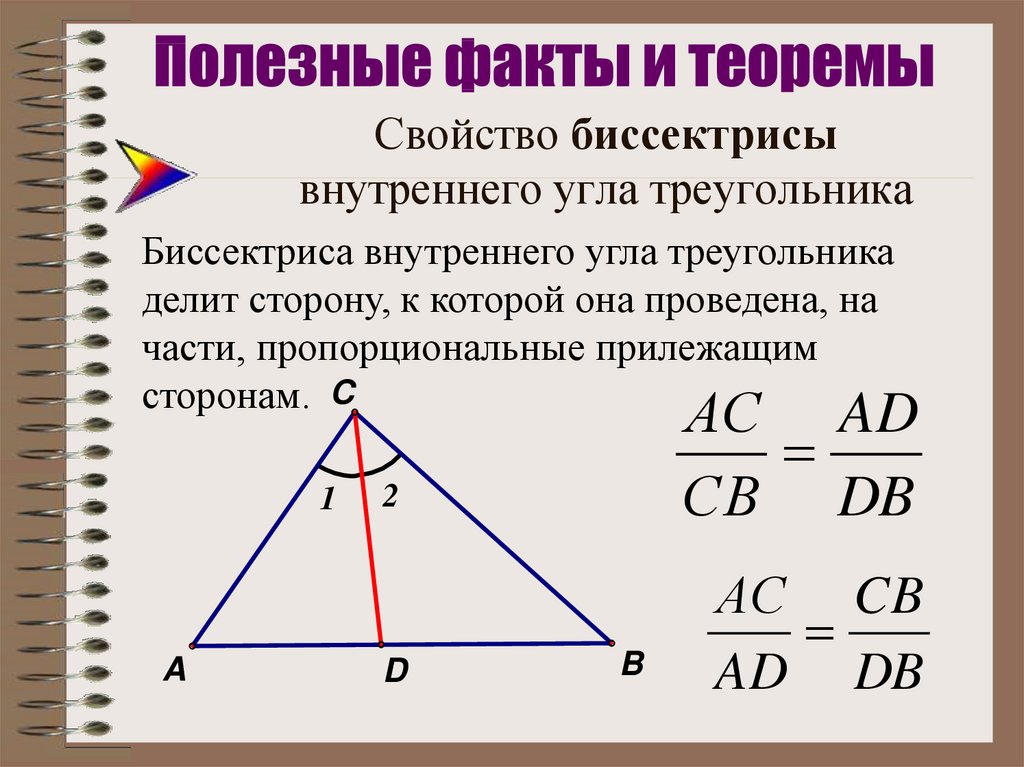
Найдите биссектрису треугольника
Если вам нужно найти длину отрезка, соединяющего точку на биссектрисе с противоположной стороной треугольника, используйте теорему о биссектрисе.

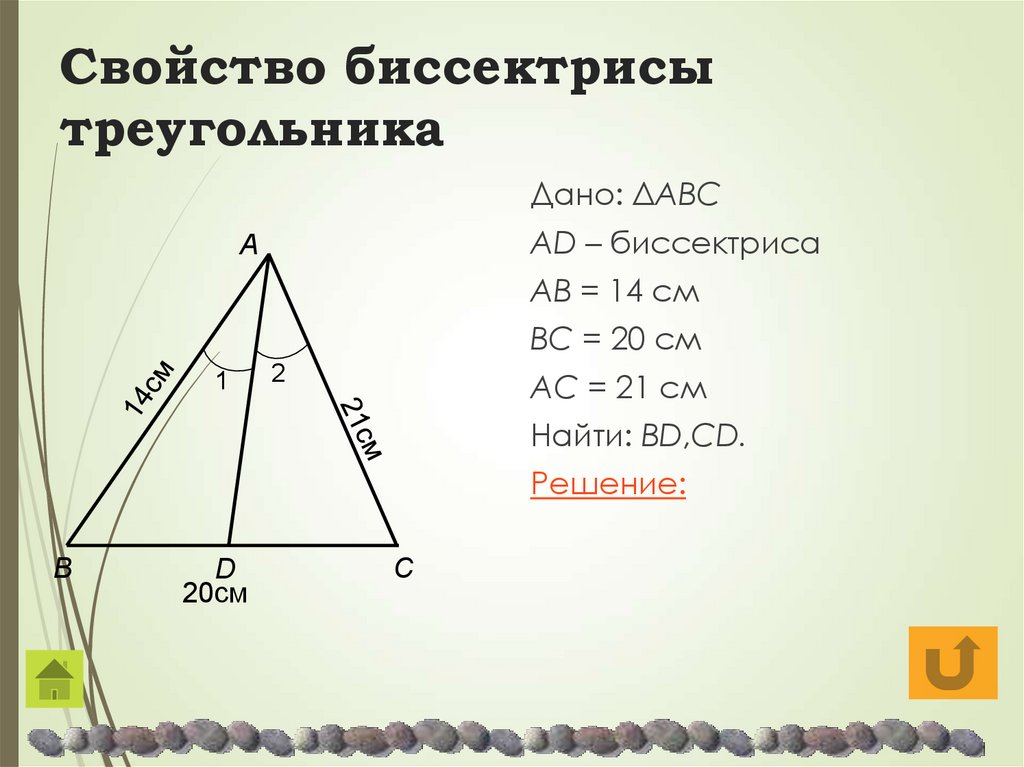
Свойство биссектрисы треугольника
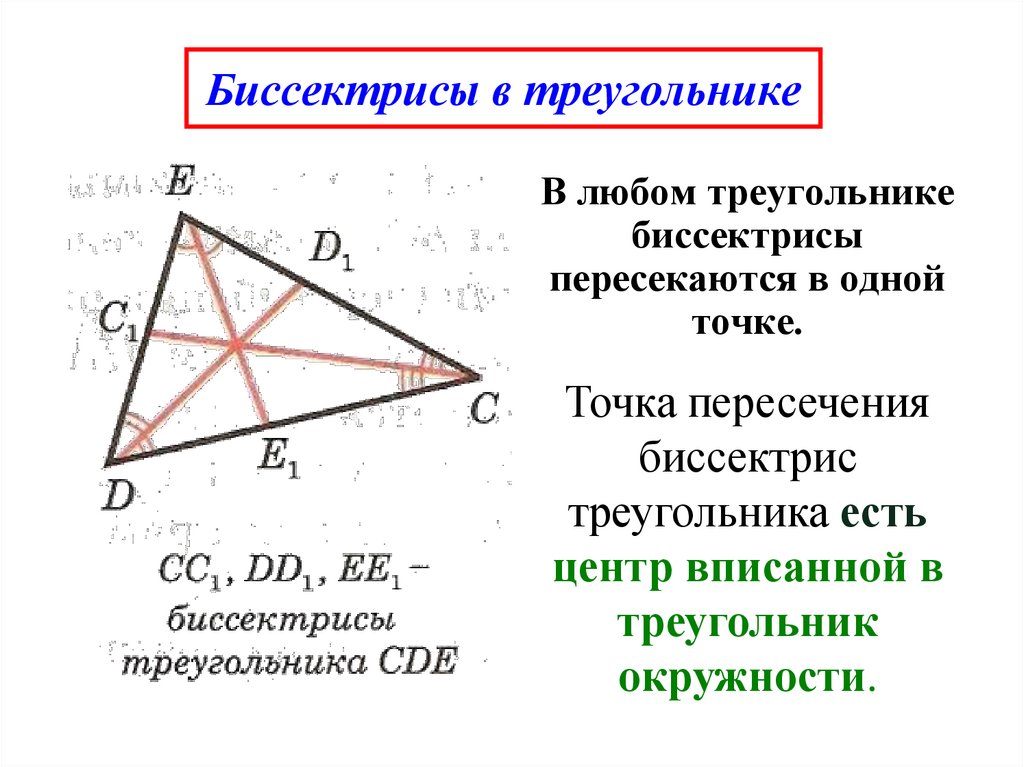
В задачах на подобие треугольников, применение свойств биссектрисы может упростить вычисления и доказательства.

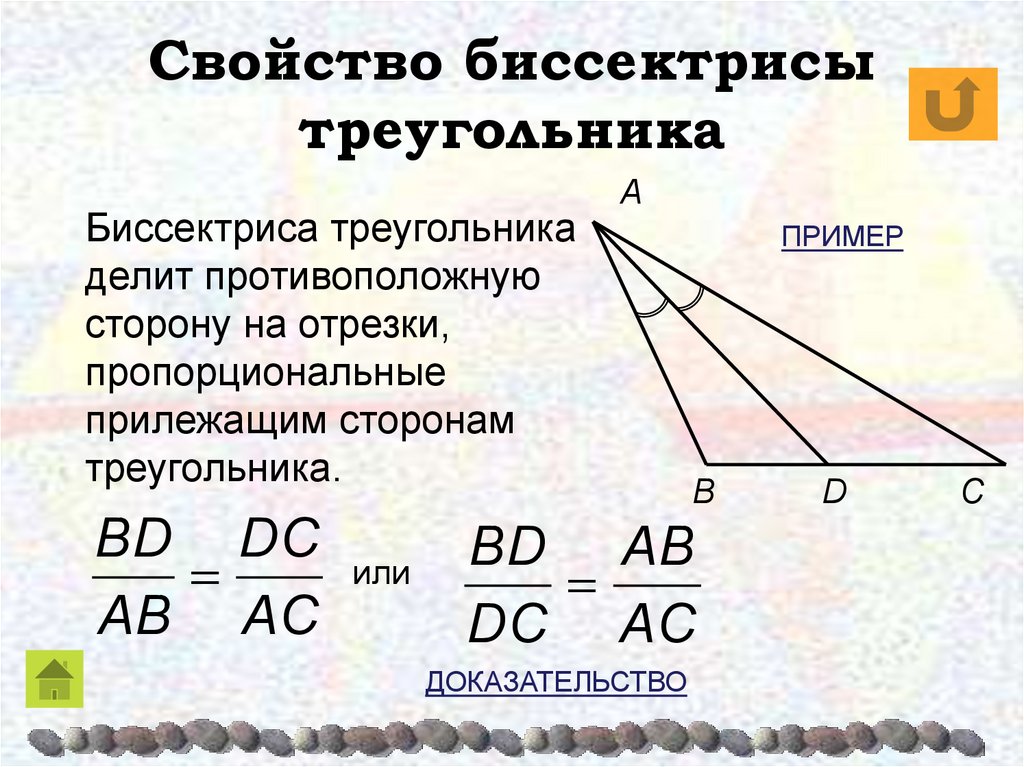
Свойство биссектрисы треугольника с доказательством
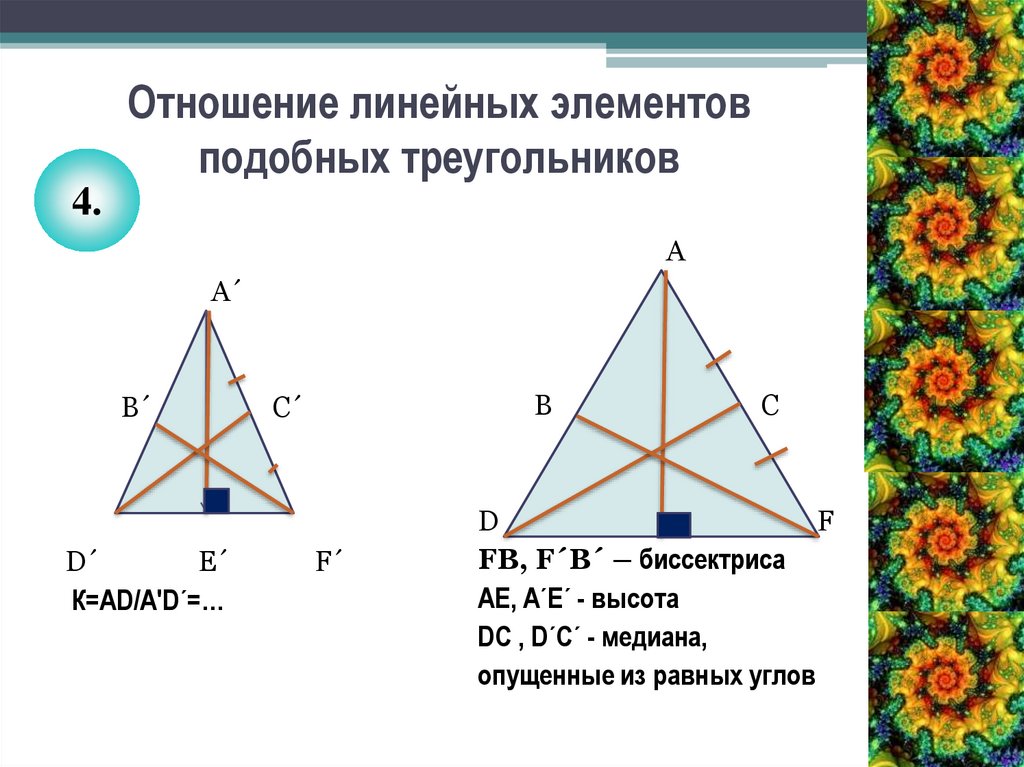
Помните, что в треугольниках, где биссектрисы делят углы, отношения между сторонами могут помочь в решении геометрических задач.
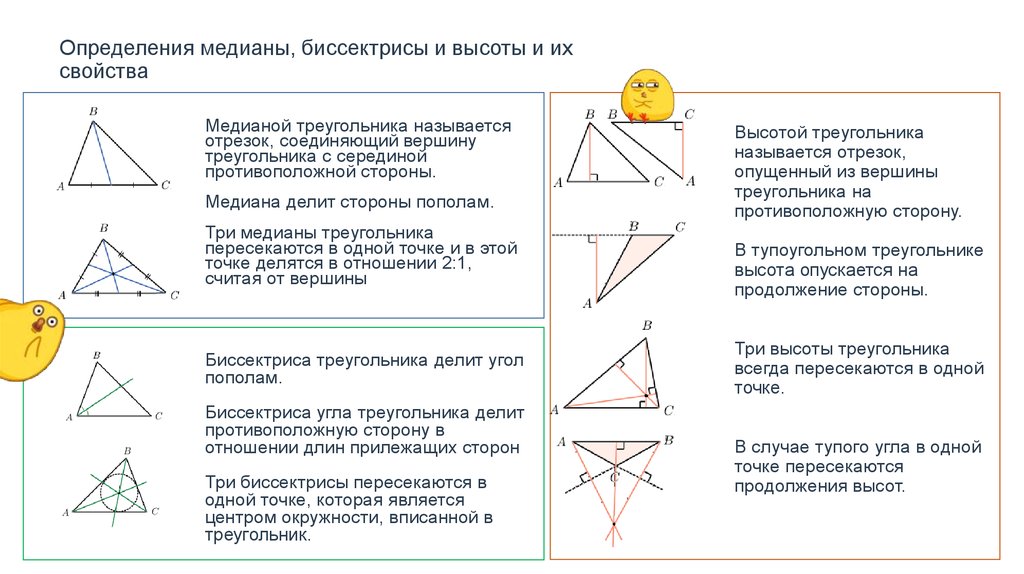
Для лучшего понимания свойств биссектрисы, рассмотрите различные примеры и задачи, в которых они применяются.

Парабола. Что это такое? - Открытый онлайн-урок
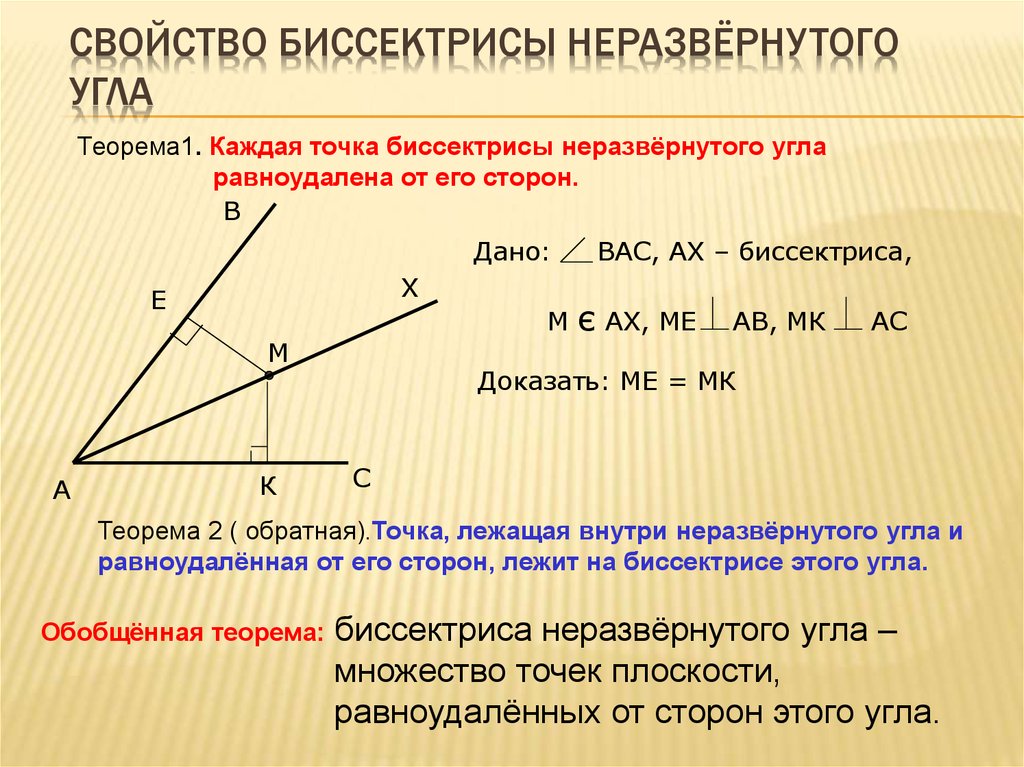
Исследуйте, как изменения в длине биссектрисы влияют на размер треугольника и его стороны.
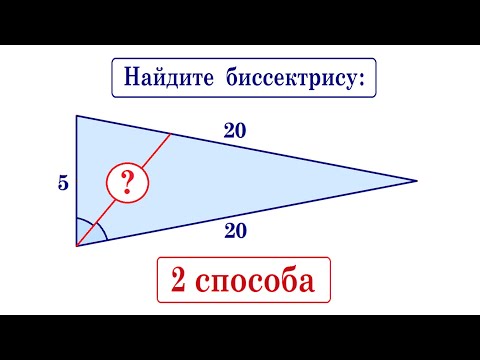
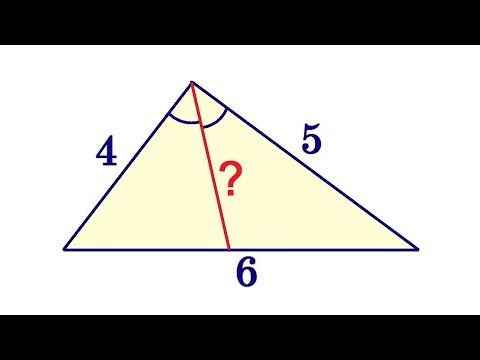
Найдите биссектрису угла треугольника на рисунке ★ Два способа

Свойство биссектрисы треугольника.
Рассмотрите использование биссектрисы в доказательствах теорем о подобии и равенстве треугольников.
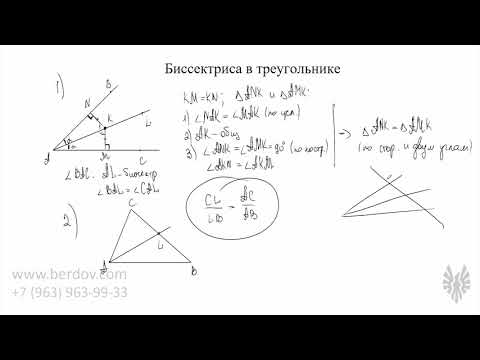
Биссектриса в треугольнике

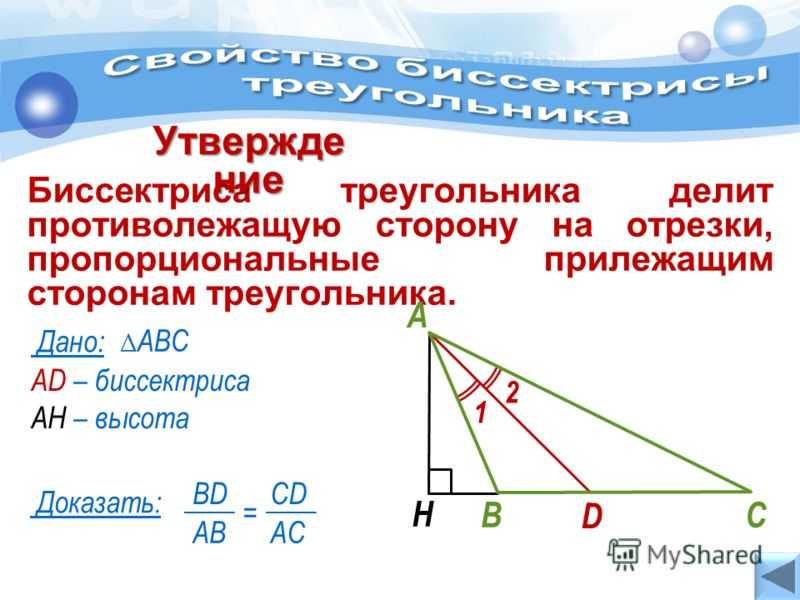
Изучите различные способы построения биссектрис в треугольнике для более глубокого понимания их свойств.
