Три высоты треугольника и их пересечение в одной точке
Три высоты любого треугольника пересекаются в одной точке, называемой ортоцентром. Это важное свойство треугольников используется в геометрии и имеет множество практических применений.

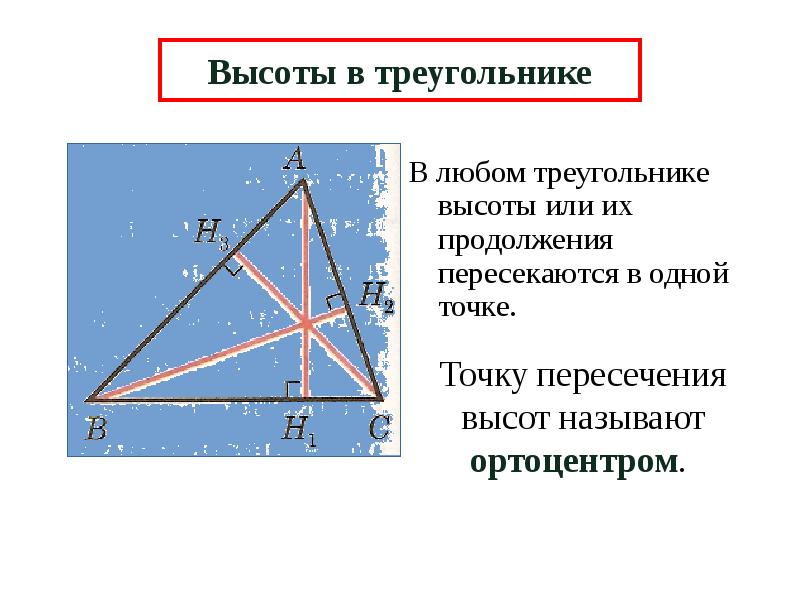
Для построения высоты треугольника проведите перпендикуляр из вершины на противоположную сторону.
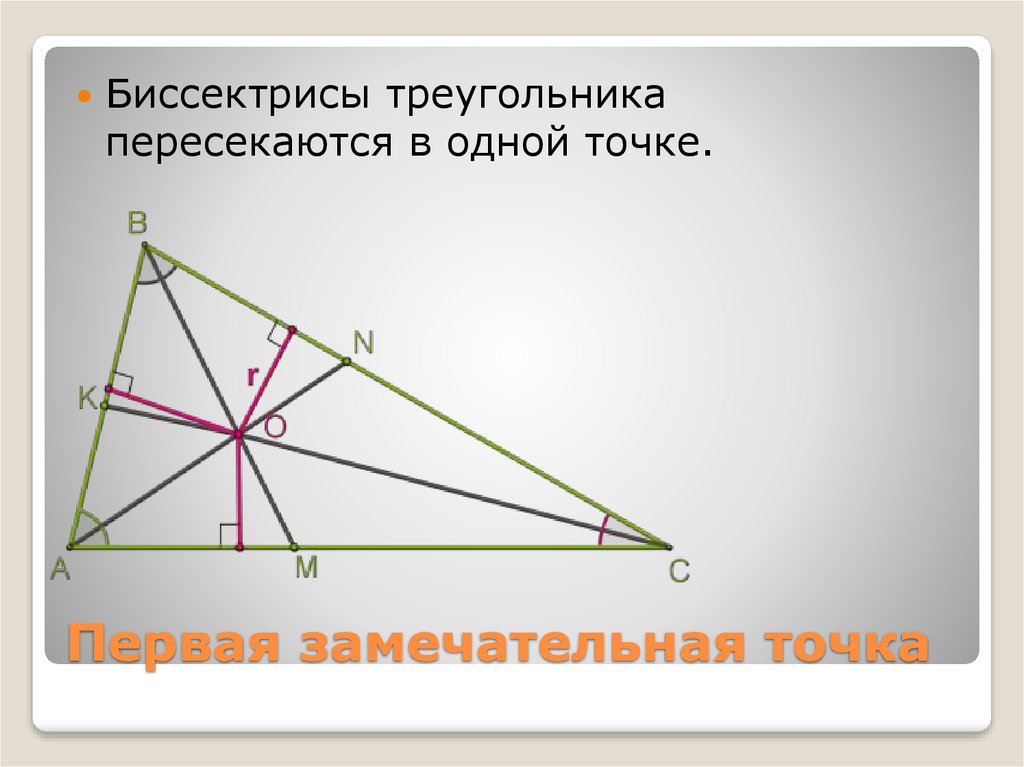
Как доказать, что биссектрисы треугольника пересекаются в одной точке?
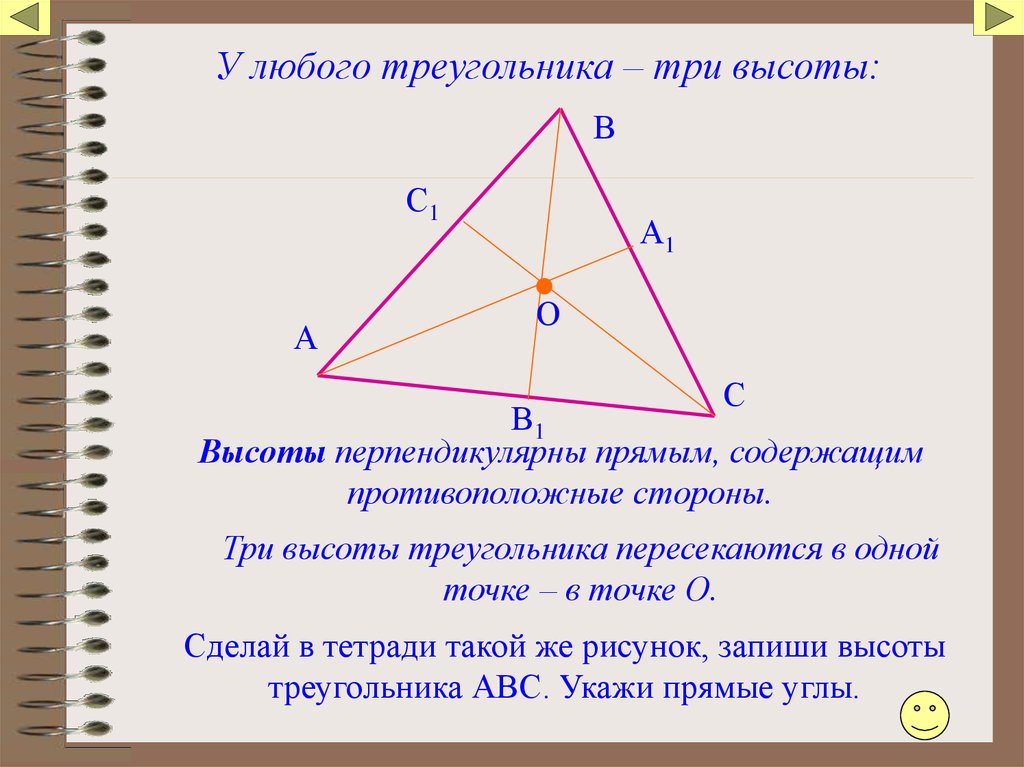

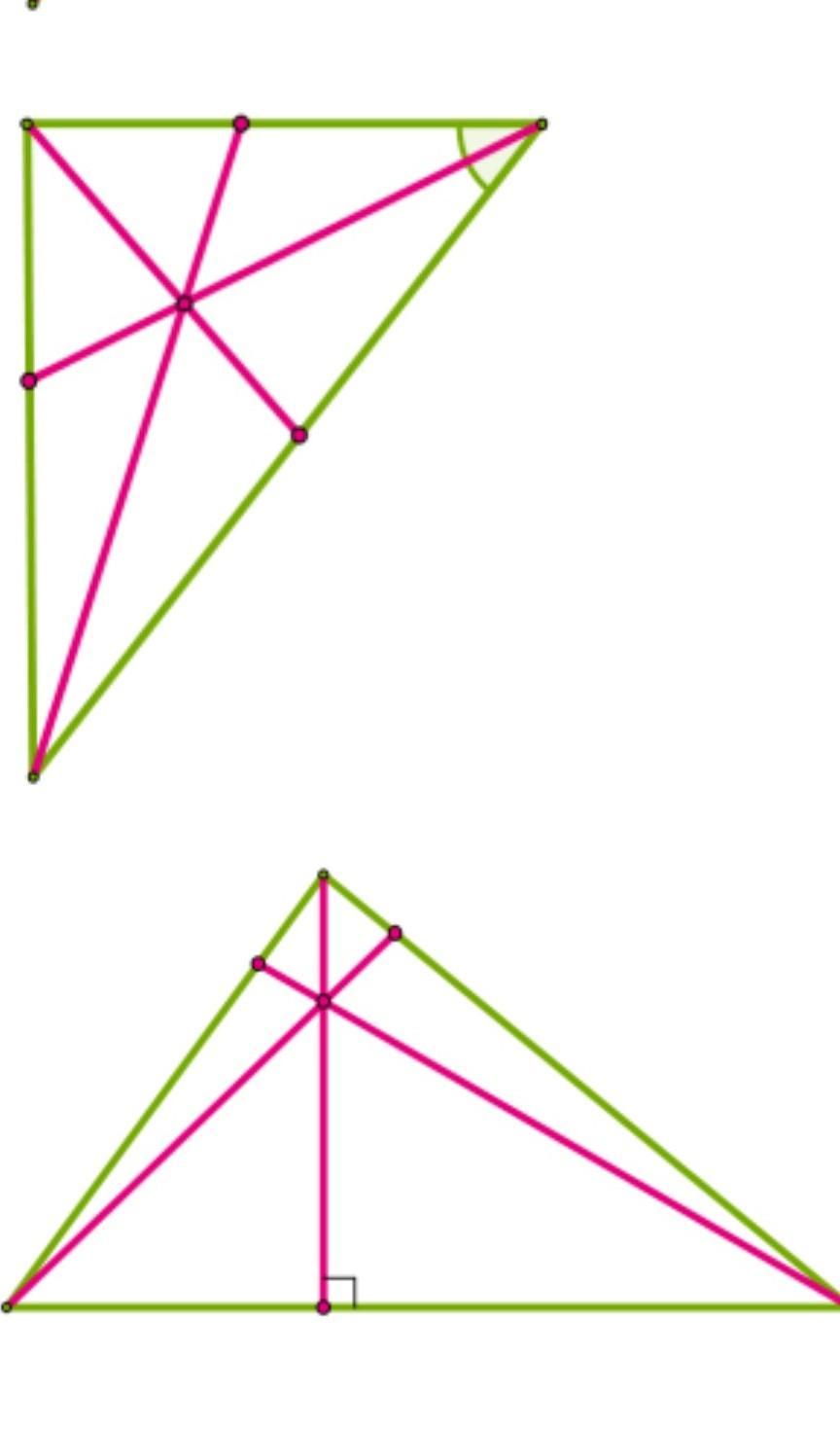
Высоты треугольника могут выходить за его пределы, если треугольник тупоугольный.
Высоты треугольника пересекаются в одной точке
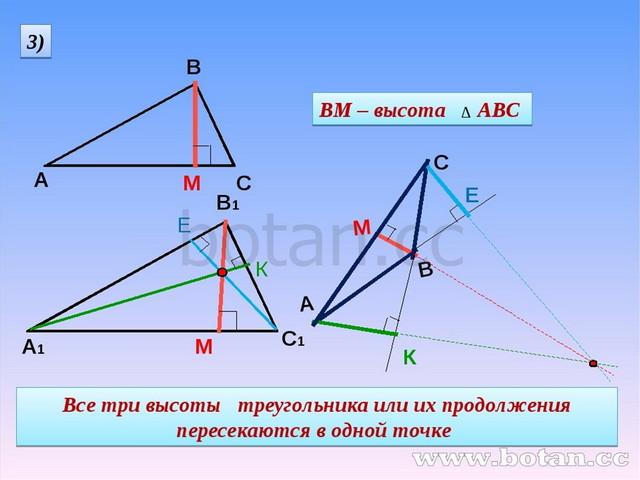
Пересечение высот треугольника называется ортоцентром.
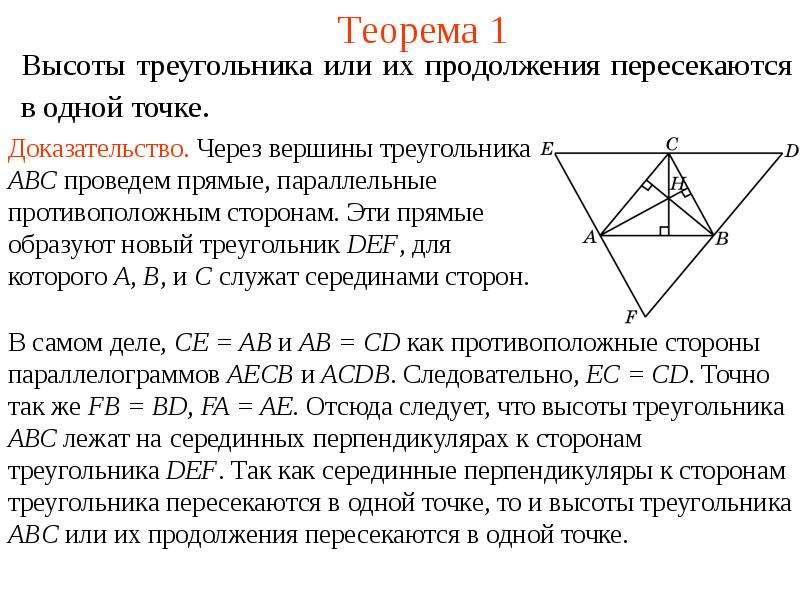
Как доказать, что высоты треугольника пересекаются в одной точке?
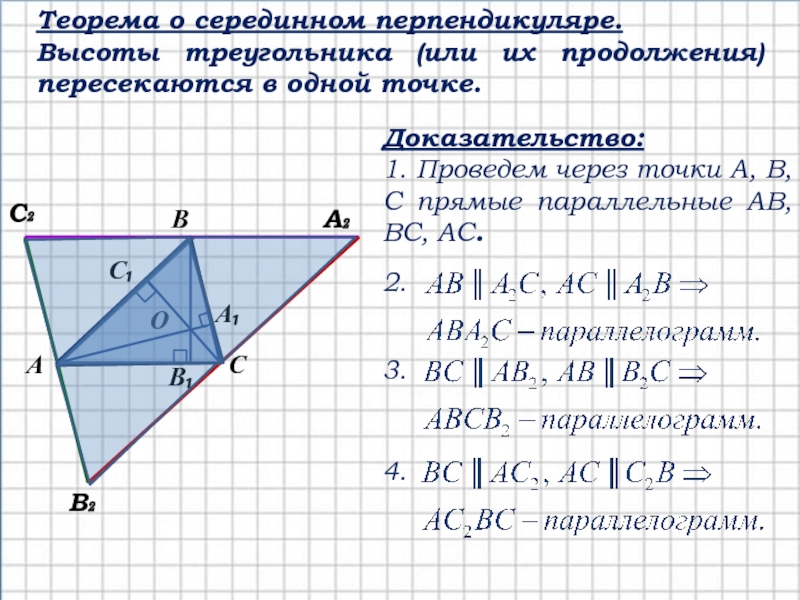
Высоты в равностороннем треугольнике также являются медианами и биссектрисами.

8 класс, 37 урок, Теорема о пересечении высот треугольника
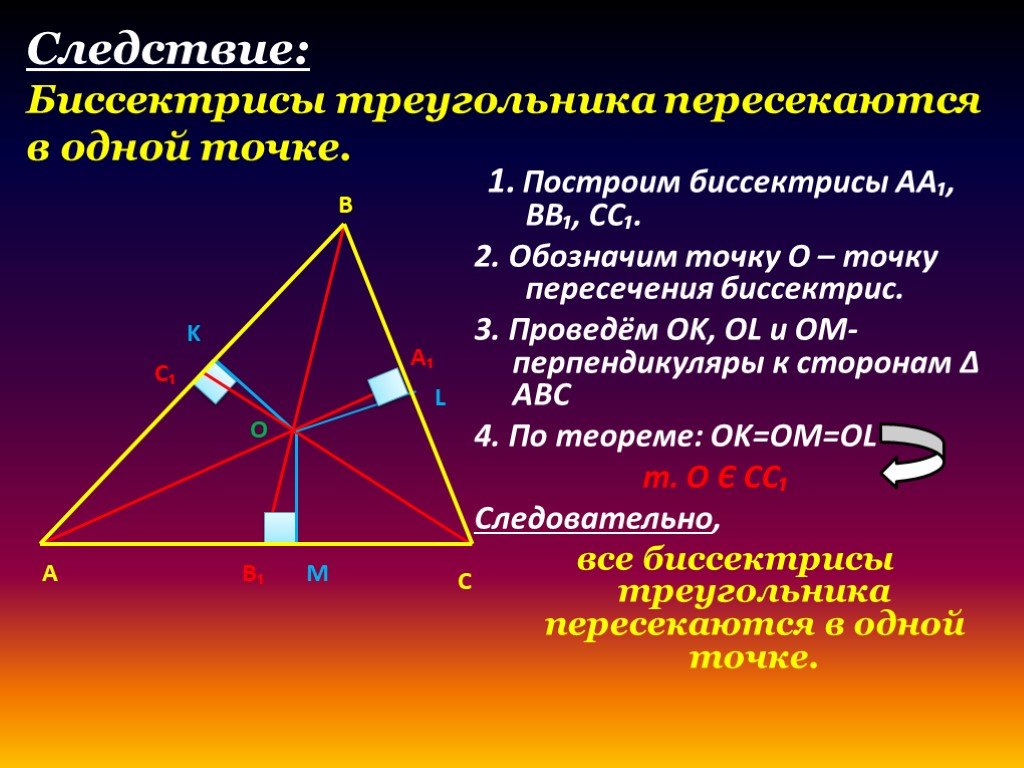
Ортоцентр может находиться как внутри, так и вне треугольника, в зависимости от его типа.
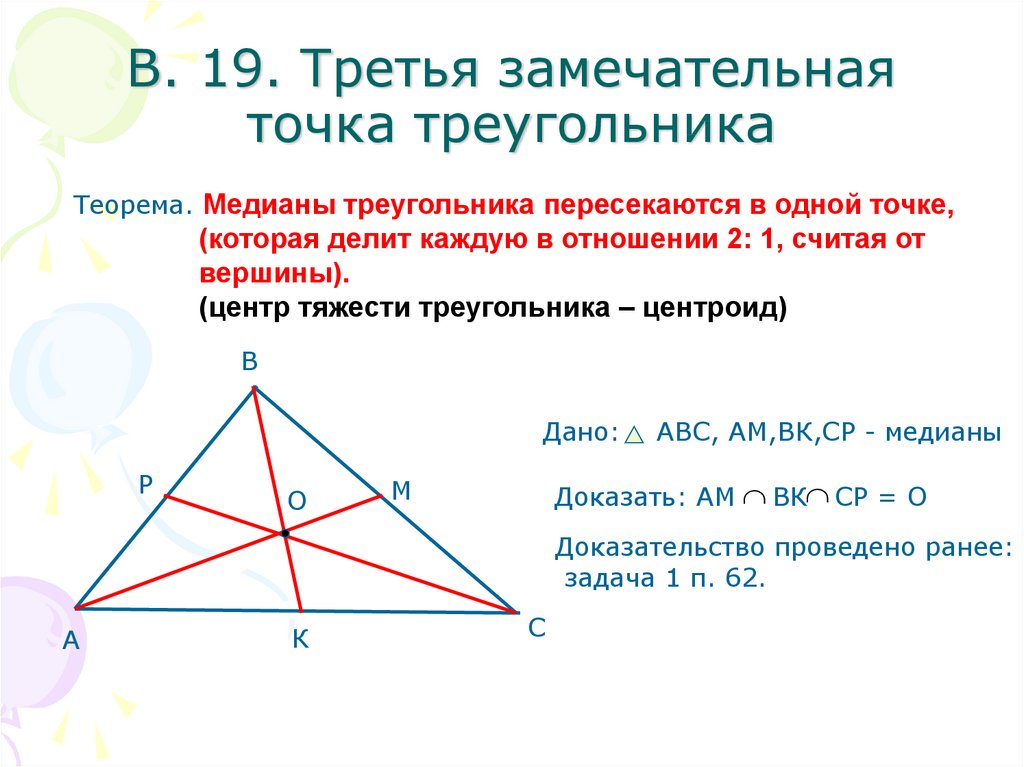
Медиана, биссектриса и высота треугольника. Геометрия 7 класс.
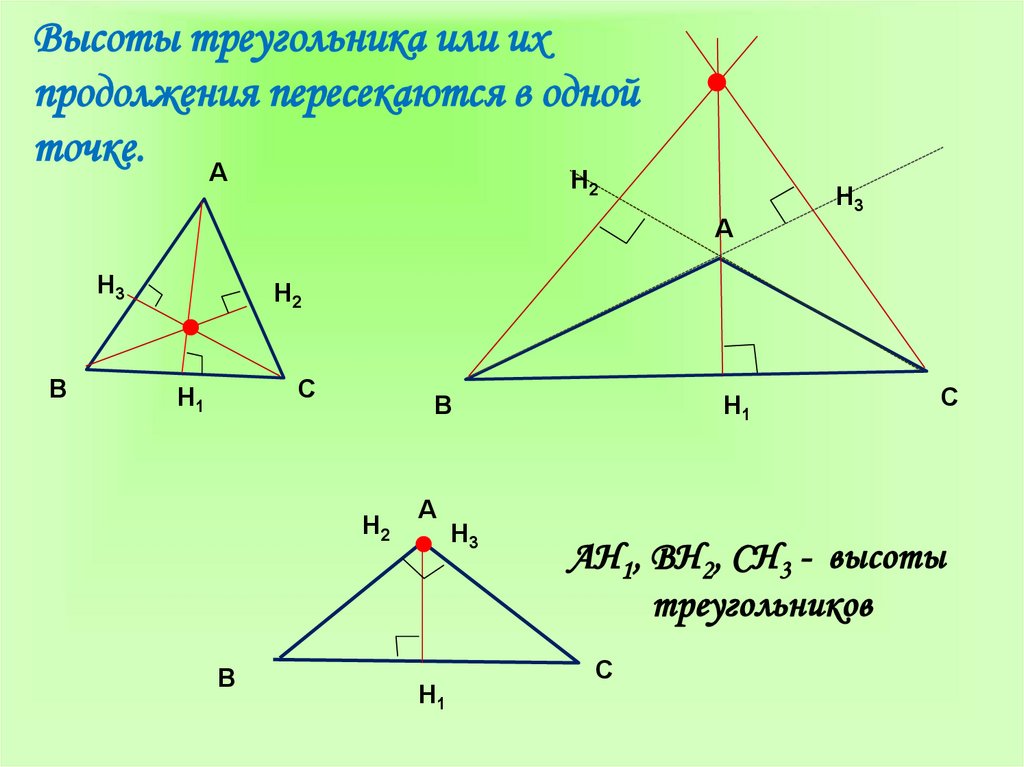
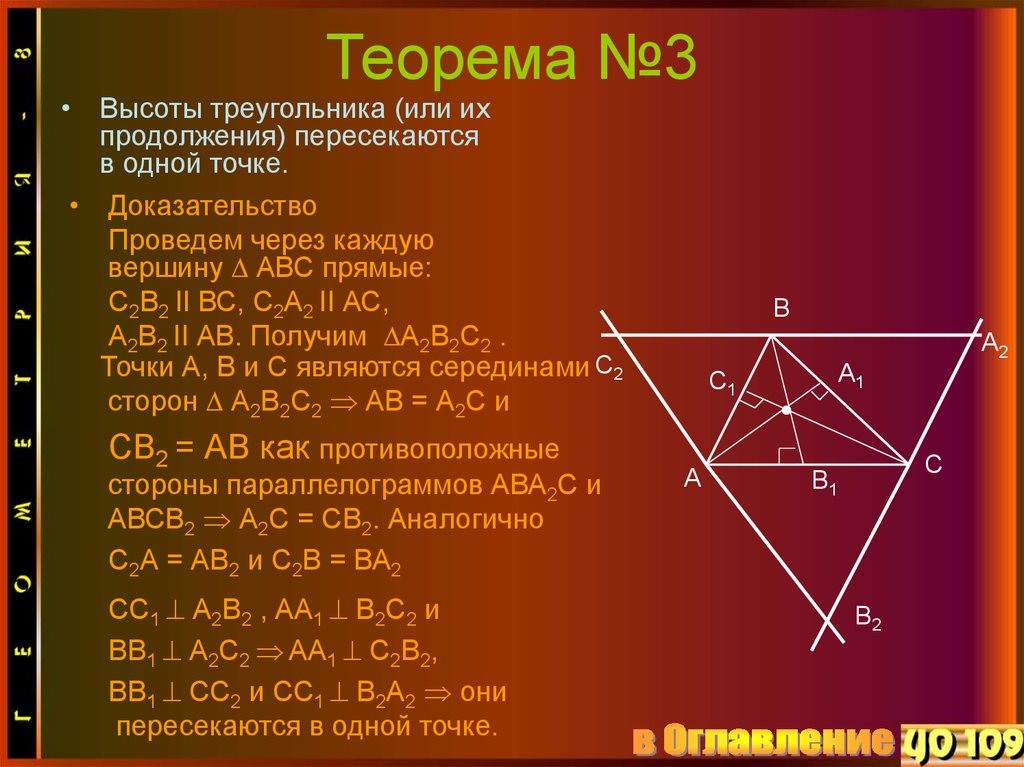
Высоты всегда пересекаются в одной точке независимо от типа треугольника.
При построении высоты используйте линейку и угольник для точности.
Высоты являются важными элементами в решении задач на площадь треугольника.

Высоты треугольника пересекаются в одной точке
Ортоцентр может быть использован для построения описанной окружности.

Новое доказательство пересечения высот треугольника в одной точке
Знание свойств высот треугольника полезно в тригонометрии и стереометрии.