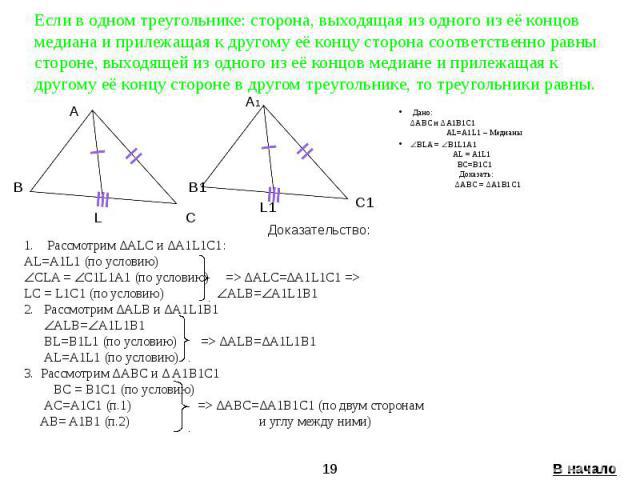
Медианы в равных треугольниках: Применение и свойства
Медианы в равных треугольниках играют важную роль в геометрии, помогая разделить треугольник на равные части и находить его центр тяжести. В этом руководстве мы рассмотрим, как правильно находить и применять медианы.

Для построения медианы в равном треугольнике найдите середину одной из его сторон.
Высота, биссектриса, медиана. 7 класс.

Соедините эту середину с противоположной вершиной треугольника.

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольника

Повторите процесс для всех сторон треугольника для нахождения всех медиан.
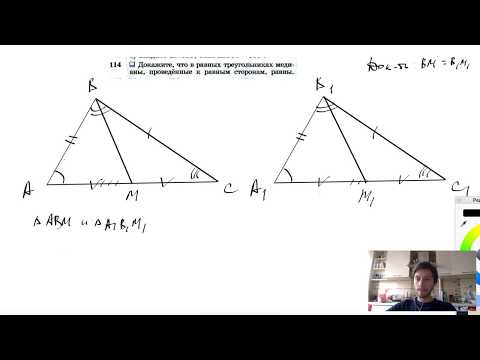
№114. Докажите, что в равных треугольниках медианы, проведенные к равным сторонам, равны.
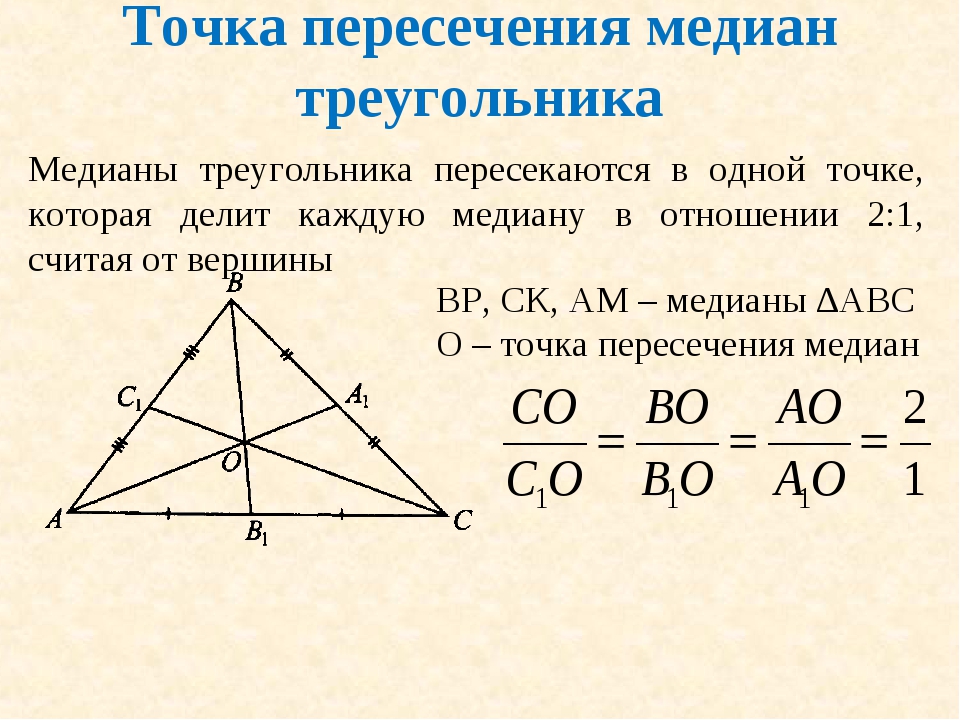
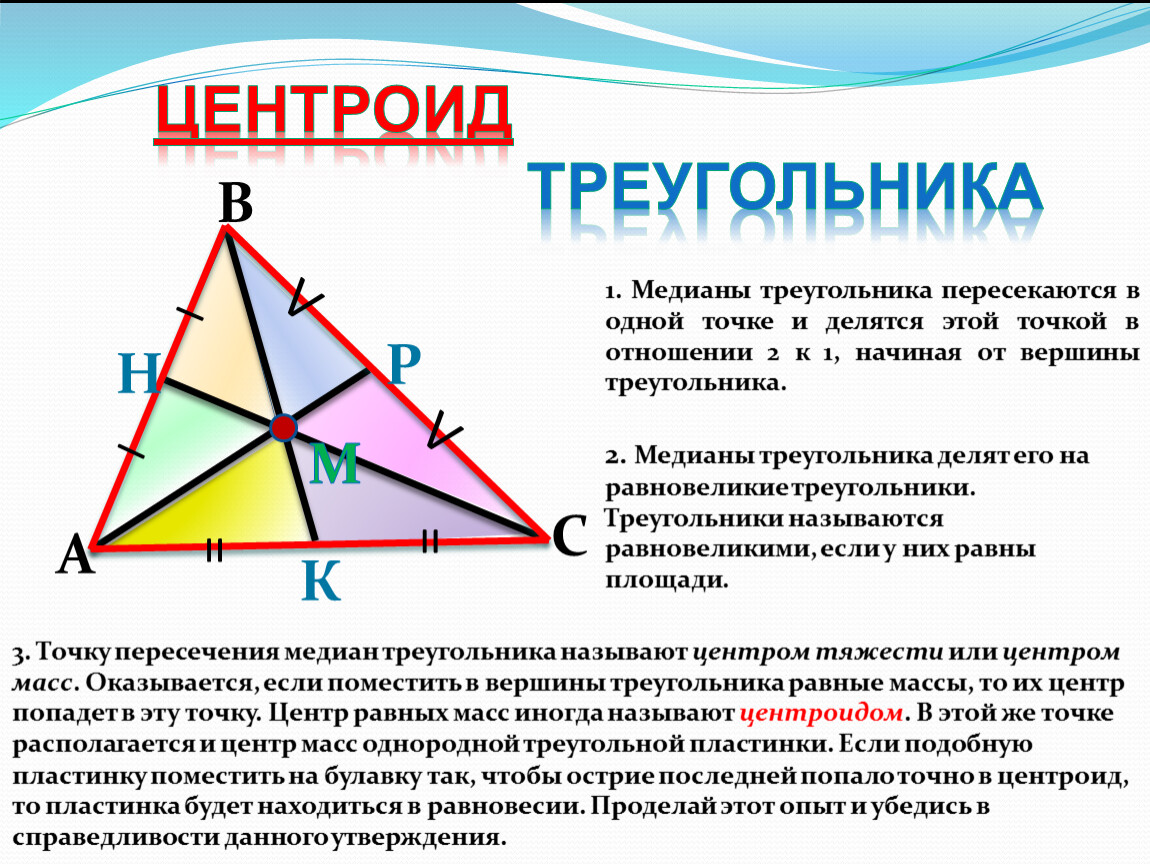
Медианы пересекаются в одной точке, которая называется центроидом треугольника.

Геометрия В треугольнике проведены три медианы. Докажите, что они разбивают треугольник на шесть
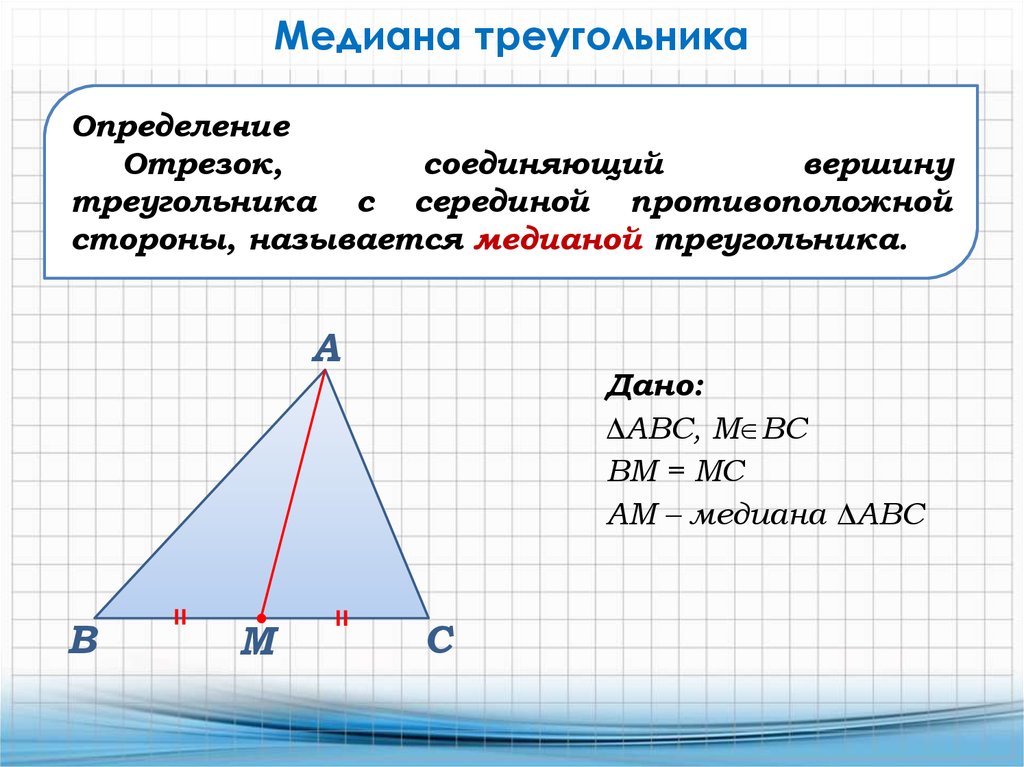
Центроид делит каждую медиану в соотношении 2:1, считая от вершины треугольника.

Геометрия Докажите, что в подобных треугольниках высоты, проведенные из вершины соответственных
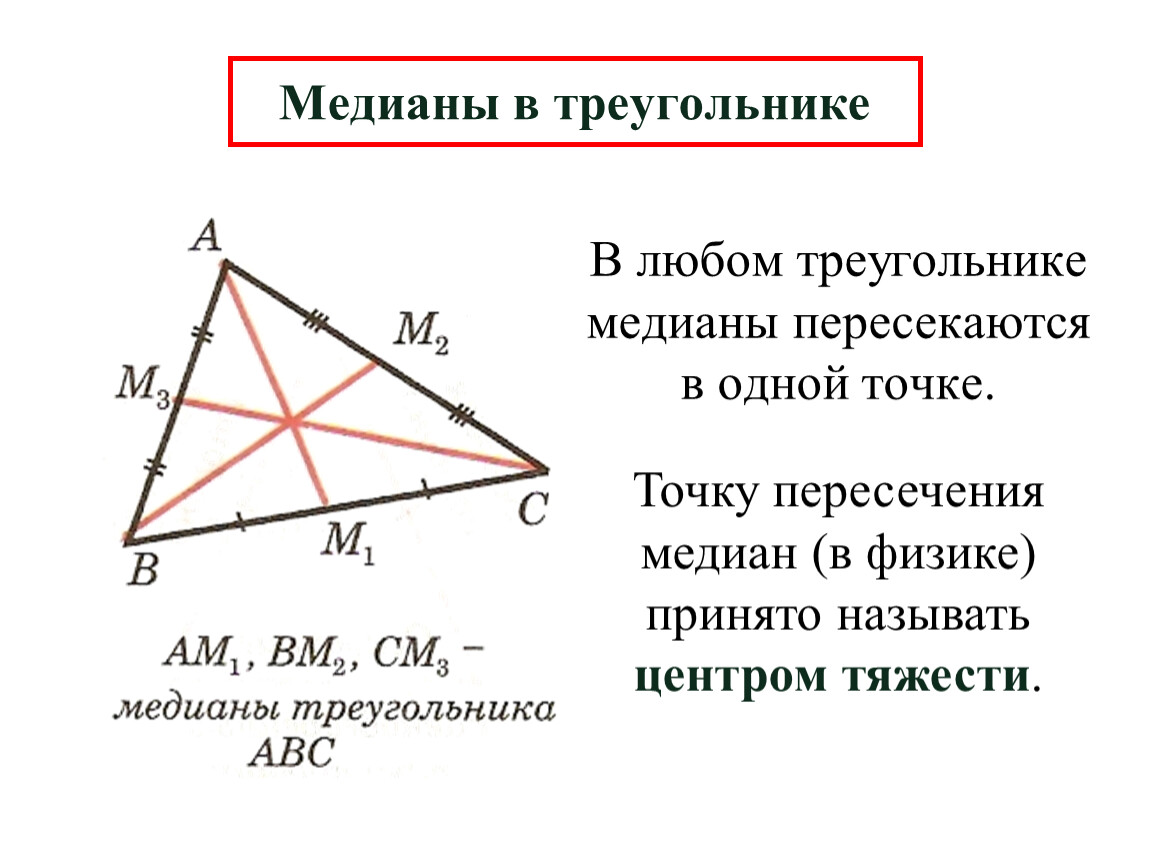
Используйте медианы для нахождения площади треугольника, если известны длины всех сторон.

Геометрия 7. Треугольники. Медиана и биссектриса треугольника. Определение и свойства. Решение задач

Построение медиан может помочь в решении задач на нахождение площади и центра тяжести треугольника.
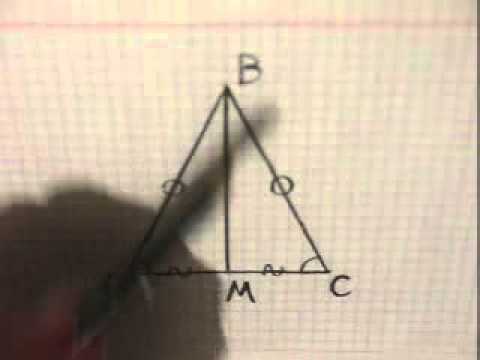
Теорема о свойстве медианы равнобедренного треугольника
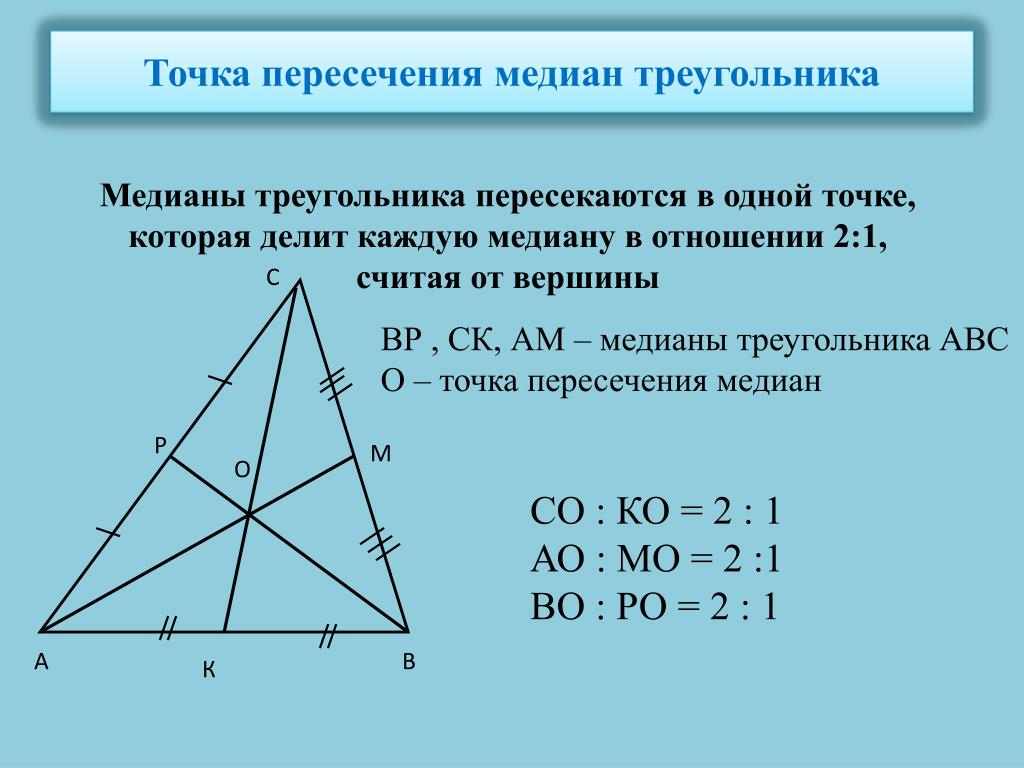
При построении медиан используйте линейку и циркуль для точных измерений.

Задание 25 Равнобедренный треугольник Равенство медиан

8. Медиана треугольника и её свойства.
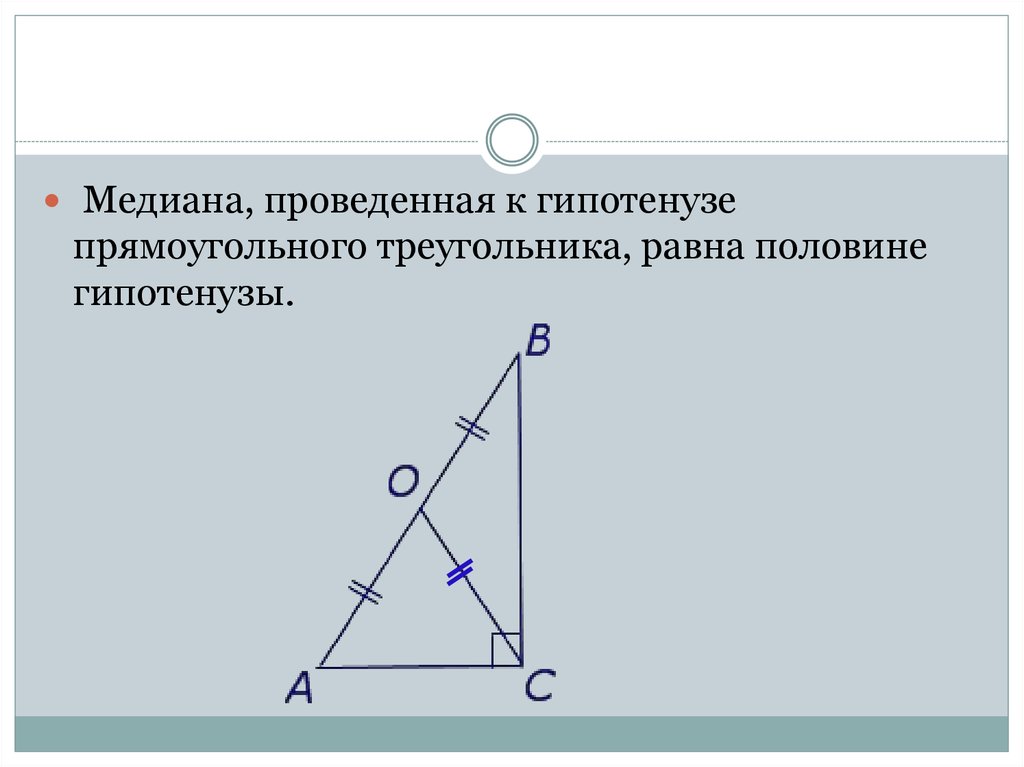
Помните, что медиана делит треугольник на два треугольника равной площади.
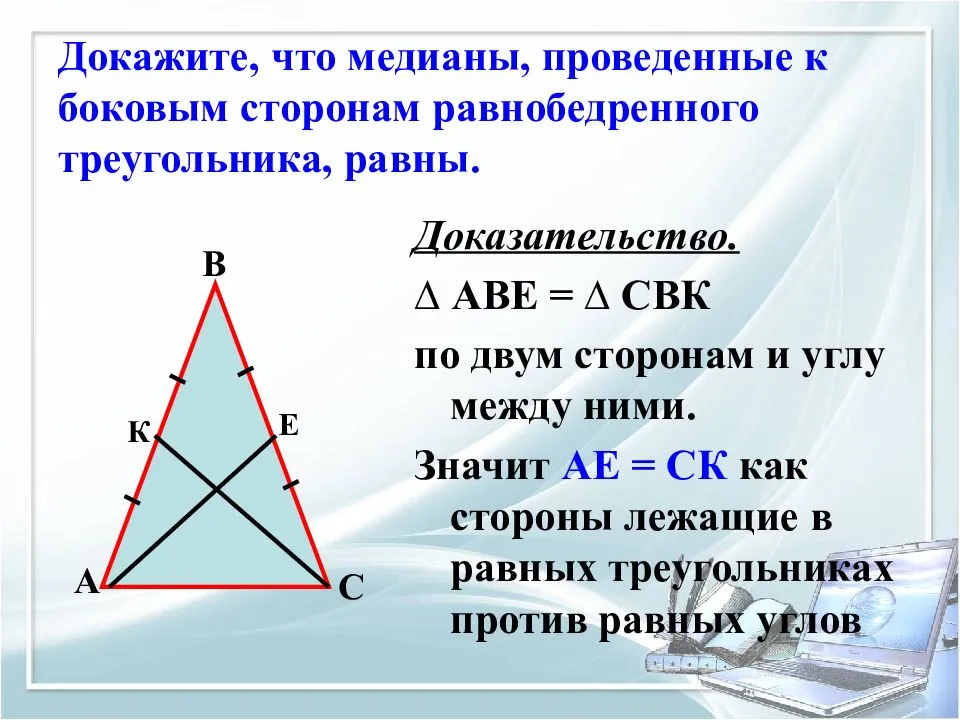
Для проверки правильности построения медиан используйте геометрические программы или приложения.
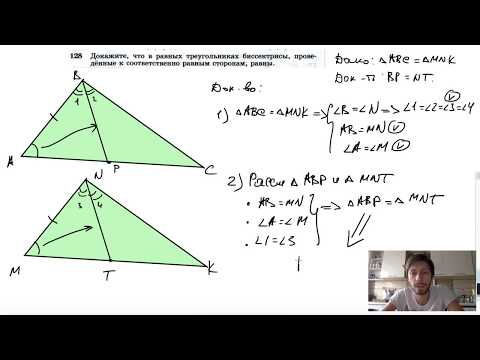
№128. Докажите, что в равных треуголь