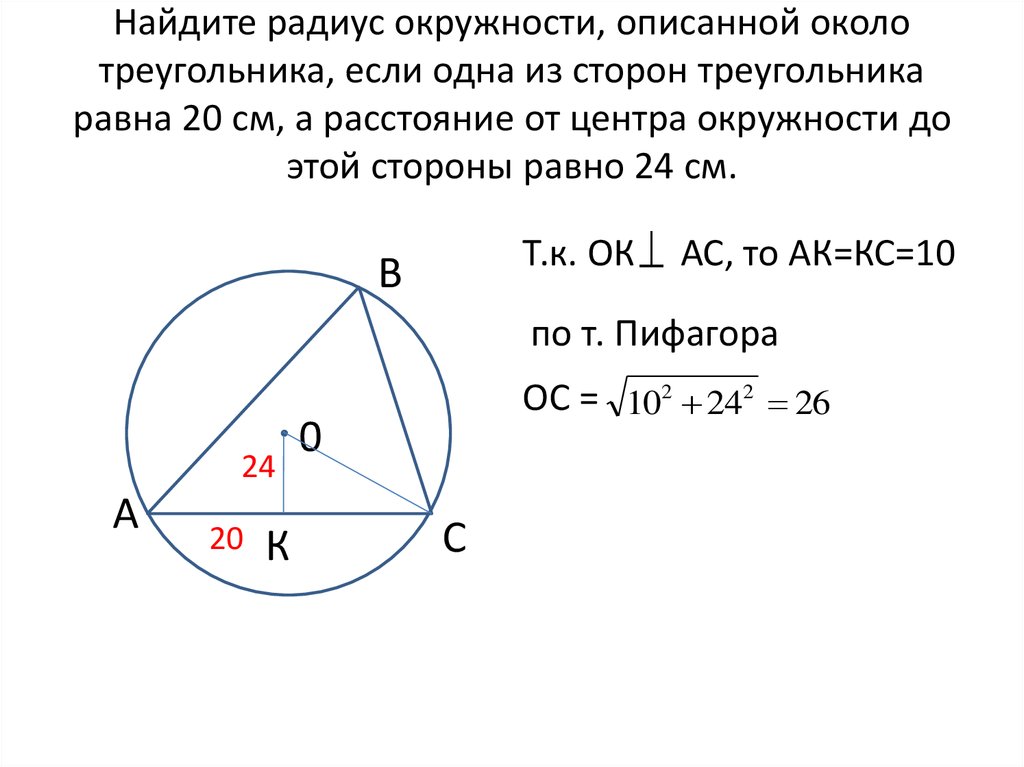
Методы нахождения стороны треугольника через описанную окружность
На этой странице вы найдете полезные советы и пошаговые инструкции по вычислению стороны треугольника, описанного вокруг окружности. Мы расскажем, какие формулы и методы можно использовать для нахождения длины стороны, учитывая параметры окружности и треугольника.
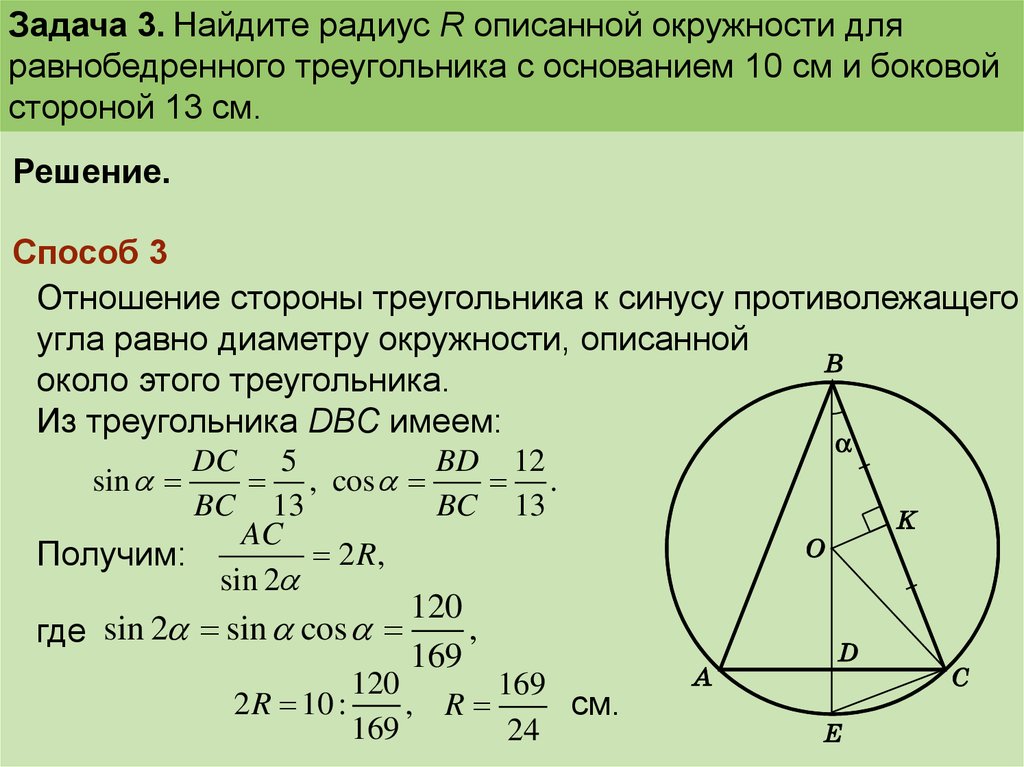
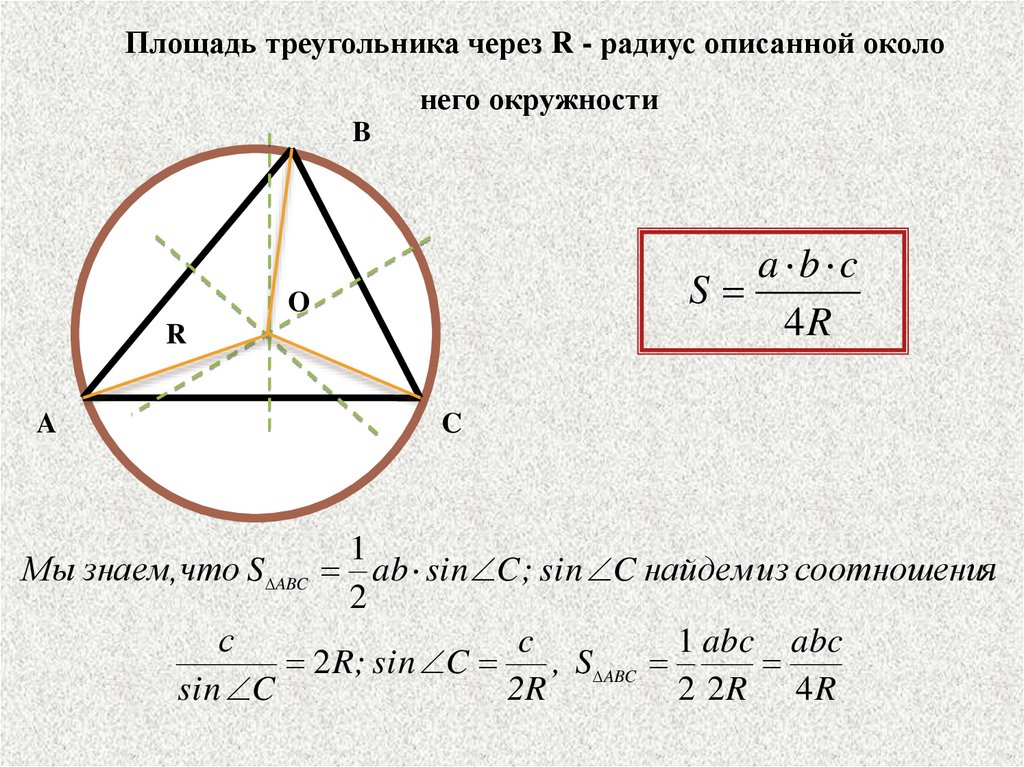
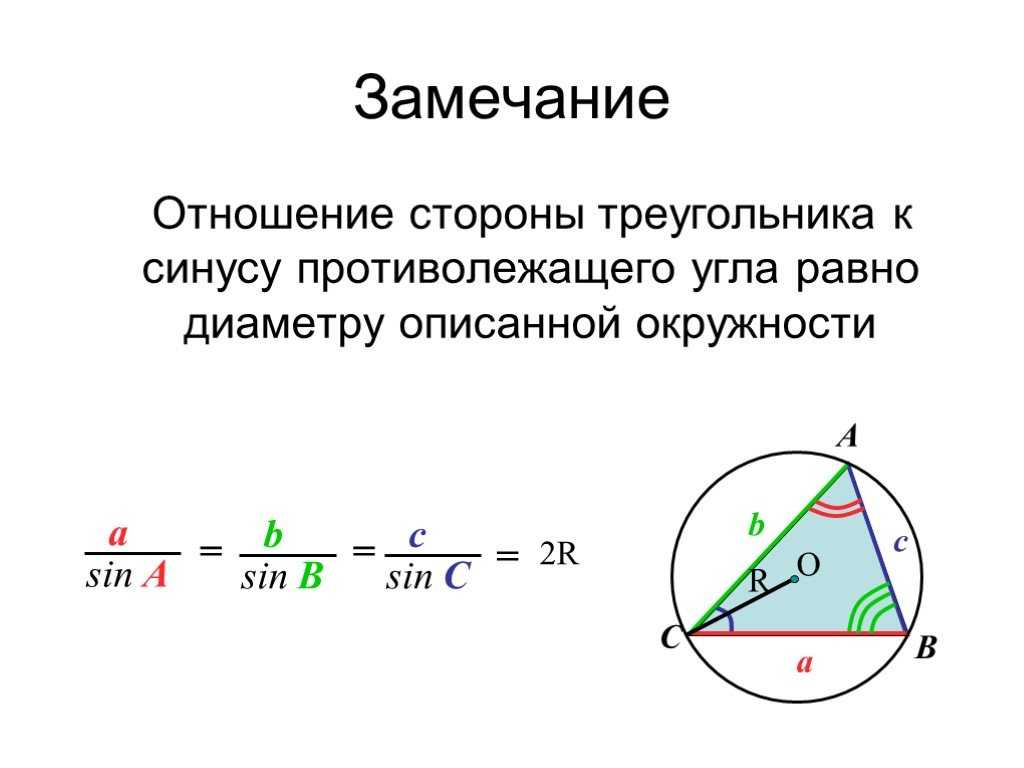
Для вычисления стороны треугольника, описанного вокруг окружности, используйте формулу a=2Rsin(A)a = 2R/sin(A)a=2Rsin(A), где RRR — радиус окружности, а AAA — угол, противолежащий стороне aaa.

Окружность вписанная в треугольник и описанная около треугольника.
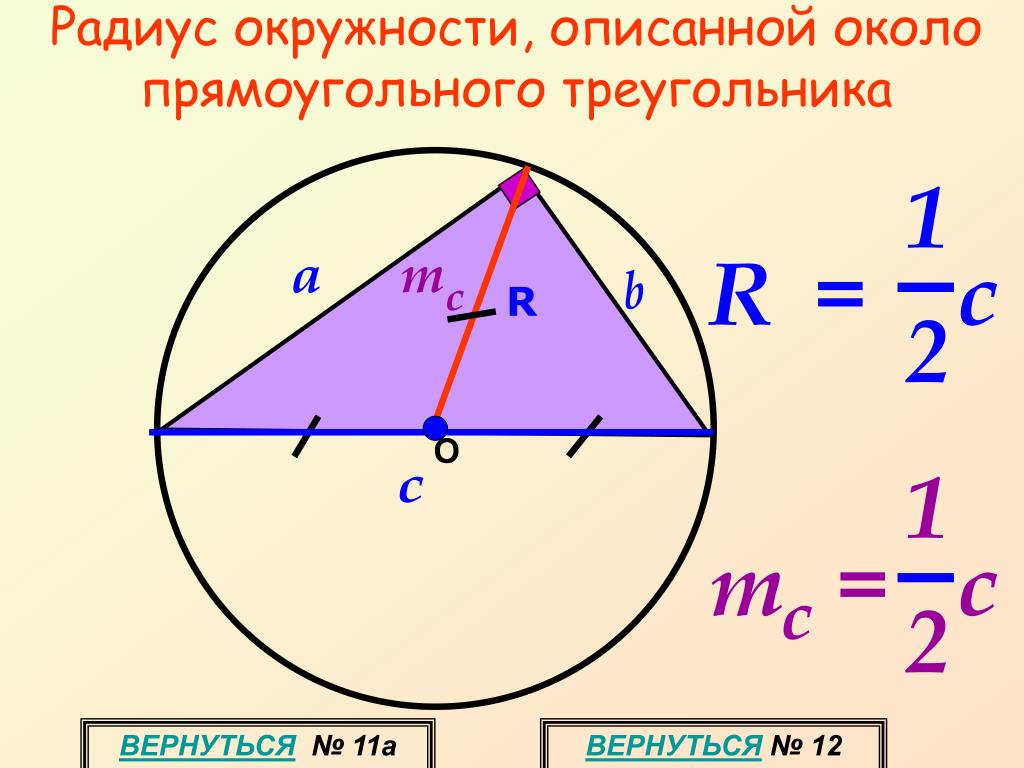

Помните, что все углы треугольника, описанного вокруг окружности, должны быть острыми, иначе правильное вычисление невозможно.

Построить описанную окружность (Задача 1)
Если известен радиус окружности и один угол треугольника, можно легко найти все стороны, зная, что сумма всех углов треугольника равна 180 градусам.
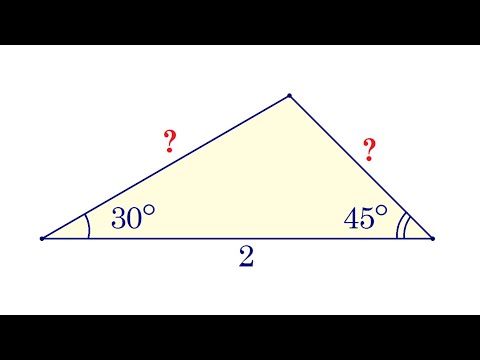
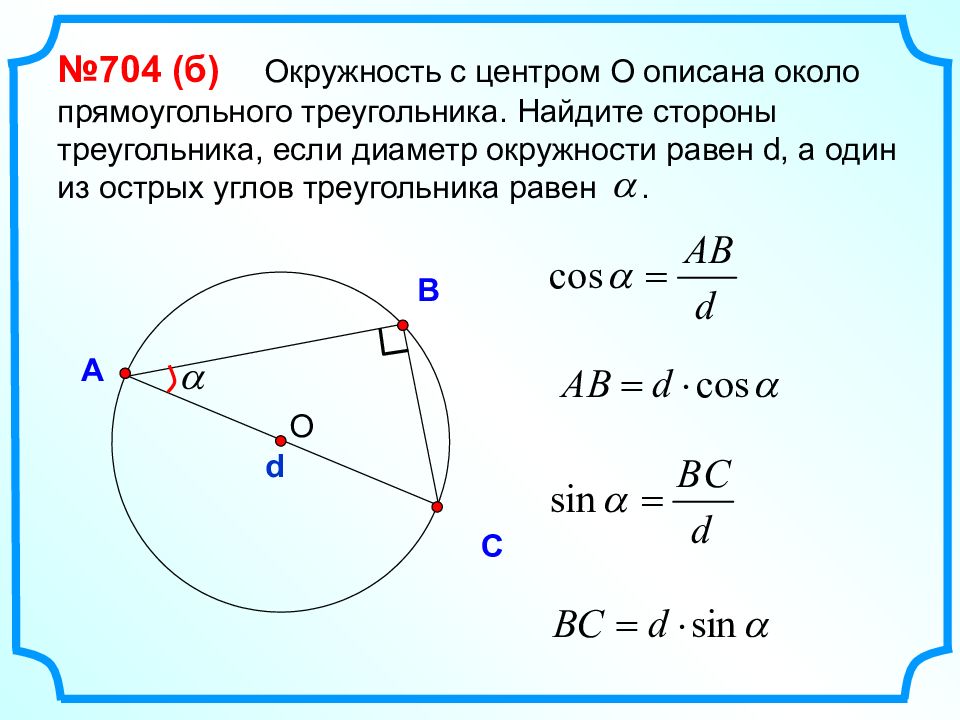
По силам каждому ★ Найдите стороны треугольника на рисунке

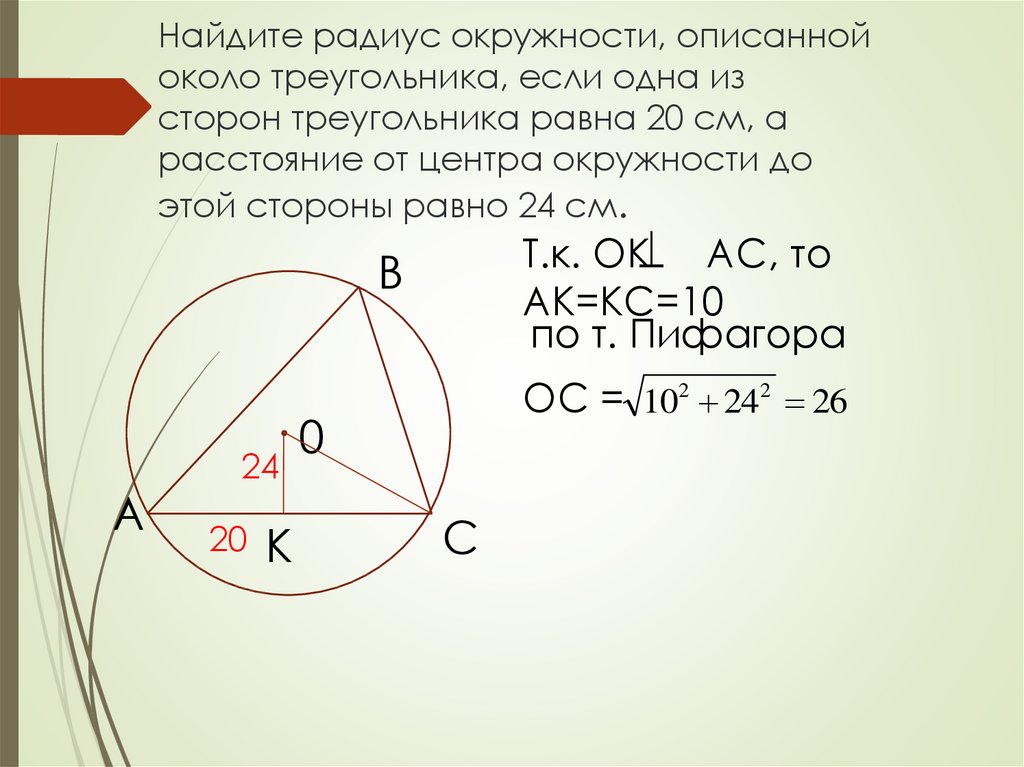
При наличии информации о радиусе окружности и одной стороне треугольника используйте теорему синусов для нахождения остальных сторон.

Найдите площадь треугольника на рисунке ★ Два способа решения

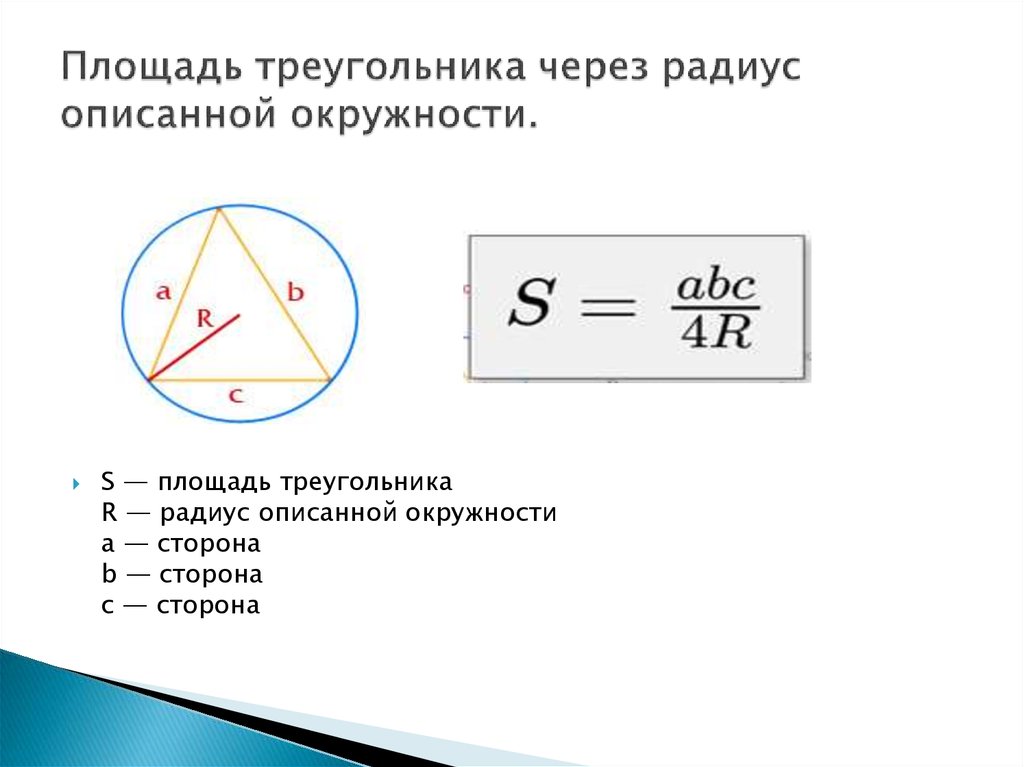
Используйте формулы площади треугольника для проверки правильности вычислений. Площадь можно найти через радиус описанной окружности и длину сторон.
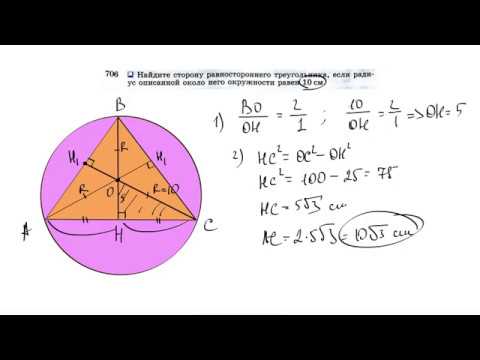
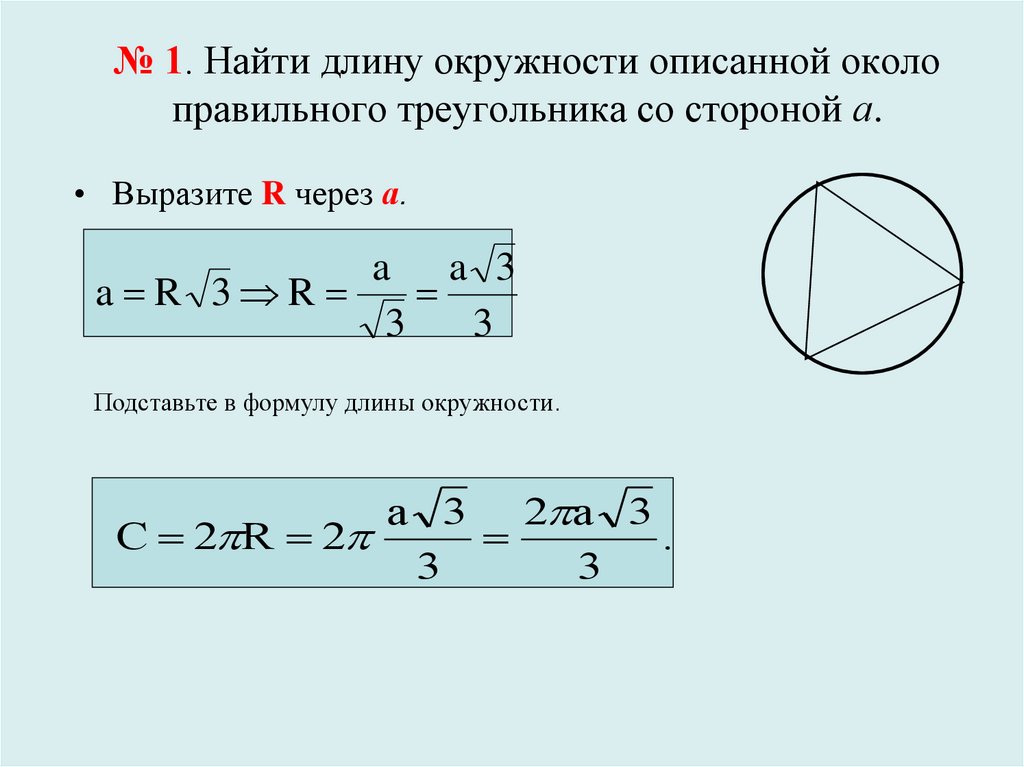
№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружности

Для треугольников с известными сторонами и радиусом описанной окружности применяйте формулу Герона для нахождения площади, а затем используйте ее для проверки длины сторон.

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.
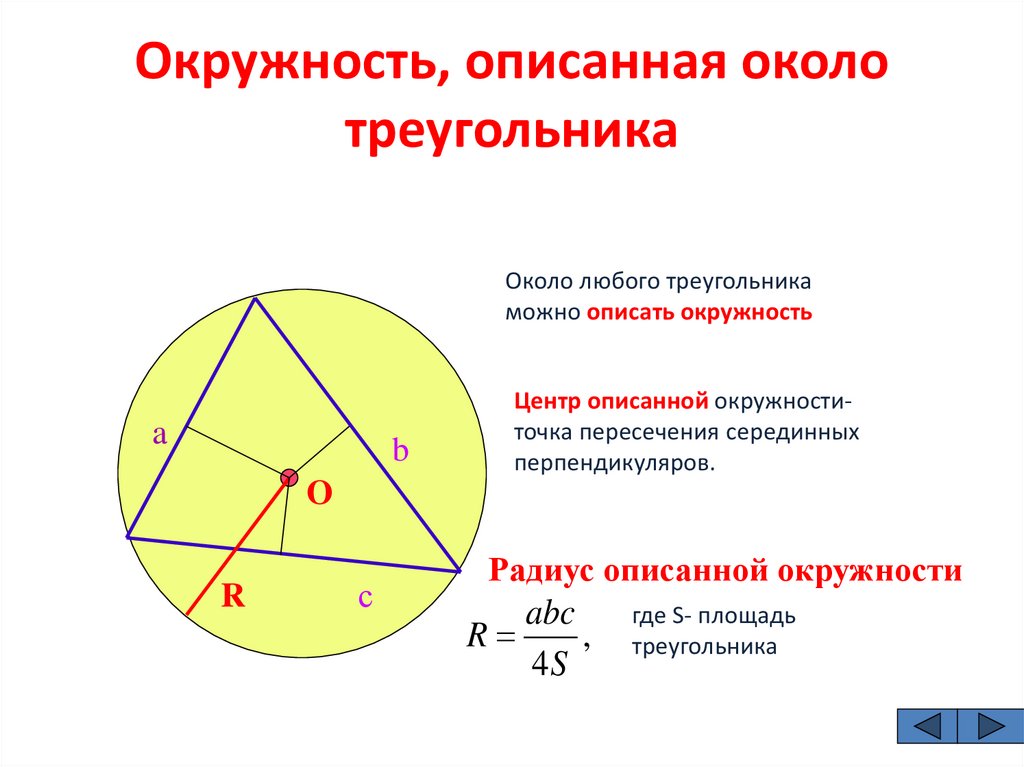
Если известны все три стороны треугольника, вычислить радиус описанной окружности можно через формулу R=abc4SR = /frac{abc}{4S}R=4Sabc, где aaa, bbb, ccc — стороны треугольника, а SSS — его площадь.

Вписанная и описанная окружности - Лайфхак для запоминания
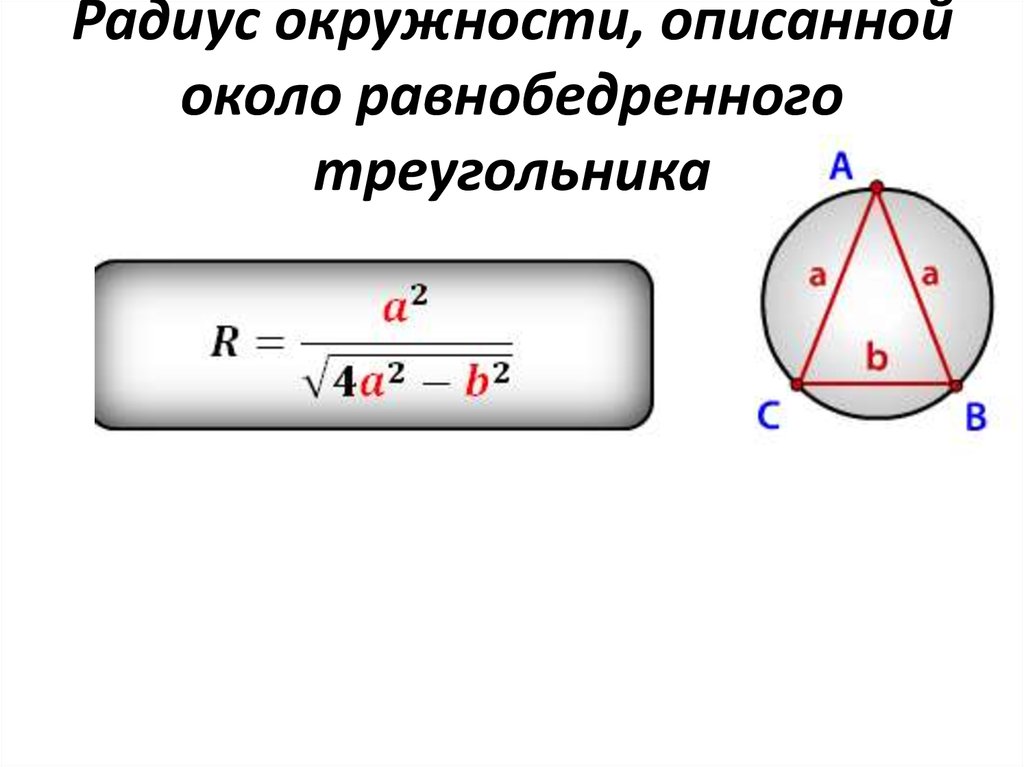
Для равностороннего треугольника радиус описанной окружности равен R=a3R = /frac{a}{/sqrt{3}}R=3a, где aaa — сторона треугольника.

Как творчество помогает реализовать цели и исполнить мечты - Алексей Романоф

Власть циничной горстки людей над абсолютно циничным народом. Владимир Буковский о России.
При решении задач старайтесь использовать более простые числовые примеры, чтобы облегчить вычисления и избежать ошибок.
Всегда проверяйте полученные результаты, используя различные методы и формулы, чтобы удостовериться в их правильности.