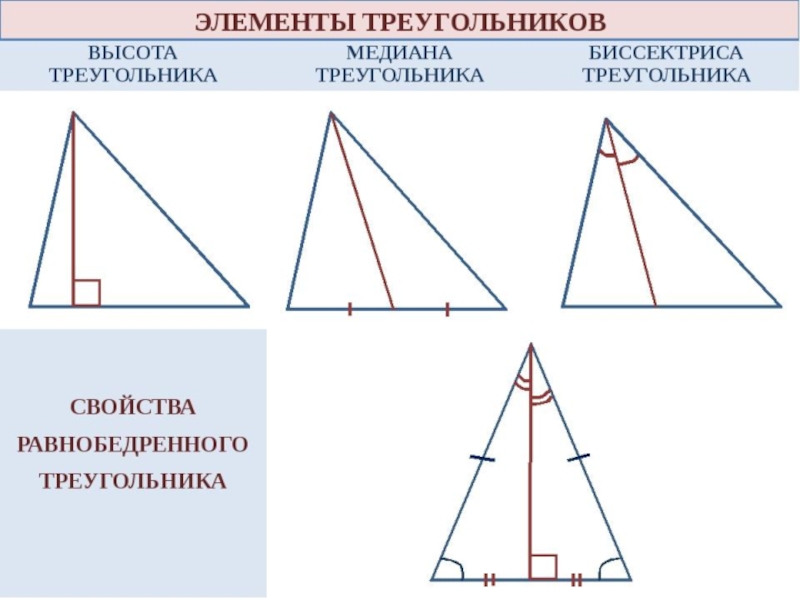
Основные элементы геометрии треугольника: медианы, биссектрисы и высоты

В этой статье вы найдете подробное объяснение ключевых понятий геометрии треугольника, таких как медианы, биссектрисы и высоты. Эти элементы играют важную роль в различных расчетах и свойствах треугольников, и их понимание является основой для многих задач и теорем.

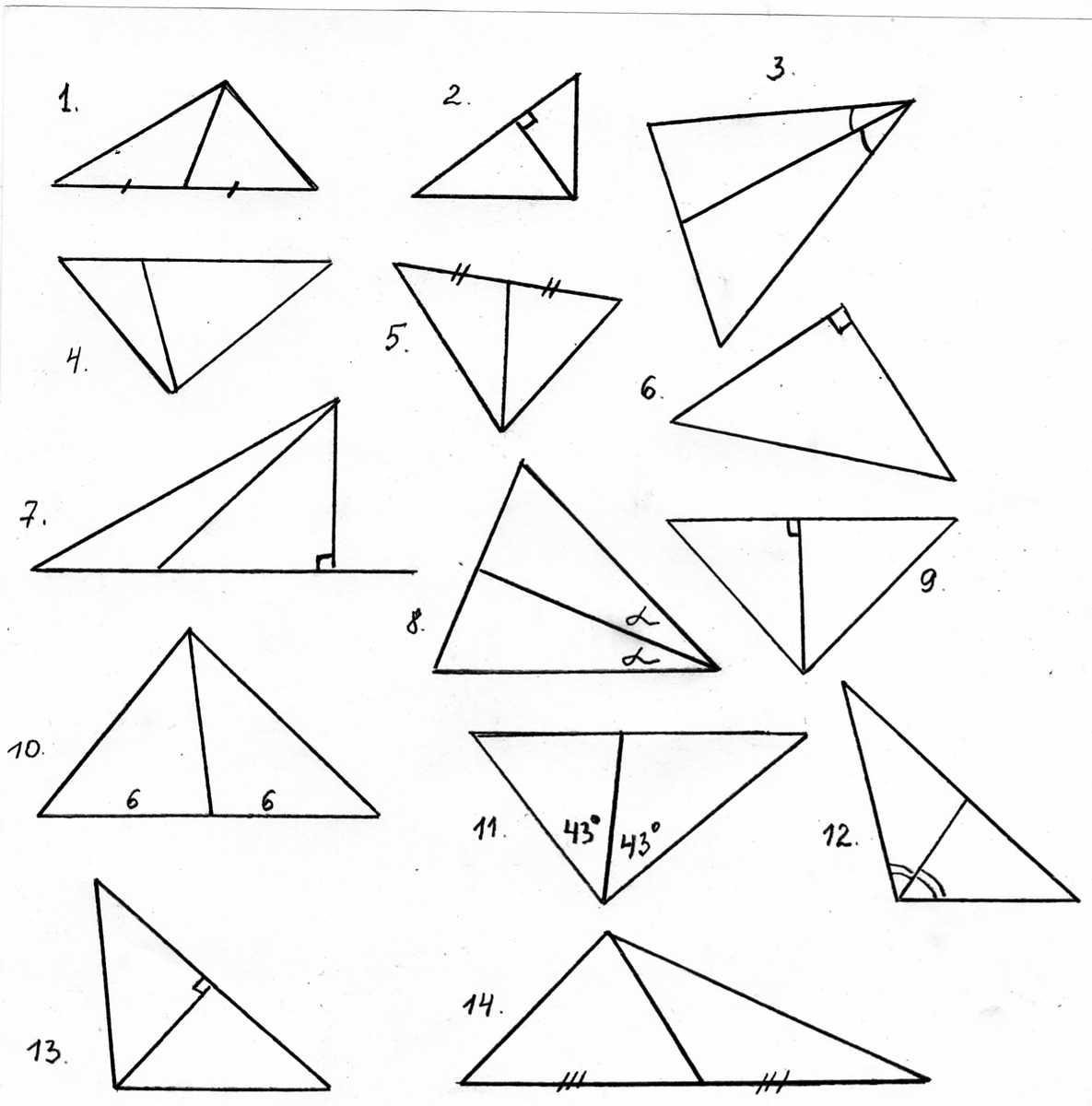
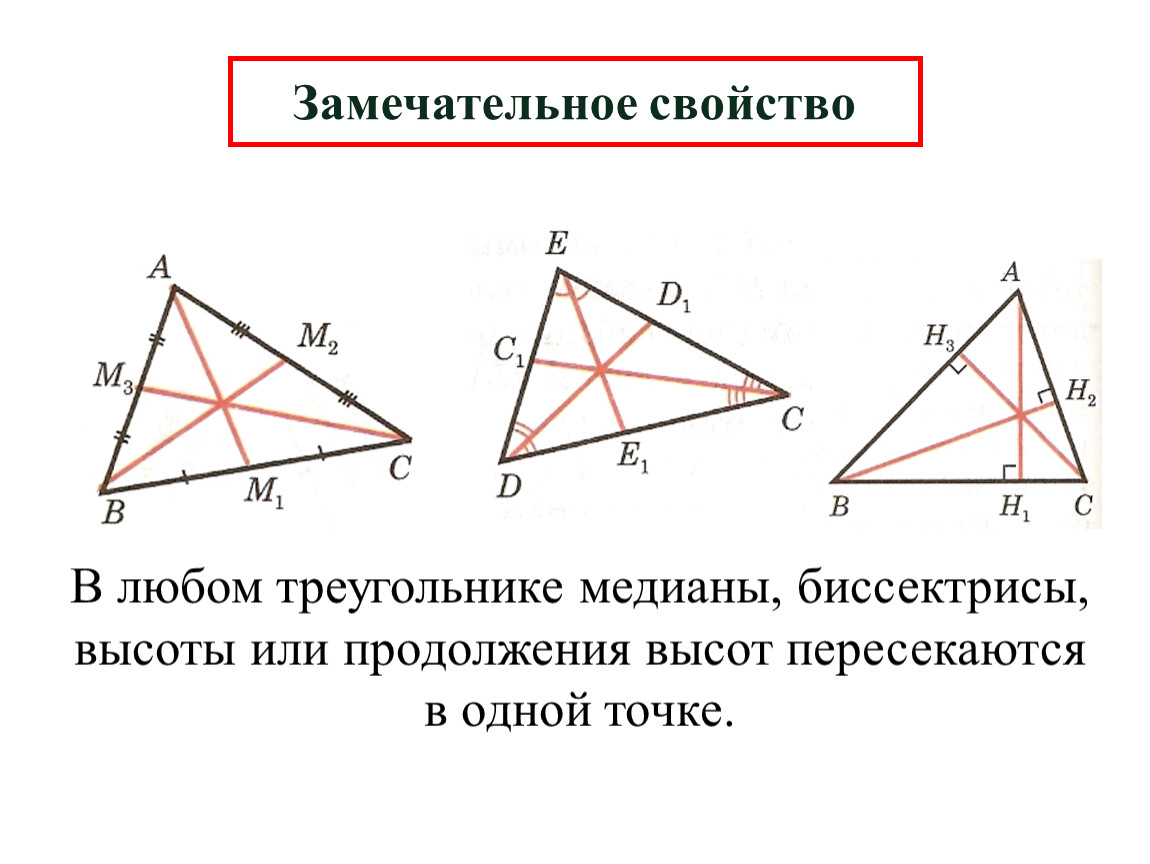
При работе с треугольниками всегда проверяйте, что все медианы пересекаются в одной точке — это центр масс треугольника.

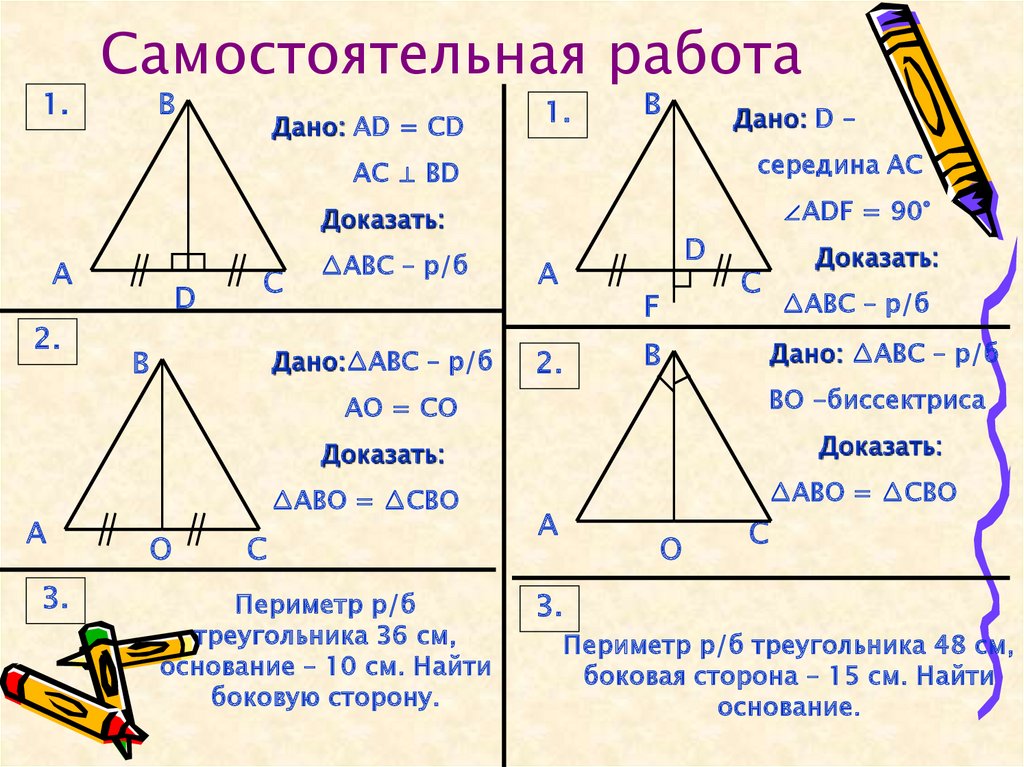
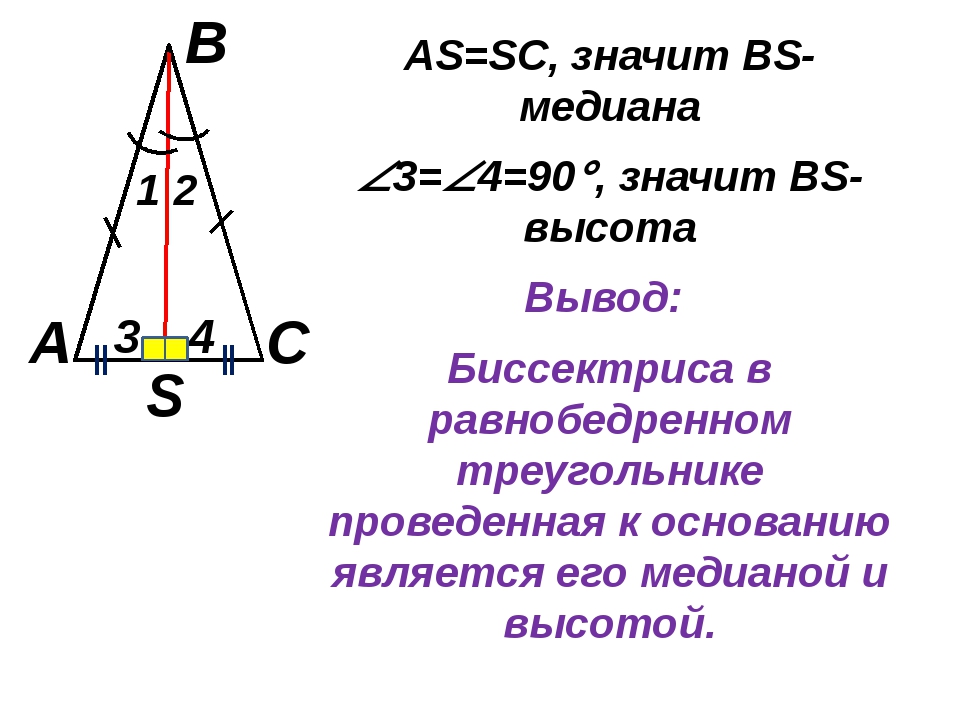
Биссектрисы треугольника всегда пересекаются в одной точке, которая называется инцентр, и от этой точки можно провести радиус окружности, вписанной в треугольник.

Не забудьте, что высоты треугольника пересекаются в одной точке, которая называется ортоцентром. Это свойство полезно при решении задач, связанных с углами треугольника.

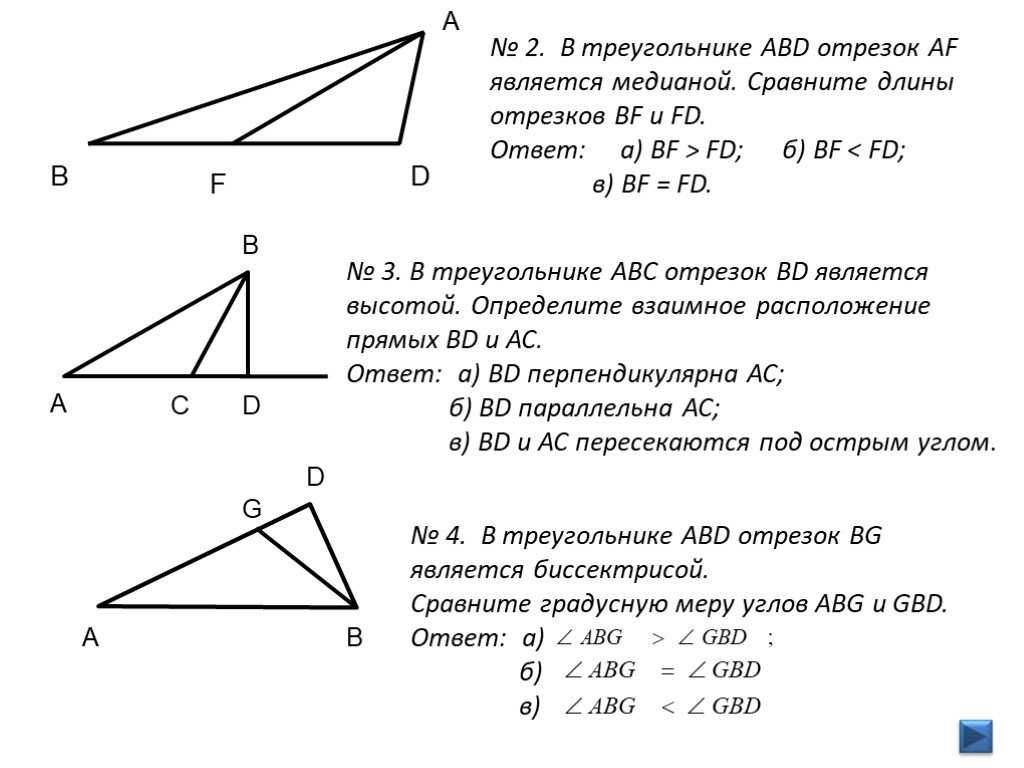
Используйте свойства медиан для упрощения вычислений: медиана делит треугольник на два треугольника с равными площадями.

Знайте, что биссектрисы делят углы треугольника в пропорции длины прилегающих сторон, что может быть полезно при решении задач на подобие треугольников.

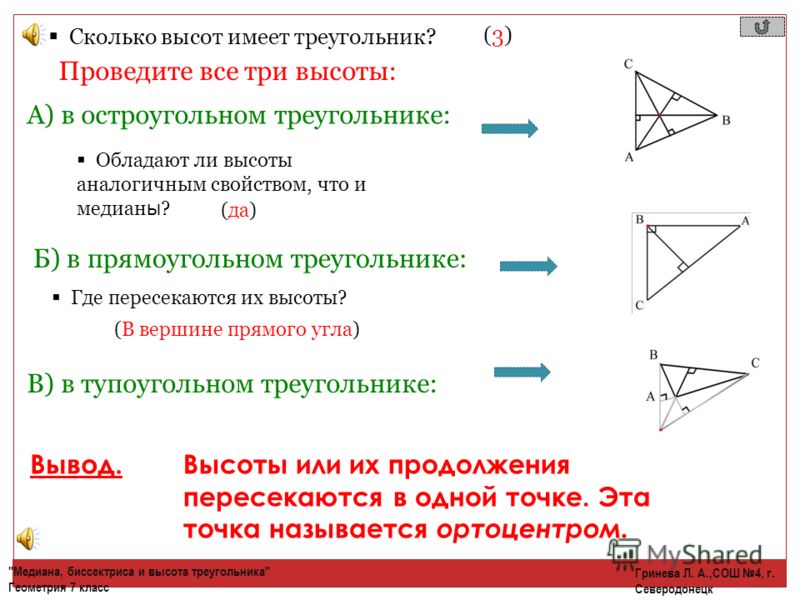
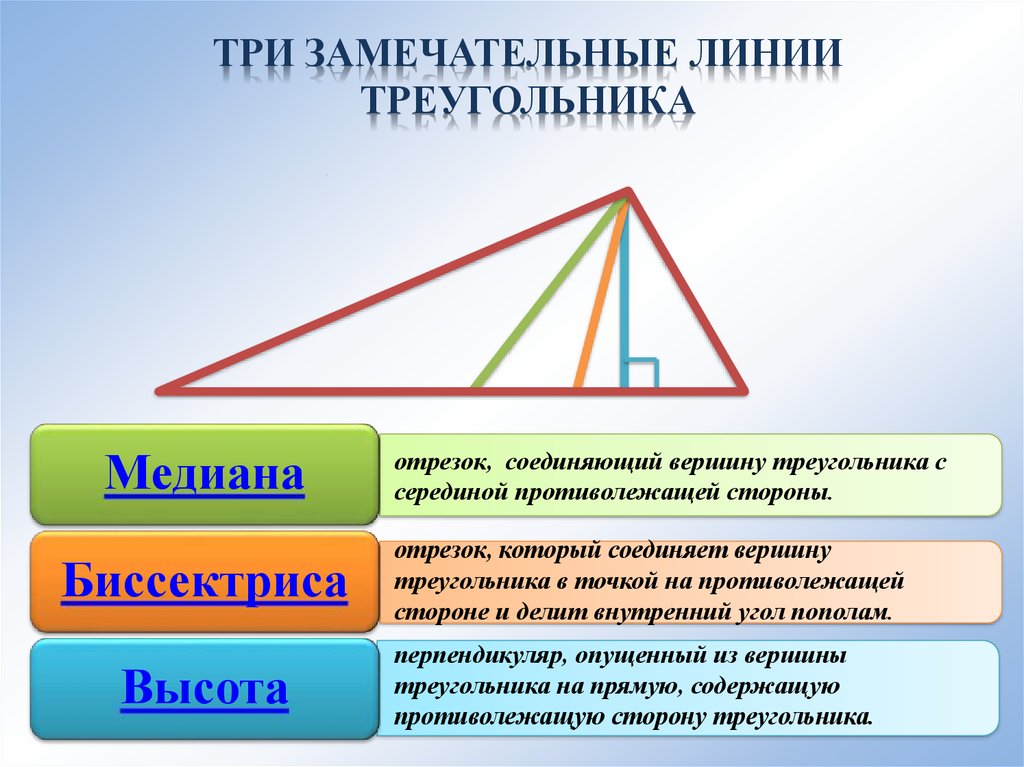
Ориентируйтесь на свойства ортоцентра: он может находиться внутри или за пределами треугольника в зависимости от его типа (остроугольный, прямоугольный или тупоугольный).

Понимание соотношений высот и медиан может помочь в нахождении элементов треугольника, таких как его периметр и площадь.

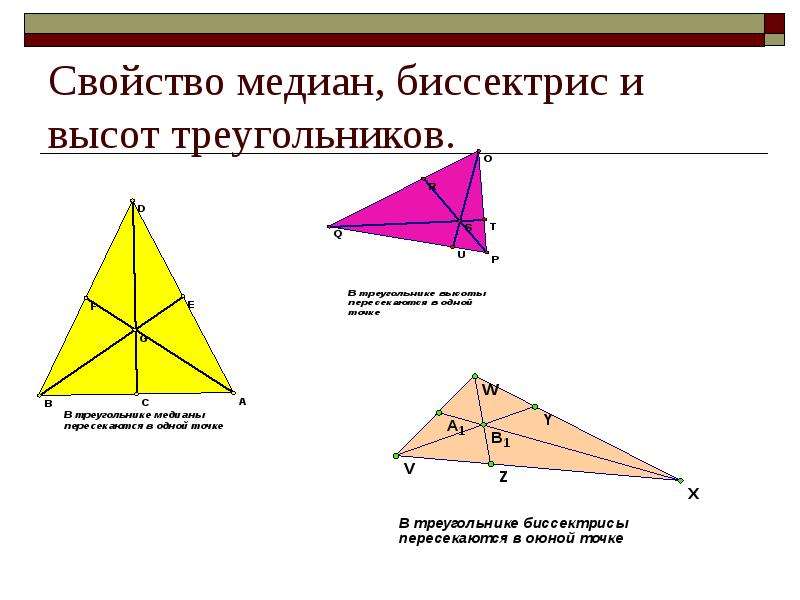
Для упрощения задач по треугольникам полезно запомнить стандартные формулы, связанные с медианами и высотами.

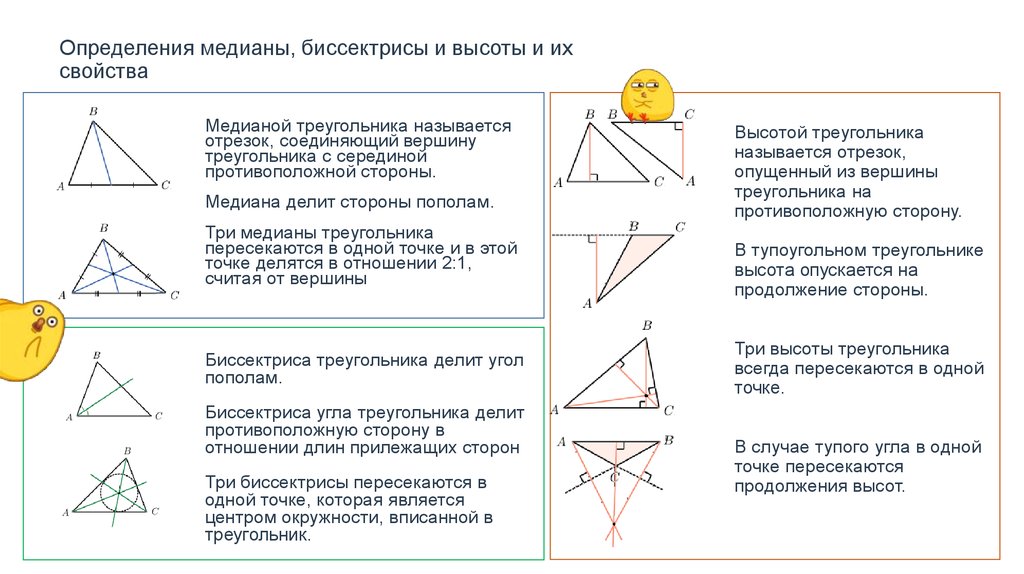
При вычислении длины медианы используйте теорему о медианах, чтобы упростить расчеты, особенно в сложных треугольниках.

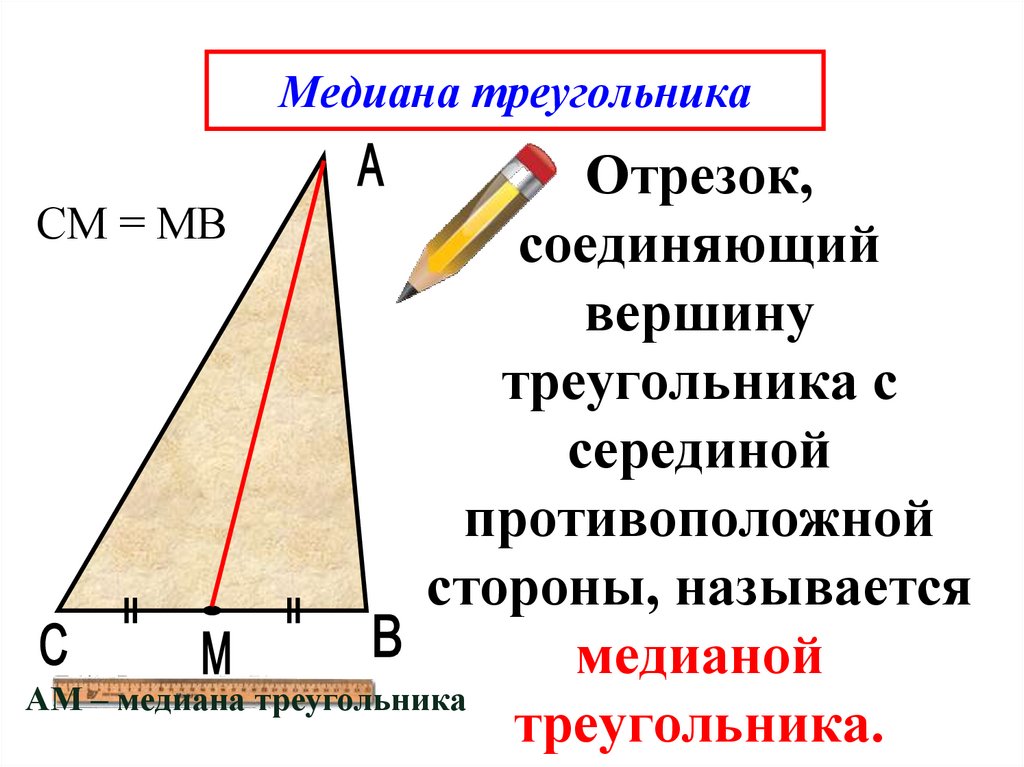
Используйте диаграммы и чертежи для наглядного представления медиан, биссектрис и высот треугольника, чтобы лучше понять их взаимное расположение.